Giải Toán 6 Bài 3: Phép cộng và phép trừ hai số nguyên - Chân trời sáng tạo
Lời giải bài tập Toán lớp 6 Bài 3: Phép cộng và phép trừ hai số nguyên sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6.
A. Câu hỏi trong bài
Toán lớp 6 trang 57 Hoạt động khởi động
Làm thế nào để tìm được tổng của hai số nguyên?
Lời giải:
Sau bài học ngày hôm nay, để tính tổng của hai số nguyên, ta làm như sau:
Muốn cộng hai số nguyên cùng dấu, ta làm như sau:
Muốn cộng hai số nguyên dương, ta cộng chúng lại như số tự nhiên.
Muốn cộng hai số nguyên âm, ta cộng hai số đối của chúng rồi thêm dấu trừ đằng trước kết quả.
Muốn cộng hai số nguyên trái dấu, ta làm như sau:
Nếu hai số nguyên đối nhau thì tổng bằng 0.
Nếu số dương lớn hơn số đối của số âm thì ta lấy số dương trừ đi số đối của số âm.
Nếu số dương bé hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ trước kết quả.
Toán lớp 6 trang 57 Hoạt động khám phá 1
Lời giải:
a) Người đó di chuyển từ số 0 sang bên phải 2 đơn vị, sau đó lại tiếp tục di chuyển sang bên phải ba đơn vị thì người đó dừng tại điểm 5.
Khi đó, ta có: (+2) + (+3 )= (+5).
b) Người đó di chuyển từ số 0 sang bên trái 2 đơn vị, sau đó di chuyển tiếp về bên trái 3 đơn vị thì người đó dừng lại tại điểm – 5.
Khi đó, ta có: (-2) + (-3) = (-5).
Ta có tổng 2 + 3 = 5.
Số đối của tổng này là – 5.
Do đó (-2) + (-3) = - (2 + 3) = (-5).
Toán lớp 6 trang 58 Thực hành 1
Lời giải:
a) 4 + 7 = 11;
b) (-4) + (-7) = - (4 + 7) = -11;
c) (-99) + (-11) = - (99 + 11) = -110;
d) (+99) + (+11) = 99 + 11 = 110;
e) (-65) + (-35) = - (65 + 35) = -100.
Toán lớp 6 trang 58 Vận dụng 1
Lời giải:
Bác Hà nợ bác Lan 80 nghìn đồng được biểu diễn là: - 80 (nghìn đồng).
Bác Hà nợ tiếp bác Lan 40 nghìn đồng được biểu diễn là: - 40 (nghìn đồng).
Tổng số tiền bác Hà nợ bác Lan là: (-80) + (-40) = - (80 + 40) = -120 (nghìn đồng).
Toán lớp 6 trang 58 Hoạt động khám phá 2
Lời giải:
a) Người đó dừng lại tại điểm 0.
Kết quả của phép tính: (+4) + (-4) = 0.
b) Người đó dừng lại tại điểm 0.
Kết quả của phép tính: (-4) + (+4) = 0.
Toán lớp 6 trang 58 Vận dụng 2
Lời giải:
Thẻ tín dụng đang ghi nợ 2 000 000 đồng được biểu diễn là: - 2 000 000 (đồng).
Bác Tám nộp vào tài khoản 2 000 000 đồng được biểu diễn là: + 2 000 000 (đồng).
Số tiền bác Tám có trong tài khoản là: (+ 2 000 000) + (-2 000 000) = 0 (đồng).
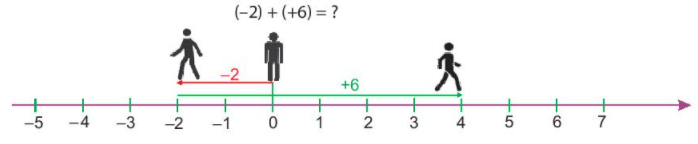
Toán lớp 6 trang 59 Hoạt động khám phá 3
Lời giải:
a) Người đó dừng lại tại điểm + 4.
Kết quả của phép tính: (-2) + (+6) = +4.
b) Người đó dừng lại tại điểm – 4.
Kết quả của phép tính: (+2) + (-6) = - 4.
Toán lớp 6 trang 60 Thực hành 2
Lời giải:
a) 4 + (-7) = - (7 – 3) = - 3
b) (-5) + 12 = 12 – 5 = 7
c) (-25) + 72 = 72 – 25 = 47
d) 49 + (-51) = - (51 – 49) = -2
Toán lớp 6 trang 60 Vận dụng 3
a) Một thang máy đang ở tầng – 3, nó đi lên 5 tầng. Hỏi thang máy dừng lại ở tầng mấy?
b) Một thang máy đang ở tầng 3, nó đi xuống 5 tầng. Hỏi thang máy dừng lại ở tầng mấy?
(Ở một số tòa nhà, tầng mặt đất còn được gọi là tầng G).
Lời giải:
a) Ta có (-3) + 5 = 5 – 3 = 2.
Thang máy dừng ở tầng 2.
b) Ta có: 3 + (- 5) = - ( 5 – 3) = - 2.
Thang máy dừng ở tầng hầm -2.
Toán lớp 6 trang 60 Hoạt động khám phá 4
Tính và so sánh các cặp kết quả sau:
Lời giải:
+) Ta có: (-1) + (-3) = - (1 + 3) = -4;
(-3) + (-1) = - (3 + 1) = -4;
Suy ra (-1) + (-3) = (-3) + (-1) = -4.
Vậy (-1) + (-3) = (-3) + (-1) .
+) Ta có: (-7) + (+6) = - ( 7 – 6) = -1;
(+6) + (- 7) = - ( 7 – 6 ) = -1;
Suy ra (-7) + (+6) = (+6) + (- 7) = - 1.
Vậy (+6) + (- 7) = (-7) + (+6).
Toán lớp 6 trang 60 Hoạt động khám phá 5
Lời giải:
Ta có:
[(-3) + 4] + 2 = (4 – 3) + 2 = 1 + 2 = 3;
(-3) + (4 + 2) = (-3) + 6 = 6 – 3 = 3;
[(-3) + 2] + 4 = - (3 – 2) + 4 = (-1) + 4 = 4 – 1 = 3.
Suy ra [(-3) + 4] + 2 = (-3) + (4 + 2) = [(-3) + 2] + 4 = 3.
Vậy [(-3) + 4] + 2 = (-3) + (4 + 2) = [(-3) + 2] + 4.
Toán lớp 6 trang 61 Thực hành 3
b) (-2 020) + 2 021 + 21 + (-22).
Lời giải:
a) 23 + (-77) + (-23) + 77
= [23 + (-23)] + [(-77) + 77] (tính chất giao hoán và kết hợp)
= 0 + 0
= 0.
b) (-2020) + 2021 + 21 + (-22)
= [(-2020) + (-22)] + ( 2021 + 21) (tính chất giao hoán và kết hợp)
= (-2042) + 2042
= 0.
Toán lớp 6 trang 61 Hoạt động khám phá 6:
b) So sánh kết quả của hai phép tính sau:
Lời giải:
a) Mũi khoan đang ở độ cao: 5 – 10 = -5 (m) so với mực nước biển.
b) Ta có: 5 – 2 = 3 và 5 + (-2) = 5 – 2 = 3
Do đó: 5 – 2 = 5 + (-2)
Vậy 5 – 2 = 5 + (-2).
Toán lớp 6 trang 62 Thực hành 4
Lời giải:
a) 6 – 9 = 6 + ( -9) = -3;
b) 23 – (-12) = 23 + 12 = 35;
c) (-35) – (-60) = (-35) + 60 = 25;
d) (-47) – 53 = (-47) + (-53) = - 100;
e) (-43) – (-43) = (-43) + (43) = 0
Toán lớp 6 trang 62 Hoạt động khám phá 7
Tính rồi so sánh các cặp kết quả sau:
d) + ( -15 – 4) và ( - 15 - 4);
Lời giải:
a) – (4 + 7) = - 11;
(-4 – 7) = (-4) + (-7) = -11;
Vậy – (4 + 7) = ( -4 – 7).
b) – (12 – 25) = - [12 + (-25)] = - (-13) =13;
(-12 + 25) = 25 – 12 = 13;
Vậy – (12 – 25) = ( -12 + 25).
c) – (- 8 + 7) = - (-1) = 1;
(8 – 7) = 1;
Vậy – (-8 +7) = (8 – 7).
d) + ( -15 – 4) = (-15) + (-4) = -19;
( - 15 - 4) = (-15) + (-4) = -19;
Vậy + ( -15 – 4) = ( - 15 - 4).
e) + (23 – 12) = + 11 = 11;
(23 – 12) = 11;
Vậy + (23 – 12) = 23 -12.
Toán lớp 6 trang 63 Thực hành 5
Tính T = - 9 + (-2) – (-3) + (-8).
Lời giải:
T = - 9 + (-2) – (-3) + (-8)
= [-9 – (-3)] + [(-2) + (-8)]
= [ - 9 + 3] + (- 10)
= -6 + (-10)
= -16.
B. Bài tập
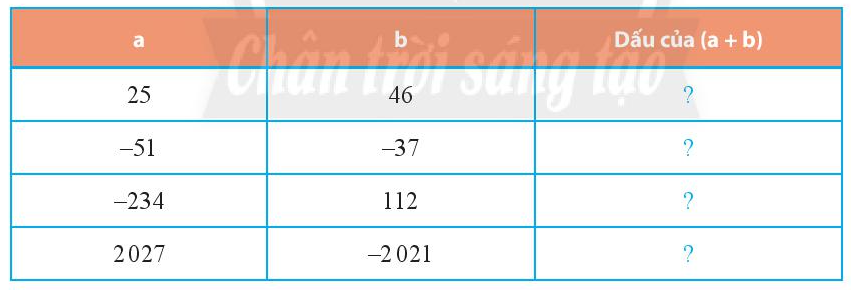
Không thực hiện phép tính, tìm dấu thích hợp cho dấu ? ở bảng sau:
Lời giải:
+) Với a = 25, b = 46 ta nhận thấy cả a và b đều là số nguyên dương nên dấu của (a + b) là dương.
+) Với a = - 51, b = -37 ta nhận thấy cả a và b đều là số nguyên âm nên dấu của (a + b) là âm.
+) Với a = - 234, b = 112 ta thấy a là số nguyên âm, b là số nguyên dương và 234 > 112 nên dấu của (a + b) là âm.
+) Với a = 2027, b = - 2021 ta thấy a là số nguyên dương, b là số nguyên âm và a > b nên dấu của (a + b) là dương.
Ta hoàn thành bảng sau:
|
a |
b |
Dấu (a + b) |
|
25 |
46 |
+ |
|
- 51 |
- 37 |
- |
|
- 234 |
112 |
- |
|
2027 |
- 2021 |
+ |
Lời giải:
a) 23 + 45 = 68
b) (-42) + (-54) = - (42 + 54) = - 96;
c) 2 025 + (-2 025) = 0;
d) 15 + (-14) = (15 – 14) = 1;
e) 35 + (-135) = - (135 – 35) = - 100.
Em hãy dùng số nguyên âm để giải bài toán sau:
Lời giải:
Tàu ngầm đang ở độ sâu 20 m hay tàu đang ở độ cao: - 20 m;
Tàu lặn thêm 15 m nữa được biểu diễn bởi: - 15m;
Khi đó tàu ngầm ở : (- 20) + (-15) = - 35 (m)
Do đó tàu ngầm ở độ cao - 35 m hay tàu ở độ sâu 35 m.
Vậy độ sâu của tàu ngầm ở độ sâu 35 m.
Lời giải:
Thang máy đang ở tầng 3 đi lên 7 tầng và sau đó đi xuống 12 tầng sẽ đến: 3 + 7 – 12 = 10 – 12 = -2.
Nghĩa là lúc này thang máy đang ở tầng hầm thứ hai.
Lời giải:
a) 6 – 8 = 6 + (-8) = -2;
b) 3 – (-9) = 3 + 9 = 12;
c) (-5) – 10 = - (10 + 5) = -15;
d) 0 – 7 = -7;
e) 4 – 0 = 4;
g) (-2) – (-10) = (-2) + 10 = 10 – 2 = 8.
b) S = (-2 021) - (199 – 2 021).
Lời giải:
a) S = (45 – 3 756) + 3 756 = 45 – 3 756 + 3 756 = 45 + [(– 3 756) + 3 756]
= 45 + 0 = 45
b) S = (-2 021) - (199 – 2 021) = (-2 021) + (-199) + 2 021
= [(-2 021) + 2 021] + (- 199) = 0 + (- 199) = - 199
a) (4 + 32 + 6) + (10 – 36 - 6);
b) (77 + 22 – 65) - (67 + 12 - 75);
c) - (-21 + 43 + 7) – (11 – 53 - 17).
Lời giải:
a) (4 + 32 + 6) + (10 – 36 - 6)
= 4 + 32 + 6 + 10 – 36 – 6
= 36 + 6 + 10 – 36 – 6
= (36 – 36) + ( 6 – 6) + 10
= 0 + 0 + 10
= 10.
b) (77 + 22 – 65) - (67 + 12 - 75)
= 77 + 22 – 65 – 67 – 12 + 75
= (77 – 67) + (22 – 12) + ( - 65 + 75)
= 10 + 10 + 10
= 30.
c) - (-21 + 43 + 7) – (11 – 53 - 17)
= 21 – 43 – 7 – 11 + 53 + 17
= (21 – 11) + ( -43 + 53) + (-7 + 17)
= 10 + 10 + 10
= 30.
Archimedes (Ác-si-mét) là nhà bác học người Hi Lạp, ông sinh năm 287 TCN và mất năm 212 TCN.
a) Em hãy dùng số nguyên âm để ghi năm sinh năm mất của Archimedes.
b) Em hãy cho biết Archimedes mất năm bao nhiêu tuổi?
Lời giải:
a)
Archimedes sinh năm 287 TCN hay năm sinh của Archimedes là năm - 287
Ông mất năm 212 TCN hay năm mất của Archimedes: - 212
b) Ta tính tuổi của Archimedes bằng cách lấy năm mất trừ đi năm sinh.
Tuổi của nhà bác học là: (-212) – (-287) = (-212) + 287 = 75 (tuổi)
Vậy Archimedes mất năm 75 tuổi.
Lý thuyết Toán 6 Bài 3: Phép cộng và phép trừ hai số nguyên - Chân trời sáng tạo
1. Cộng hai số nguyên cùng dấu
− Muốn cộng hai số nguyên dương, ta cộng chúng như cộng hai số tự nhiên.
− Muốn cộng hai số nguyên âm, ta cộng hai số đối của chúng rồi thêm dấu trừ đằng trước kết quả.
− Tổng của hai số nguyên cùng dấu luôn cùng dấu với hai số nguyên đó.
Chú ý:
Cho a, b là hai số nguyên dương, ta có:
(+a) + (+b) = a + b
(−a) + (− b) = − (a + b)
Ví dụ: Thực hiện các phép tính sau:
a) 8 + 12;
b) (−15) + (−9);
c) (−65) + (−35).
Hướng dẫn giải
a) 8 + 12 = 11;
b) (−15) + (−9) = − (15 + 9) = −24;
c) (−65) + (−35) = − (65 + 35) = −100.
2. Cộng hai số nguyên khác dấu
a) Cộng hai số đối nhau
Tổng hai số nguyên đối nhau luôn luôn bằng 0: a + (− a) = 0.
Ví dụ: 20 và −20 là hai số đối nhau.
Khi đó, 20 + (− 20) = 0.
b) Cộng hai số nguyên khác dấu không đối nhau
Muốn cộng hai số nguyên khác dấu không đối nhau, ta làm như sau:
− Nếu số dương lớn hơn số đối của số âm thì ta lấy số dương trừ đi số đối của số âm.
− Nếu số dương bé hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ trước kết quả.
Chú ý: Khi cộng hai số nguyên trái dấu:
− Nếu số dương lớn hơn số đối của số âm thì ta có tổng dương.
− Nếu số dương bằng số đối của số âm thì ta có tổng bằng 0.
− Nếu số dương bé hơn số đối của số âm thì ta có tổng âm.
Ví dụ: Thực hiện các phép tính sau:
a) 18 + (−21);
b) (−6) + 12;
c) 25 + (−14).
Hướng dẫn giải
a) 18 + (−21) = − (21 – 18) = − 3;
b) (−6) + 12 = 12 – 6 = 6;
c) 25 + (−14) = 25 – 14 = 11.
3. Tính chất của phép cộng các số nguyên
a) Tính chất giao hoán
Phép cộng các số nguyên có tính chất giao hoán, nghĩa là: a + b = b + a
Chú ý: a + 0 = 0 + a = a.
Ví dụ:
25 + 18 = 18 + 25;
16 + (−35) = (−35) + 16;
(−26) + (−47) = (−47) + (−26).
b) Tính chất kết hợp
Phép cộng các số nguyên có tính chất kết hợp: (a + b) + c = a + (b + c)
Chú ý:
− Tổng (a + b) + c hoặc a + (b + c) là tổng của ba số nguyên a, b, c và viết là a + b + c; với a, b, c là các số hạng của tổng.
− Để tính tổng của nhiều số, ta có thể thay đổi tùy ý thứ tự các số hạng (tính giao hoán), hoặc nhóm tùy ý các số hạng (tính kết hợp) để việc tính toán được đơn giản và thuận lợi hơn.
Ví dụ: Thực hiện các phép tính sau:
a) 25 + (−75) + (−25) + 75;
b) (−2 022) + 2 021 + 21 + (−20).
Hướng dẫn giải
a) 25 + (−75) + (−25) + 75
= 25 + (−25) + (−75) + 75 (tính chất giao hoán)
= [25 + (−25)] + [(−75) + 75] (tính chất kết hợp)
= 0 + 0 = 0.
b) (−2 022) + 2 021 + 21 + (−20)
= (−2 022) + (−20) + 2 021 + 21 (tính chất giao hoán)
= [(−2 022) + (−20)] + (2021 + 21) (tính chất kết hợp)
= (−2042) + 2042 = 0.
4. Phép trừ hai số nguyên
Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b.
a – b = a + (−b)
Chú ý:
− Cho hai số nguyên a và b. Ta gọi a – b là hiệu của a và b (a được gọi là số bị trừ, b là số trừ).
− Phép trừ luôn thực hiện được trong tập hợp số nguyên.
Như vậy, hiệu của hai số nguyên a và b là tổng của a và số đối của b.
Ví dụ: Thực hiện các phép tính sau:
a) 5 – 11;
b) 26 – (–12);
c) (–38) – (–50).
Hướng dẫn giải
a) 5 – 11 = 5 + ( −11) = −6;
b) 26 – (–12) = 26 + 12 = 38;
c) (–38) – (–50) = (−38) + 50 = 50 – 38 = 12.
5. Quy tắc dấu ngoặc
Khi bỏ dấu ngoặc, nếu đằng trước dấu ngoặc:
• có dấu “+”, thì vẫn giữ nguyên dấu của các số hạng trong ngoặc
+ (a + b – c) = a + b – c
• có dấu “–”, thì phải đổi dấu tất cả các số hạng trong ngoặc
− (a + b – c) = − a − b + c
Ví dụ: Tính M = (− 25) + (−2) – (−75) + (−8).
Hướng dẫn giải
M = (− 25) + (−2) − (−75) + (−8)
= [(− 25) − (−75)] + [(−2) + (−8)]
= − (25 + 75) + (− 10)
= (− 100) + (− 10)
= − (100 + 10) = −110.
Xem thêm lời giải bài tập Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Chân trời sáng tạo
- Soạn văn lớp 6 (ngắn nhất) - Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 6 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 6 - Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn 6 - Chân trời sáng tạo
- Văn mẫu lớp 6 – Chân trời sáng tạo
- Giải sgk Địa Lí 6 – Chân trời sáng tạo
- Giải sbt Địa Lí 6 – Chân trời sáng tạo
- Lý thuyết Địa Lí 6 – Chân trời sáng tạo
- Giải sgk Lịch sử 6 – Chân trời sáng tạo
- Giải sbt Lịch sử 6 – Chân trời sáng tạo
- Lý thuyết Lịch sử lớp 6 – Chân trời sáng tạo
- Giải sgk GDCD 6 – Chân trời sáng tạo
- Giải sbt GDCD 6 – Chân trời sáng tạo
- Lý thuyết GDCD 6 – Chân trời sáng tạo
- Giải sgk Công nghệ 6 – Chân trời sáng tạo
- Giải sbt Công nghệ 6 – Chân trời sáng tạo
- Lý thuyết Công nghệ 6 – Chân trời sáng tạo
- Giải sgk Khoa học tự nhiên 6 – Chân trời sáng tạo
- Giải sbt Khoa học tự nhiên 6 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 6 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 6 - Friends plus
- Trọn bộ Từ vựng Tiếng Anh 6 Friends plus đầy đủ nhất
- Ngữ pháp Tiếng Anh 6 Friends plus
- Giải sbt Tiếng Anh 6 - Friends plus
- Bài tập Tiếng Anh 6 Friends plus theo Unit có đáp án