Giải Toán 6 Bài tập cuối chương 2 - Chân trời sáng tạo

Toán lớp 6 trang 73 Câu 1

Chọn phát biểu đúng trong số các câu sau:

(A) Tập hợp số nguyên được kí hiệu là N.

(B) +2 không phải là một số tự nhiên.

(C) 4 không phải là một số nguyên.

(D) – 5 là một số nguyên.

Lời giải:

(A) Tập hợp số nguyên được kí hiệu là Z . Nên A sai.

(B) + 2 là một số tự nhiên nên B sai.

(C) 4 là một số nguyên nên C sai.

(D) – 5 là một số nguyên âm nên – 5 là một số nguyên nên D đúng.

Chọn D.

Toán lớp 6 trang 73 Câu 2

Trong các phát biểu sau đây, phát biểu nào sai?

(A) 3 > - 4.

(B) – 5 > - 9.

(C) – 1 < 0.

(D) – 9 > -8.

Lời giải:

Vì trên trục số điểm – 9 nằm bên trái -8 nên  -9 < -8. Do đó D sai.

Chọn D.

Toán lớp 6 trang 73 Câu 3

Kết quả của phép tính: 25 – (9 – 10) + (28 – 4) là:

(A) 50.

(B) 2.

(C) – 2.

(D) 48.

Lời giải:

25 – (9 – 10) + (28 – 4)

= 25 – (- 1) + 24

= 25 + 1 + 24

= 26 + 24

= 50.

Chọn A.

Toán lớp 6 trang 73 Câu 4

Kết quả của phép tính: (- 4) . (+21) . (- 25) . (- 2) là:

(A) 420.

(B) 4 200.

(C) – 4 200.

(D) - 420.

Lời giải:

(- 4) . (+21) . (- 25) . (- 2)

= [(-4) . (-25)] . [(+21) . (-2)] (tính chất giao hoán và kết hợp)

= 100 . (-42)

= - 4 200.

Chọn C.

B. Phần tự luận

Toán lớp 6 trang 73 Bài 1

Tính:

a) 73 – (2 – 9);

b) (- 45) – (27 – 8).

Lời giải:

a) 73 – (2 – 9) = 73 – (-7) = 73 + 7 = 80;

b) (- 45) – (27 – 8) = (-45) – 19 = (-45) + (-19) = -64.

Toán lớp 6 trang 73 Bài 2

Tìm hai số nguyên x, thỏa mãn:

a) $x^2=4$

b) $x^2=81$

Lời giải:

a) $x^2=4$

x² = 2² hoặc x² = (-2)²

x = 2 hoặc x = -2.

Vậy x = 2 hoặc x = -2.

b) x² = 81

x² = 9² hoặc x² = (-9)²

x = 9 hoặc x = - 9.

Vậy x = 9 hoặc x = - 9.

Toán lớp 6 trang 73 Bài 3

Tính các thương sau:

a) 12:6;

b) 24:(- 8);

c) (- 36):9;

d) (- 14):(- 7).

Lời giải:

a) 12:6 = 2;

b) 24:(- 8) = - (24 : 8) = -3;

c) (- 36):9 = - (36 : 9) = -4;

d) (- 14):(- 7) = 14 : 7 = 2.

Toán lớp 6 trang 73 Bài 4

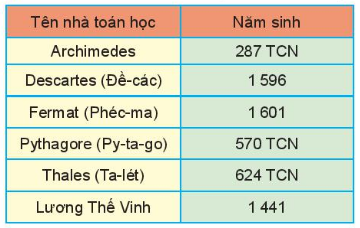
Cho biết năm sinh của một số nhà toán học.

Em hãy sắp xếp các số chỉ năm sinh của các nhà toán học theo thứ tự giảm dần.

Lời giải:

Archimedes có năm sinh 287 TCN nghĩa là năm thứ -287;

Pythagore có năm sinh 570 TCN nghĩa là năm thứ - 570;

Thales có năm sinh 624 TCN nghĩa là năm thứ - 624;

Ta có: 1 601 > 1 596 > 1 441 > - 287 > - 570 > - 624.

Số chỉ các năm sinh giảm dần:

1 601; 1 596; 1 441; - 287; - 570; - 624.

Toán lớp 6 trang 73 Bài 5

Một máy bay đang bay ở độ cao 5 000 m trên mực nước biển, tình cờ thẳng ngay bên dưới máy bay có một chiếc tàu ngầm đang lặn ở độ sâu 1 200 m dưới mực nước biển. Tính khoảng cách theo chiều thẳng đứng giữa máy bay và tàu ngầm.

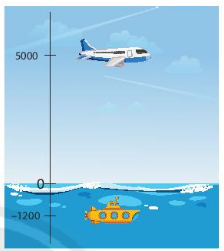
Lời giải:

Độ cao của tàu ngầm là: -1200 m.

Khoảng cách theo chiều thẳng đứng giữa máy bay và tàu ngầm là:

5 000 – (-1 200) = 5 000 + 1 200 = 6 200 (m)

Vậy khoảng cách theo chiều thẳng đứng giữa máy bay và tàu ngầm là 6 200 m.

Toán lớp 6 trang 73 Bài 6

Đố vui.

Tìm số nguyên thích hợp thay thế cho mỗi dấu ? trong bảng dưới đây sao cho tích của ba số ở ba ô liền nhau đều bằng 60.

Lời giải:

Theo quy luật, tích ở ba ô liên tiếp đều bằng 60, nghĩa là d.e.f = 60; e.f.g = 60

Suy ra: d.e.f= e.f.g$\Rightarrow$d = g.

Tương tự ta cũng sẽ có a.b.3 = 60 = b.3.c

Suy ra a = c.

Chứng minh hoàn toàn tương tự ta được: a = c = f = -4; b = d = g = i = x; 3 = e = h

Khi đó ta có dãy số:

-4

x

3

-4

x

3

-4

x

3

-4

x

Ta lại có: (-4).x.3 = 60

Suy ra x= -5

Vậy điền dãy số hoàn chỉnh như sau:

Toán lớp 6 trang 73 Bài 7

Hình vẽ dưới đây biểu diễn một người đi từ O đến A rồi quay về B. Đặt một bài toán phù hợp với hình vẽ.

Lời giải:

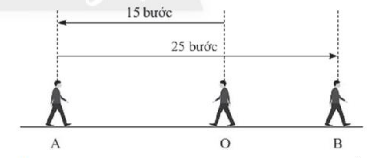
Bài toán: Một người đang đứng yên ở điểm O, người đó bước đi về điểm A bên trái 15  bước, rồi đi ngược lại về điểm B bên phải 25 bước (biết rằng các bước chân của người đó là như nhau).

a) Hỏi người đó đi từ O đến B hết bao nhiêu bước

b) So sánh số trên với tổng của hai số nguyên (- 15) + 25.

Lời giải bài toán

a) Người đó đi từ O đến B hết số bước chân là: 25 -15 = 10 ( bước).

b) Ta có: (-15) + 25 = 25 – 15 = 10.