Giải Toán 6 Bài 2: Hình chữ nhật – Hình thoi – Hình bình hành – Hình thang cân - Chân trời sáng tạo
Lời giải bài tập Toán lớp 6 Bài 2: Hình chữ nhật – Hình thoi – Hình bình hành – Hình thang cân sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6.
Giải Toán 6 Bài 2: Hình chữ nhật – Hình thoi – Hình bình hành – Hình thang cân
A. Các câu hỏi trong bài
Toán lớp 6 trang 80 Hoạt động khởi động
Quan sát hình dạng của bức tranh, cái diều, tấm bìa, mái nhà rông, em có biết đó là các hình gì?
Lời giải:
Hình dạng của bức tranh là hình chữ nhật.
Hình dạng của cái diều là hình thoi.
Hình dạng của tấm bìa là hình bình hành.
Hình dạng của mái nhà rông là hình thang cân.
Toán lớp 6 trang 80 Hoạt động khám phá 1
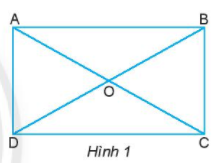
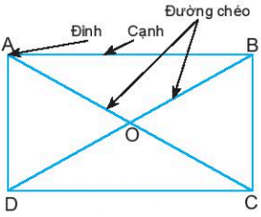
Cho hình chữ nhật ABCD (Hình 1).
a) Đo rồi so sánh các cạnh và góc của hình chữ nhật.
b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không.
c) AC và BD được gọi là hai đường chéo của hình chữ nhật. Hãy đo rồi so sánh AC và BD.
a) Sau khi tiến hành đo các cạnh và góc của hình chữ nhật ta có nhận xét sau:
- Độ dài cạnh AB bằng độ dài cạnh CD bằng 4,5 cm, độ dài cạnh AD bằng độ dài cạnh BC bằng 2,5 cm.
- Tất cả các góc của hình chữ nhật bằng nhau và bằng góc vuông.
b) Dùng eke để kiểm tra ta thấy cặp cạnh AB và CD song song với nhau, BC và AD song song với nhau.
c) Thực hiện đo độ dài của hai đường chéo AC và BD ta thấy độ dài cạnh AC bằng độ dài cạnh BD bằng 5,1cm.
Toán lớp 6 trang 81 Thực hành 1
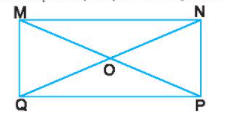
Đo và so sánh độ dài các đoạn OM, ON, OP và OQ của hình chữ nhật MNPQ.
Lời giải:
Tiến hành đo độ dài các đoạn OM, ON, OP và OQ ta thấy độ dài các đoạn bằng nhau và bằng 2,3 cm.
Toán lớp 6 trang 81 Vận dụng 1
Lời giải:
Ta ghép các hình a, b, c như sau:

Ta được bức tranh như hình d.
Toán lớp 6 trang 81 Thực hành 2
Vẽ hình chữ nhật ABCD có AB = 4 cm, AD = 3 cm theo hướng dẫn sau:
- Vẽ đoạn thẳng AB = 4 cm và đoạn thẳng AD = 3 cm vuông góc với nhau.
- Qua B vẽ đường thẳng vuông góc với AB.
- Qua D vẽ đường thẳng vuông góc với AD.
Hai đường thẳng này cắt nhau ở C.
Lời giải:
- Vẽ đoạn thẳng AB = 4 cm và đoạn thẳng AD = 3cm vuông góc với nhau.
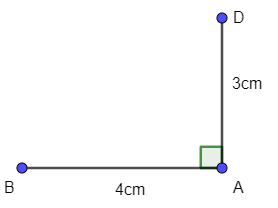
- Qua B vẽ đường thẳng vuông góc với AB.
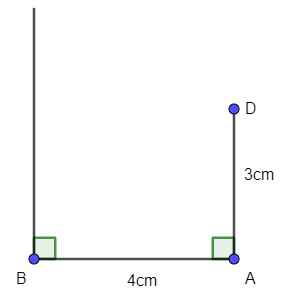
- Qua D vẽ đường thẳng vuông góc với AD.
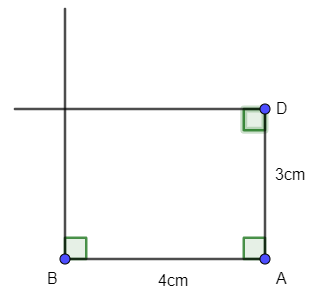
Hai đường thẳng này cắt nhau ở C.
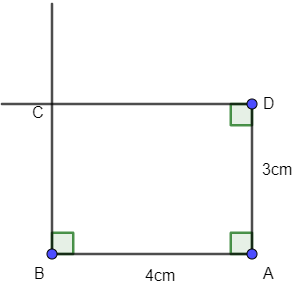
Ta được hình chữ nhật ABCD.
Toán lớp 6 trang 81 Vận dụng 2
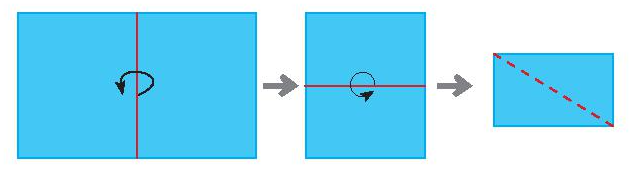
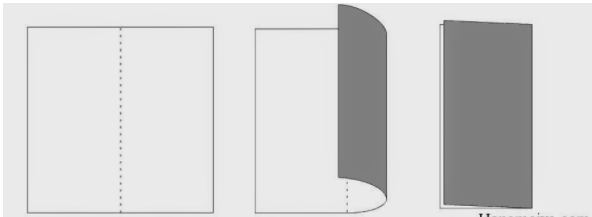
Hãy xếp và cắt một tờ giấy hình chữ nhật thành bốn hình chữ nhật có cùng chiều dài và chiều rộng.
Lời giải:
Chuẩn bị 1 tờ giấy A4 (giấy A4 có dạng hình chữ nhật)
- Gấp đôi tờ giấy A4 lại;
- Tiếp tục gập đôi nửa tờ giấy A4 đó.
- Sau đó dùng kéo cắt theo các nếp gấp ta được 4 hình chữ nhật có cùng chiều dài và chiều rộng.
Toán lớp 6 trang 81 Hoạt động khám phá 2
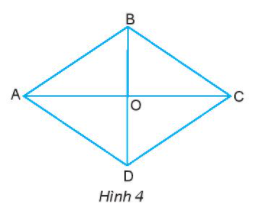
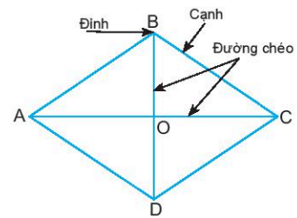
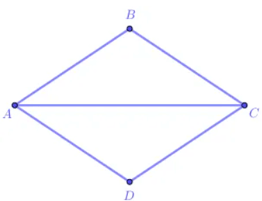
Cho hình thoi ABCD như hình 4.
a) Hãy so sánh các cạnh của hình thoi.
b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không.
Lời giải:
a) Sau khi thực hiện đo độ dài các cạnh của hình thoi ta rút ra được kết luận là các cạnh của hình thoi có độ dài bằng nhau: AB = BC = CD = DA.
b) Sử dụng eke để kiểm tra ta thấy hai cặp cạnh AB và CD, BC và AD song song với nhau.
c) Sử dụng eke kiểm tra hai đường chéo AC và BD ta thấy chúng vuông góc với nhau.
Toán lớp 6 trang 82 Thực hành 2
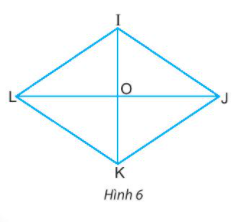
Cho hình thoi IJKL, hai đường chéo cắt nhau tại O (Hình 6).
- Dùng eke để kiểm tra xem hai đường chéo có vuông góc với nhau hay không.
- Dùng compa để kiểm tra hai đường chéo có cắt nhau tại trung điểm của mỗi đường hay không.
Lời giải:
- Hai đường chéo LJ, IK vuông góc với nhau.
- Dùng thước đo ta thấy, IO = OK, LO = OJ.
Do đó hai đường chéo LJ, IK cắt nhau tại trung điểm O của mỗi đường.
Toán lớp 6 trang 82 Thực hành 3
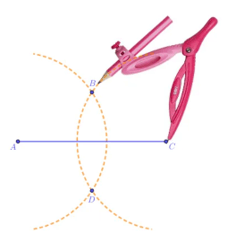
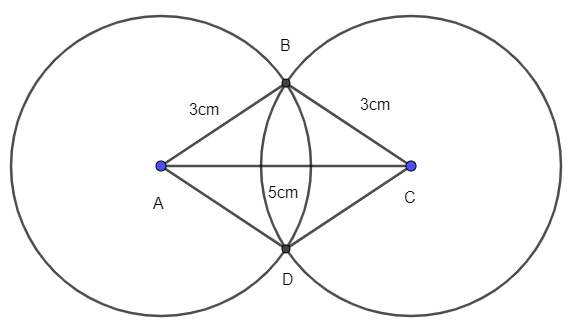
Vẽ hình thoi ABCD khi biết AB = 3 cm và đường chéo AC = 5 cm theo hướng dẫn sau:
- Nối B với A, B với C, D với A, D với C.
Lời giải
- Vẽ đoạn thẳng AC = 5cm.
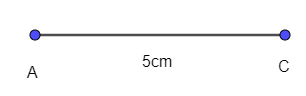
- Lấy A và C làm tâm, vẽ hai đường tròn bán kính 3 cm (hình vẽ), hai đường tròn này cắt nhau tại điểm B và D.
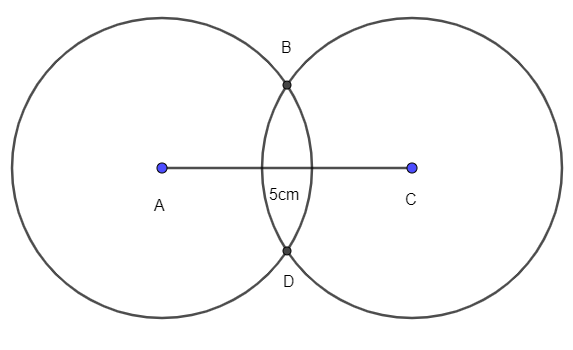
- Nối B với A, B với C, D với A, D với C. ABCD là hình thoi cần vẽ.
Toán lớp 6 trang 82 Vận dụng 3
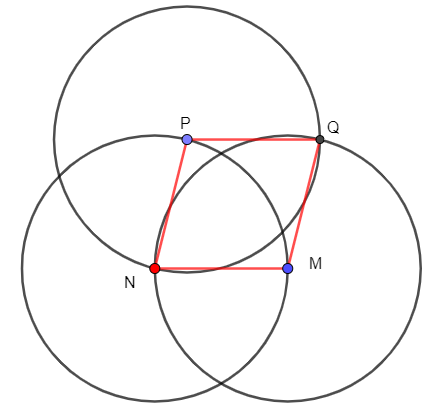
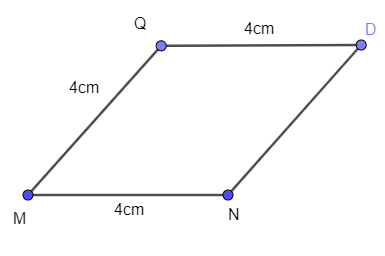
Vẽ hình thoi MNPQ biết cạnh MN = 4 cm. Em hãy thảo luận với các bạn về các hình vừa vẽ.
Lời giải:
Cách 1. Dùng thước và compa
- Vẽ cạnh MN = 4 cm.
- Vẽ đường tròn tâm N bán kính 4 cm
- Trên đường tròn này lấy điểm P, vẽ đường tròn tâm P bán kính 4 cm.
- Vẽ đường tròn tâm M bán kính 4 cm cắt đường tròn tâm P bán kính 4 cm tại Q.
- Nối N với P, P với Q, Q với M lại ta được hình thoi MNPQ.
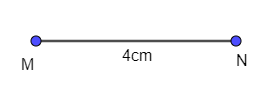
Cách 2. Dùng thước và eke
- Vẽ đoạn thẳng MN = 4 cm
- Vẽ đoạn thẳng MQ = 4 cm
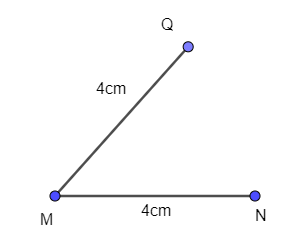
- Từ Q vẽ đường thẳng song song với MN, trên đường thẳng đó lấy điểm P sao cho PQ = 4 cm.
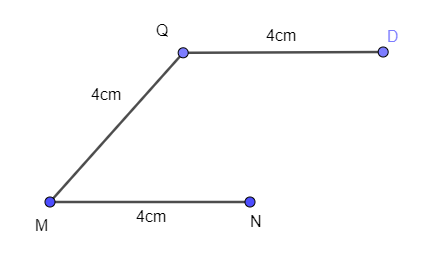
- Nối P với N ta được hình thoi MNPQ.
Toán lớp 6 trang 83 Hoạt động khám phá 3
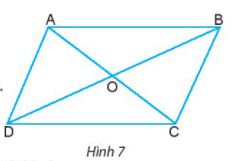
Cho hình bình hành ABCD như Hình 7.
a) Hãy đo rồi so sánh cạnh AB và CD; cạnh BC và AD.
b) Hãy kiểm tra xem các cặp cạnh AB và CD, BC và AD có song song với nhau không.
c) AC và BD được gọi là hai đường chéo của hình bình hành.
Hai đường chéo AC và BD cắt nhau tại O. Hãy so sánh OA và OC; OB và OD.
Lời giải:
a) Sau khi đo, ta thấy độ dài cạnh AB bằng độ dài CD, độ dài cạnh BC bằng độ dài cạnh AD.
b) Dùng eke để kiểm tra, ta có nhận xét các cặp cạnh AB và CD, BC và AD song song với nhau.
c) Sau khi đo độ dài OA và OC; OB và OD ta thấy độ dài OA bằng độ dài OC, độ dài OB bằng độ dài OD.
Toán lớp 6 trang 83 Thực hành 4
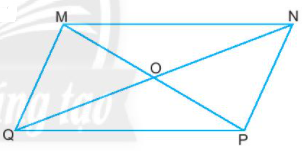
Quan sát hình bình hành bên và cho biết
- Góc đỉnh M của hình bình hành MNPQ bằng góc nào?
- OM, ON lần lượt bằng những đoạn nào?
Lời giải:
- Góc đỉnh M của hình bình hành MNPQ bằng góc tại đỉnh P.
- Ta có OM = OP, ON = OQ.
Toán lớp 6 trang 83, 84 Thực hành 5
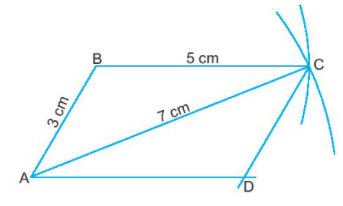
Vẽ hình bình hành ABCD khi biết AB = 3 cm, BC = 5 cm và đường chéo AC = 7 cm theo hướng dẫn sau:
ABCD là hình bình hành cần vẽ.
- Dùng compa để kiểm tra xem các cạnh đối diện có bằng nhau hay không.
Lời giải:
Thực hiện theo hướng dẫn trên, ta vẽ được hình bình hành ABCD.
- Vẽ đoạn thẳng AB = 3 cm.
- Vẽ đường tròn tâm A bán kính 7 cm; vẽ đường tròn tâm B bán kính 5 cm; hai đường tròn cắt nhau tại C. Nối B với C.
- Từ A kẻ hai đường thẳng song song với BC; từ C kẻ đường thẳng song song với AB; hai đường thẳng này cắt nhau tại D.
ABCD là hình bình hành cần vẽ.
Sử dụng compa để kiểm tra các cặp cạnh đối diện của hình vẽ như sau:
- Ta đặt một đầu của compa vào điểm A, mở compa để đầu còn lại trùng với B.
- Tiếp theo, giữ nguyên đoạn compa đó, đặt một đầu vào điểm C đầu còn lại ta thấy đi qua điểm D. Như vậy độ dài đoạn AB = CD.
- Thực hiện tương tự với cặp cạnh AD và BC ta thu được AD = BC.
Hình bình hành có các cặp cạnh AD = BC, AB = DC.
Toán lớp 6 trang 84 Vận dụng 5
Lời giải:
- Vẽ đoạn thẳng AC = 5 cm.
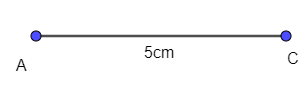
- Lấy trung điểm O của đoạn thẳng AC. Vẽ đường tròn tâm O bán kính 3,5 cm.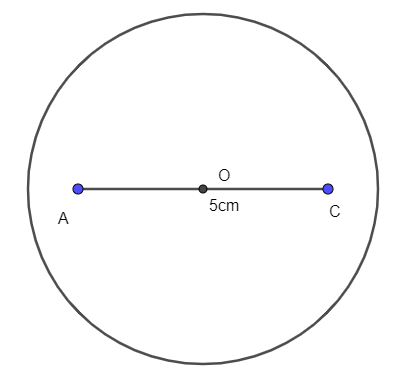
- Vẽ đường thẳng đi qua tâm O cắt đường tròn tại hai điểm B và D.
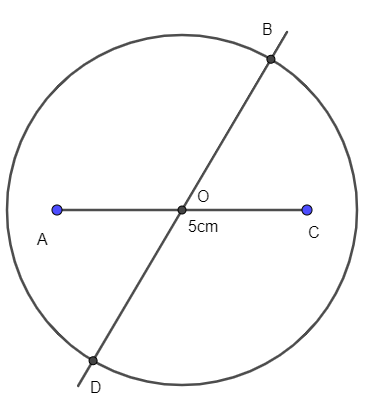
- Nối A với B, B với C, C với D, D với A, ta được hình bình hành ABCD.
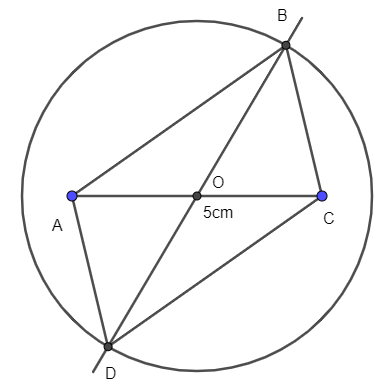
Toán lớp 6 trang 84 Hoạt động khám phá 4
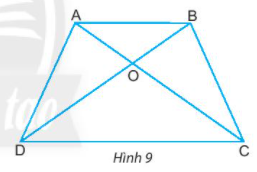
Cho hình thang cân như Hình 9.
a) Hãy đo rồi so sánh hai cạnh bên BC và AD.
b) Hãy kiểm tra xem AB có song song với CD hay không.
c) AC và BD được gọi là hai đường chéo. Hãy đo rồi so sánh AC và BD.
Lời giải:
a) Sau khi đo độ dài hai cạnh bên, ta có kết quả sau BC = AD = 3,05 cm.
Vậy độ dài cạnh bên BC bằng độ dài AD.
b) Dùng eke kiểm tra ta thấy AB song song với CD.
c) Sau khi đo, ta được: AC = BD = 4,8 cm.
Do đó AC = BD.
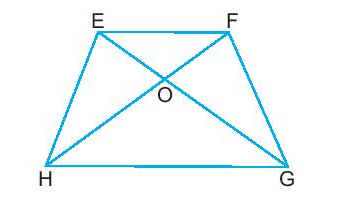
Toán lớp 6 trang 85 Thực hành 6
Cho hình thang cân như hình bên.
- Góc ở đỉnh H của hình thang cân EFGH là bằng góc nào?
- EG, EH lần lượt bằng các đoạn thẳng nào?
Lời giải:
- Tiến hành đo góc, ta nhận thấy góc H bằng góc G.
- Tiến hành đo các cạnh, ta có: EG = FH, EH = FG.
Trong các hình sau đây hình nào là hình chữ nhật, hình bình hành, hình thoi, hình thang cân?
Lời giải:
Hình a: Hình thoi;
Hình b: Hình thang cân;
Hình c: Hình chữ nhật;
Hình d: Hình bình hành.
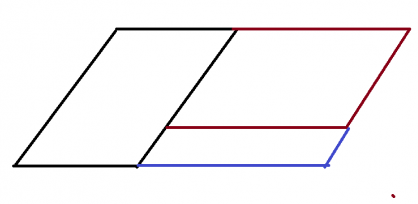
Đo rồi cho biết độ dài các cạnh của mỗi hình chữ nhật sau:
Lời giải:
+) Với hình chữ nhật màu xanh, ta đo thấy hai kích thước của hình là: 4 cm và 2 cm.
+) Với hình chữ nhật màu vàng, ta đo thấy hai kích thước của hình là: 5 cm và 3 cm.
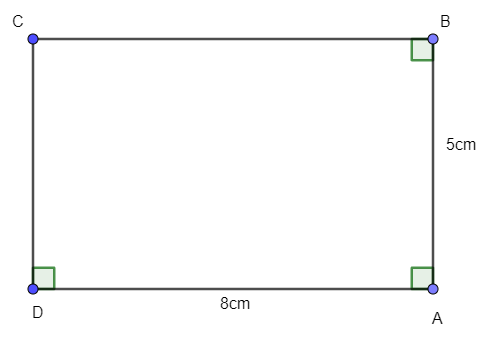
Vẽ hình chữ nhật ABCD, biết AB = 5 cm, AD = 8 cm.
Lời giải:
- Vẽ hai đoạn thẳng AB = 5 cm, AD = 8 cm vuông góc với nhau.
- Dựng đường thẳng qua B vuông góc với AB.
- Dựng đường thẳng qua D vuông góc với AD.
- Hai đường thẳng trên cắt nhau tại C. Ta được hình chữ nhật ABCD.
Lời giải:
Từ 4 tam giác đều như hình vẽ bên dưới:
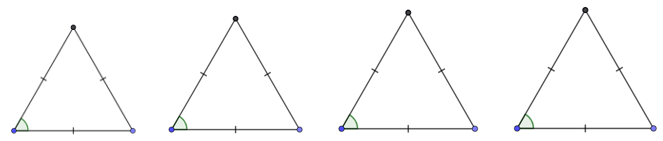
Ta ghép lại được hình bình hành như hình vẽ bên dưới:
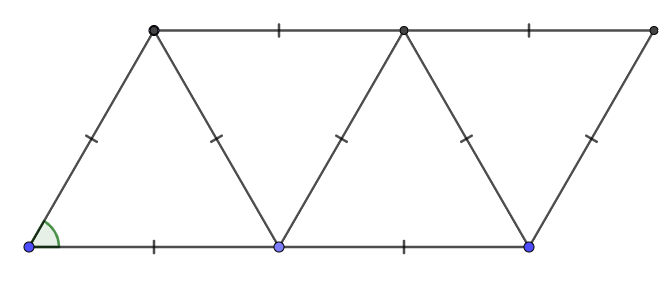
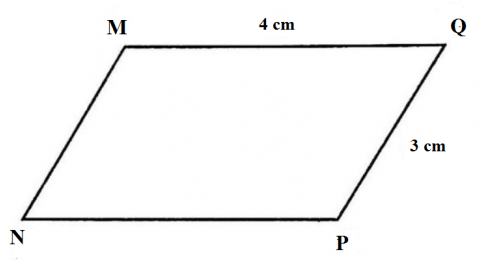
Vẽ hình bình hành MNPQ, biết: MN = 3 cm, NP = 4 cm.
Lời giải:
- Vẽ hai đoạn thẳng MN và NP như hình dưới sao cho MN = 3 cm, NP = 4 cm.
- Vẽ đường thẳng qua P song song với MN.
- Trên đường thẳng lấy điểm Q sao cho PQ = 3cm.
- Nối Q với M ta được hình bình hành MNPQ.
Lời giải:
Hình vừa cắt được là hình thoi (hình màu trắng)
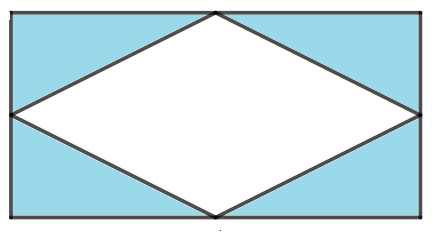
Hai đường chéo của hình vừa cắt được vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
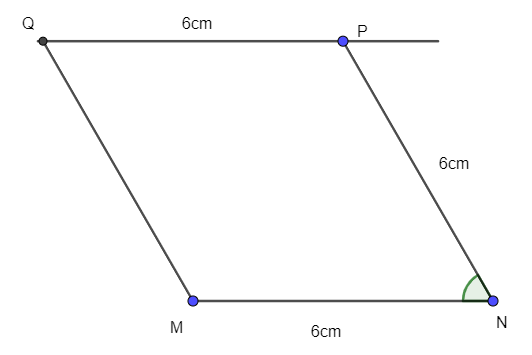
Vẽ hình thoi MNPQ biết góc MNP bằng 60° và MN = 6 cm.
Lời giải:
- Vẽ đoạn thẳng MN = 6cm.
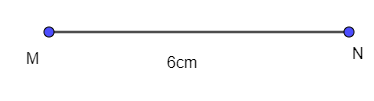
- Vẽ góc MNP bằng 60° và NP = 6cm.
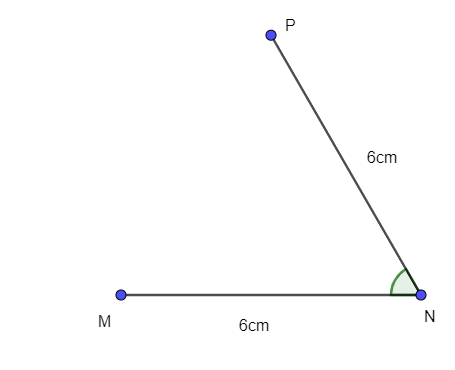
- Vẽ đường thẳng qua P song song với MN.
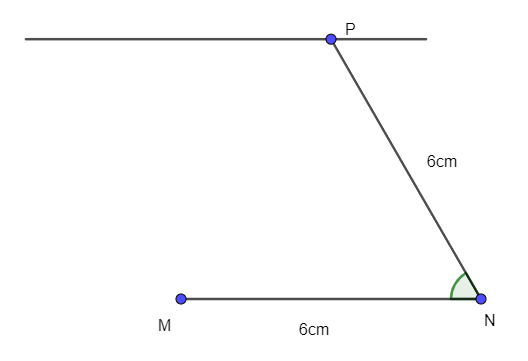
- Trên đường thẳng này lấy điểm Q sao cho PQ = 6cm.
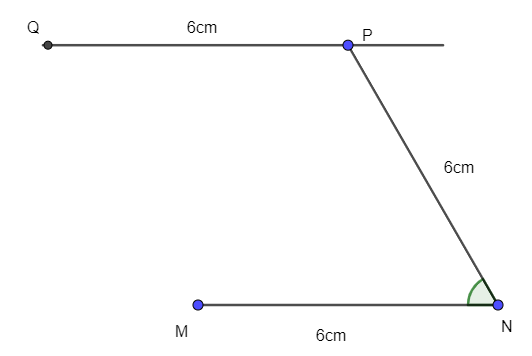
- Nối Q với M ta được thoi MNPQ.
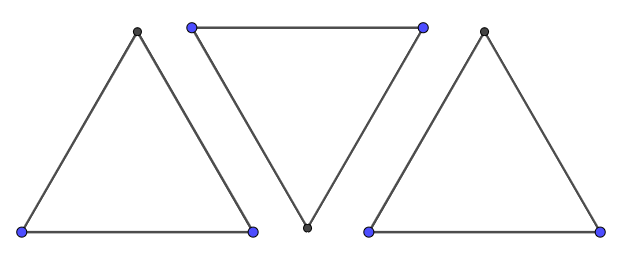
Cắt ba hình tam giác đều cạnh 4 cm rồi ghép lại thành một hình thang cân.
Lời giải:
Ta có ba tam giác đều như sau:
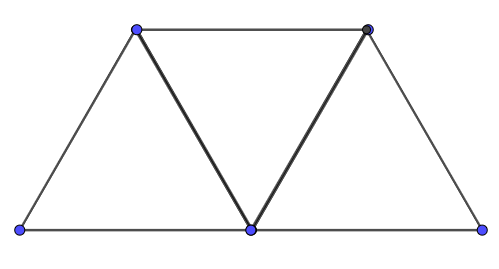
Sau đó ghép lại ta được hình thang cân bên dưới:
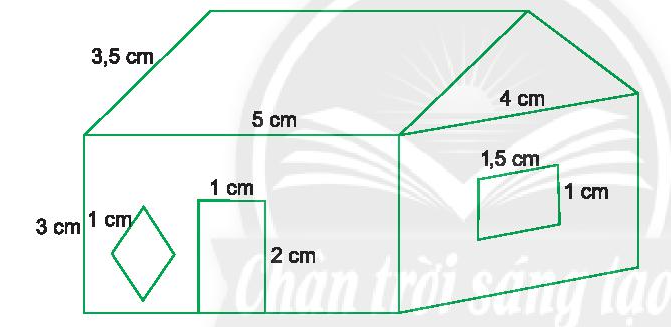
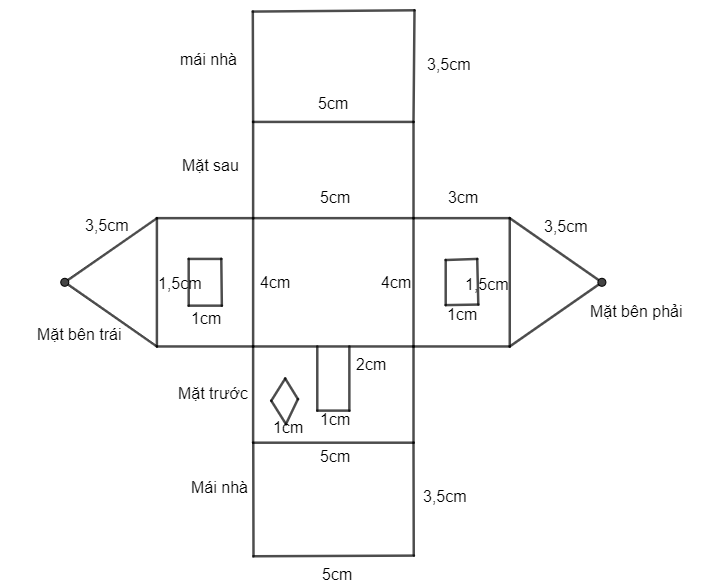
Vẽ sơ đồ ngôi nhà theo kích thước các cạnh nêu ra trong hình vẽ dưới đây.
Lời giải:
Ta vẽ được sơ đồ sau:
Lý thuyết Toán 6 Bài 2: Hình chữ nhật, Hình thoi, Hình bình hành, Hình thang cân - Chân trời sáng tạo
1. Hình chữ nhật
Hình chữ nhật có:
+ Bốn đỉnh.
+ Hai cặp cạnh đối diện bằng nhau.
+ Hai cặp cạnh đối diện song song.
+ Bốn góc ở các đỉnh bằng nhau và bằng góc vuông.
+ Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Ví dụ:
Hình chữ nhật ABCD có:
- Bốn đỉnh A, B, C, D.
- Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường:
AC = BD và OA = OC; OB = OD.
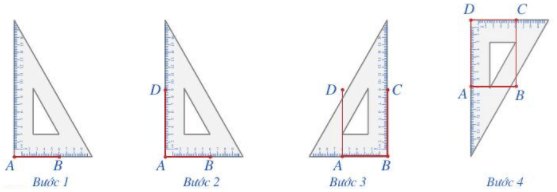
Cách vẽ hình chữ nhật
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 6 cm.
Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 9 cm.
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 9 cm.
Bước 4. Vẽ đoạn thẳng CD. Ta được hình chữ nhật ABCD.
2. Hình thoi
Hình thoi có:
+ Bốn đỉnh.
+ Bốn cạnh bằng nhau.
+ Hai cặp cạnh đối diện song song với nhau.
+ Hai đường chéo vuông góc với nhau.
Ví dụ:
Hình thoi ABCD có:
- Bốn đỉnh A, B, C, D.
- Bốn cạnh bằng nhau: AB = BC = CD = DA;
- Hai cạnh đối AB và CD, AD và BC song song với nhau.
- Hai đường chéo AC và BD vuông góc với nhau.
Cách vẽ hình thoi
Ví dụ: Dùng thước và compa vẽ hình thoi ABCD, biết AB = 5 cm và AC = 8 cm.
Hướng dẫn giải
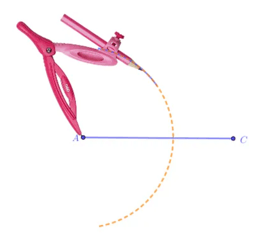
Bước 1. Dùng thước vẽ đoạn thẳng AC = 8 cm.
Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính 5 cm.
Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính 5cm; phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.
Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA. Ta được hình thoi ABCD (như hình vẽ).
3. Hình bình hành
Hình bình hành có:
+ Bốn đỉnh.
+ Hai cặp cạnh đối diện bằng nhau.
+ Hai cặp cạnh đối diện song song.
+ Hai cặp góc đối diện bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
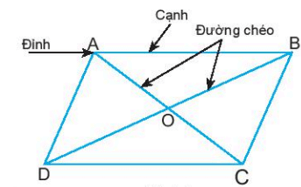
Ví dụ:
Hình bình hành ABCD có:
- Bốn đỉnh A, B, C, D.
- Hai cặp cạnh đối diện bằng nhau: AB = CD; BC = AD.
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Hai cặp góc đối diện bằng nhau: góc đỉnh A bằng góc đỉnh C; góc đỉnh B bằng góc đỉnh D.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: OA = OC; OB = OD.
Cách vẽ hình bình hành
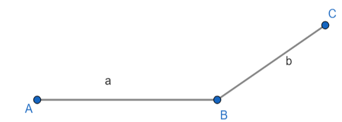
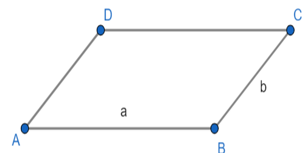
Hình bình hành ABCD có hai cạnh là a và b.
Bước 1: Vẽ đoạn thẳng AB = a (cm).
Bước 2: Vẽ đường thẳng đi qua B. Lấy điểm C trên đường thẳng đó sao cho BC = b (cm).
Bước 3: Vẽ đường thẳng đi qua A và song song với cạnh BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.
4. Hình thang cân
Hình thang cân có:
+ Hai cạnh đáy song song.
+ Hai cạnh bên bằng nhau.
+ Hai góc kề một đáy bằng nhau.
+ Hai đường chéo bằng nhau.
Ví dụ:
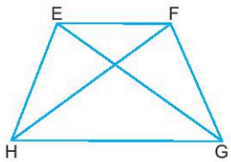
Hình thang cân EFGH có:
- Hai cạnh đáy song song: EF song song với GH.
- Hai cạnh bên bằng nhau: EH = FG.
- Hai góc kề một đáy bằng nhau: góc đỉnh E bằng góc đỉnh F, góc đỉnh G bằng góc đỉnh H.
- Hai đường chéo bằng nhau: EG = FH.
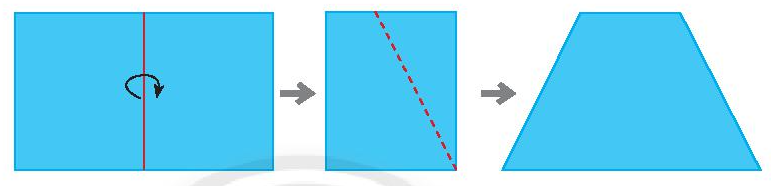
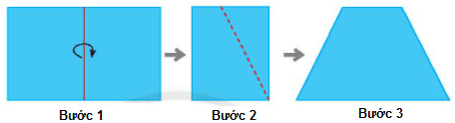
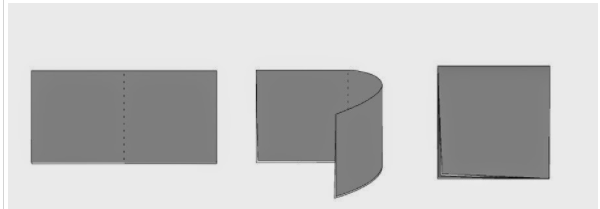
Cách gấp hình thang cân
Bước 1: Gấp đôi một tờ giấy hình chữ nhật.
Bước 2: Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh đối diện (cạnh không chứa nếp gấp). Cắt theo đường nét đứt như hình minh họa.
Bước 3: Mở tờ giấy ra ta được một hình thang cân.
Xem thêm lời giải bài tập Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Chân trời sáng tạo
- Soạn văn lớp 6 (ngắn nhất) - Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 6 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 6 - Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn 6 - Chân trời sáng tạo
- Văn mẫu lớp 6 – Chân trời sáng tạo
- Giải sgk Địa Lí 6 – Chân trời sáng tạo
- Giải sbt Địa Lí 6 – Chân trời sáng tạo
- Lý thuyết Địa Lí 6 – Chân trời sáng tạo
- Giải sgk Lịch sử 6 – Chân trời sáng tạo
- Giải sbt Lịch sử 6 – Chân trời sáng tạo
- Lý thuyết Lịch sử lớp 6 – Chân trời sáng tạo
- Giải sgk GDCD 6 – Chân trời sáng tạo
- Giải sbt GDCD 6 – Chân trời sáng tạo
- Lý thuyết GDCD 6 – Chân trời sáng tạo
- Giải sgk Công nghệ 6 – Chân trời sáng tạo
- Giải sbt Công nghệ 6 – Chân trời sáng tạo
- Lý thuyết Công nghệ 6 – Chân trời sáng tạo
- Giải sgk Khoa học tự nhiên 6 – Chân trời sáng tạo
- Giải sbt Khoa học tự nhiên 6 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 6 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 6 - Friends plus
- Trọn bộ Từ vựng Tiếng Anh 6 Friends plus đầy đủ nhất
- Ngữ pháp Tiếng Anh 6 Friends plus
- Giải sbt Tiếng Anh 6 - Friends plus
- Bài tập Tiếng Anh 6 Friends plus theo Unit có đáp án