Giải Toán 6 Bài 7: Số đo góc. Các góc đặc biệt - Chân trời sáng tạo

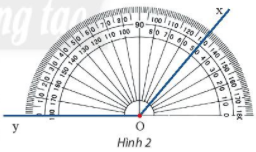
Toán lớp 6 trang 89 Câu hỏi khám phá 1: Dùng thước đo góc, xác định số đo của góc xOy cho trước.

- Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

- Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Oy) đi qua vạch 0 của thước và thước chồng lên phần trong của góc như Hình 2.

- Bước 3: Xác định xem cạnh còn lại của góc (cạnh Ox) đi qua vạch chỉ số nào trên thước đo góc, ta sẽ được số đo của góc đó.

Lời giải:

Học sinh thực hành theo trình tự các bước như trên.

Nhận thấy tia Ox đi qua vạch chỉ số 130 của thước đo góc.

Vậy số đo góc xOy là 130^o.

Toán lớp 6 trang 89 Câu hỏi thực hành 1: Cho góc xOy như hình vẽ. Em hãy dùng thước đo góc đo góc xOy.

Lời giải:

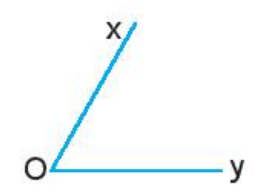
Dùng thước đo góc, xác định số đo của góc xOy như sau:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Oy) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh Ox đi qua vạch chỉ số 60 của thước đo góc.

Vậy $\widehat{xOy}$ = 60^o.

Giải Toán 6 trang 90 Tập 2

Toán lớp 6 trang 90 Câu hỏi thực hành 2

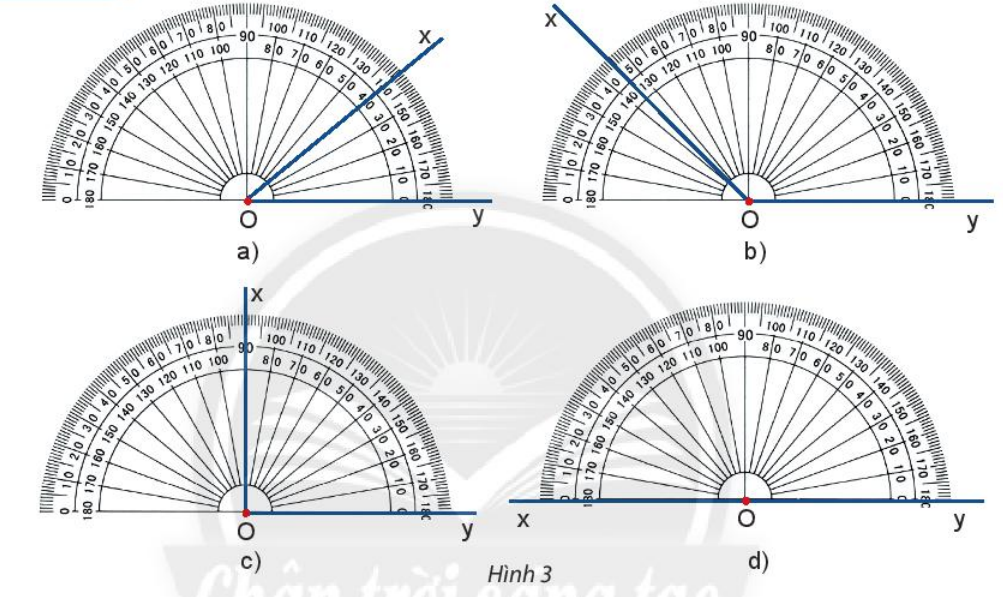
– Mỗi góc trong Hình 3 có số đo là bao nhiêu?

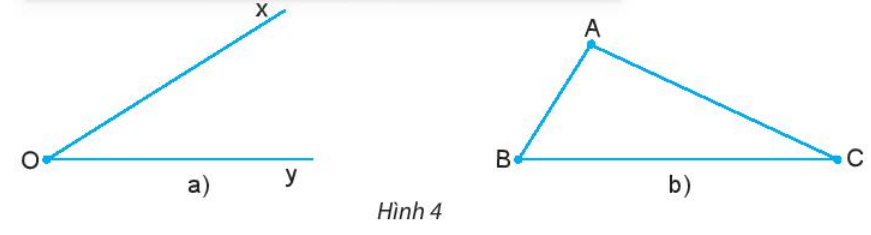
- Dùng thước đo góc để xác định số đo các góc trong Hình 4.

Lời giải:

* Trong Hình 3 có:

- Đỉnh O trong mỗi góc trong hình trên đều trùng với tâm của thước.

- Một cạnh của góc là cạnh Oy đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

- Cần xác định xem cạnh còn lại của góc (cạnh Ox) đi qua vạch chỉ số nào trên thước đo góc, ta sẽ được số đo của góc đó.

Số đo của mỗi góc trong Hình 3:

- Trong hình a) cạnh Ox đi qua vạch chỉ số 40 của thước đo góc.

Do đó số đo góc xOy là 40^o.

- Trong hình b) cạnh Ox đi qua vạch chỉ số 135 của thước đo góc.

Do đó số đo góc xOy là 135^o.

- Trong hình c) cạnh Ox đi qua vạch chỉ số 90 của thước đo góc.

Do đó số đo góc xOy là 90^o.     

- Trong hình d) cạnh Ox đi qua vạch chỉ số 180 của thước đo góc.

Do đó số đo góc xOy là 180^o. 

Vậy số đo mỗi góc trong Hình 3 là: 

Hình a) $\widehat{xOy}$ = 40^o; 

Hình b) $\widehat{xOy}$ = 135^o;

Hình c) $\widehat{xOy}$ = 90^o;

Hình d) $\widehat{xOy}$ = 180^o.

* Trong Hình 4 có:

- Hình a) có một góc là $\widehat{xOy}$.

- Hình b) có ba góc là: $\widehat{BAC}$, $\widehat{ABC}$, $ACB$.

Dùng thước đo góc, xác định số đo của mỗi góc trong Hình 4 như sau:

• Đo góc xOy:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Oy) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh Ox. Ta thấy cạnh Ox đi qua vạch chỉ số 95 trên thước đo góc.

Do đó, $\widehat{xOy}$ = 95^o.

• Đo góc BAC:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh A của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh AB) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh AC. Ta thấy cạnh AC đi qua vạch chỉ số 58 trên thước đo góc.

Do đó, $\widehat{BAC}$ = 58^o.

• Đo góc ABC:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh B của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh BC) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh BA. Ta thấy cạnh BA đi qua vạch chỉ số 58 trên thước đo góc.

Do đó, $\widehat{ABC}$ = 58^o. 

• Đo góc ACB:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh C của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh CB) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh CA. Ta thấy cạnh CA đi qua vạch chỉ số 27 trên thước đo góc.

Do đó, $\widehat{ACB}$ = 27^o.

Vậy số đo mỗi góc trong Hình 4 là: 

Hình a) $\widehat{xOy}$ = 32^o; 

Hình b) $\widehat{BAC}$ = 58^o; $\widehat{ABC}$ = 58^o; $\widehat{ACB}$ =  27^o.

Giải Toán 6 trang 91 Tập 2

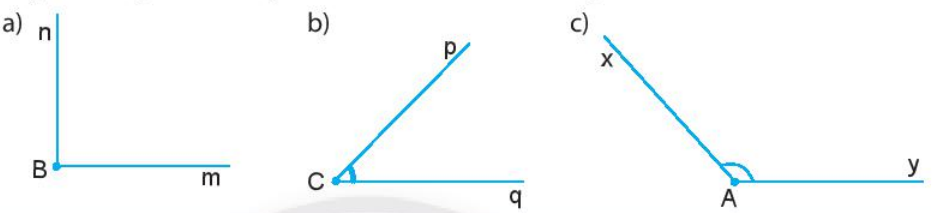
Toán lớp 6 trang 91 Câu hỏi khám phá 2: Hãy đo các góc dưới đây và so sánh số đo của chúng với 90°.

Lời giải:

Đo các góc trong hình trên và so sánh số đo của góc đó với 90° như sau:

a) Đo góc mBn:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh B của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Bm) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh Bn. Ta thấy cạnh Bn đi qua vạch chỉ số 90 trên thước đo góc.

Vậy $\widehat{mBn}$ = 90^o. 

b) Đo góc pCq:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh C của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Cp) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh Cq. Ta thấy cạnh Cq đi qua vạch chỉ số 45 trên thước đo góc.

Do đó, $\widehat{pCq}$ = 45^o.

Vì 45^o < 90^o nên $\widehat{pCq}$ < 90^o.

Vậy $\widehat{pCq}$ = 45^o và $\widehat{pCq}$ < 90^o.

c) Đo góc xOy:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Oy) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh Ox. Ta thấy cạnh Ox đi qua vạch chỉ số 130 trên thước đo góc.

Do đó, $\widehat{xOy}$= 130^o.

Vì 130^o > 90^o nên $\widehat{xOy}$ > 90^o.

Vậy $\widehat{xOy}$ = 130^o và $\widehat{xOy}$ > 90^o.

Toán lớp 6 trang 91 Bài 1: Hãy vẽ một hình vuông và hai đường chéo của hình vuông đó. Theo em, góc tạo bởi một đường chéo và một cạnh hình vuông bằng bao nhiêu độ? Hãy đo để kiểm tra.

Bây giờ hãy vẽ một hình vuông với cạnh lớn hoặc nhỏ hơn hình vuông đã vẽ. Hãy đo góc tạo bởi đường chéo và một cạnh hình vuông. Kết quả có thay đổi không?

Lời giải:

* Hình vuông ABCD và hai đường chéo AC, BD như trên hình vẽ: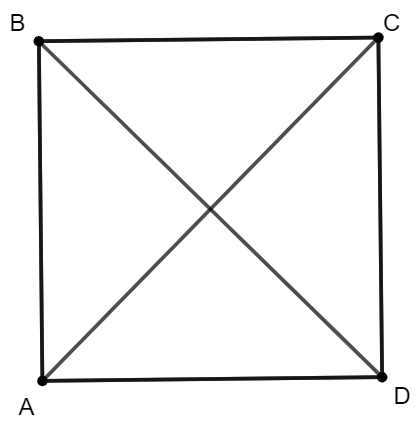

Ta có thể chọn một cạnh và một đường chéo bất kỳ của hình vuông ABCD.

Dự đoán: góc tạo bởi một đường chéo và một cạnh hình vuông bằng 45 độ. 

Giả sử xét cạnh AD và đường chéo AC. Ta đo góc CAD:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh A của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh AD) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh AC. Ta thấy cạnh AC đi qua vạch chỉ số 45 trên thước đo góc.

Do đó, $\widehat{CAD}$ = 45^o.

Vậy góc tạo bởi một đường chéo và một cạnh hình vuông ABCD bằng 45^o.

* Em có thể vẽ một hình vuông có cạnh lớn hơn hay nhỏ hơn hình vuông đã vẽ.

Giả sử hình vuông MNPQ có cạnh lớn hơn cạnh của hình vuông ABCD như hình vẽ:

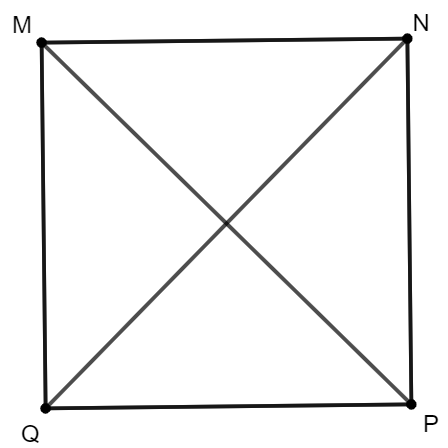
Ta thực hiện đo góc tạo bởi một đường chéo và một cạnh hình vuông MNPQ.

Giả sử xét cạnh QP và đường chéo QN. Ta đo góc PQN:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh Q của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh QP) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh QN. Ta thấy cạnh QN đi qua vạch chỉ số 45 trên thước đo góc.

Do đó, $\widehat{PQN}$ = 45^o.

Vậy góc tạo bởi một đường chéo và một cạnh hình vuông MNPQ bằng 45^o.

Số đo góc tạo bởi một đường chéo và một cạnh của mỗi hình vuông đều cho kết quả không đổi, đều bằng 45^o.

Toán lớp 6 trang 91 Bài 2: Góc tạo bởi kim phút và kim giờ tại thời điểm 9 giờ, 10 giờ, 6 giờ, 5 giờ lần lượt là bao nhiêu độ?

Lời giải:

Khi hai kim chỉ hai số liền kề nhau trên đồng hồ sẽ tạo thành góc 30^o. Chẳng hạn: Khi hai kim đồng hồ lần lượt chỉ số 1 và số 2 thì góc tạo bởi hai kim này là 30^o.

- Tại thời điểm 9 giờ thì kim giờ chỉ số 9 và kim phút chỉ số 12.

Khi đó, góc tạo bởi kim giờ và kim phút lúc này là: 3 . 60^o = 90^o.

- Tại thời điểm 10 giờ thì kim giờ chỉ số 10 và kim phút chỉ số 12.

Khi đó, góc tạo bởi kim giờ và kim phút lúc này là: 2 . 30^o = 60^o.

- Tại thời điểm 6 giờ thì kim giờ chỉ số 6 và kim phút chỉ số 12.

Khi đó, góc tạo bởi kim giờ và kim phút lúc này là: 6 . 30^o = 180^o.

- Tại thời điểm 5 giờ thì kim giờ chỉ số 5 và kim phút chỉ số 12.

Khi đó, góc tạo bởi kim giờ và kim phút lúc này là: 5 . 30^o = 150^o.

Vậy góc tạo bởi kim phút và kim giờ tại thời điểm 9 giờ, 10 giờ, 6 giờ, 5 giờ lần lượt là: 90^o, 60^o, 180^o, 150^o.

(Ngoài ra, ta có thể làm theo cách khác: Chỉnh kim đồng hồ về số giờ cần đo rồi dùng thước đo góc để đo các góc trên).

Toán lớp 6 trang 91 Bài 3: Quan sát các góc ở hình bên, dự đoán số đo gần đúng của các góc. Sau đó dùng thước đo góc để kiểm tra lại kết quả đó.

Lời giải:

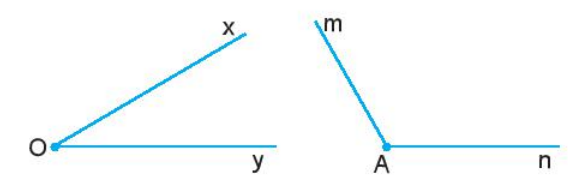
* Dự đoán số đo của các góc trong hình trên như sau:

- Hình thứ nhất: $\widehat{xOy}$ = 30^o;

- Hình thứ hai: $\widehat{mOn}$ = 130^o.

* Dùng thước đo góc để kiểm tra hai góc trên ta được:

• Đo góc xOy:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Oy) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh Ox. Ta thấy cạnh Ox đi qua vạch chỉ số 30 trên thước đo góc.

Do đó, $\widehat{xOy}$ = 30^o (dự đoán trên đúng).

• Đo góc mOn:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh On) đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Cạnh còn lại của góc là cạnh Om. Ta thấy cạnh Om đi qua vạch chỉ số 120 trên thước đo góc.

Do đó, $\widehat{mOn}$ = 120^o (dự đoán trên sai).

Vậy $\widehat{xOy}$ = 30^o, $\widehat{mOn}$ = 120^o.

Toán lớp 6 trang 91 Bài 4: Hãy kể tên các đồ vật trong thực tiễn có hình ảnh góc nhọn, góc vuông góc tù.

Lời giải:

* Hình ảnh góc nhọn: Hai kim của đồng hồ lúc 8 giờ.

* Hình ảnh góc vuông.

- Góc bàn hình chữ nhật:

- Góc tường nhà:

Hình ảnh góc tù:  Hai kim của đồng hồ lúc 5 giờ.

Xem thêm lời giải bài tập Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác: