Giải Toán 12 trang 35 Tập 1 Chân trời sáng tạo

Giải Toán 12 trang 35 Tập 1

Thực hành 4 trang 35 Toán 12 Tập 1: Xét một vật thật đặt trước thấu kính hội tụ có tiêu cự f > 0. Gọi d là khoảng cách từ vật đến thấu kính (d > 0), d' là khoảng cách từ thấu kính đến ảnh (ảnh thật thì d' > 0, ảnh ảo thì d' < 0). Ta có công thức:

$\frac{1}{f}=\frac{1}{d}+\frac{1}{d^{\text{'}}}$ hay $d^{\text{'}}=\frac{df}{d-f}$.

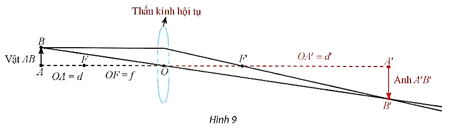
(Vật lí 11, Nhà xuất bản Giáo dục Việt Nam, 2012, trang 182, 187).

Xét trường hợp f = 3, đặt x = d, y = d'. Ta có hàm số $y=\frac{3x}{x-3}$ và x ≠ 3.

a) Khảo sát và vẽ đồ thị của hàm số trên.

b) Dựa vào đồ thị hàm số trên, hãy cho biết vị trí của vật để ảnh của vật là: ảnh thật, ảnh ảo.

c) Khi vật tiến gần đến tiêu điểm thì ảnh thay đổi như thế nào?

Lời giải:

a) Vì d > 0 nên với x = d thì x > 0.

Xét hàm số $y=\frac{3x}{x-3}$ với x > 0 và x ≠ 3.

1. Tập xác định: D = (0; 3) ∪ (3; + ∞).

2. Sự biến thiên:

● Chiều biến thiên:

Đạo hàm y' = $\frac{-9}{{\left(x-3\right)}^2}$. Vì y' < 0 với mọi x > 0 và x ≠ 3 nên hàm số nghịch biến trên mỗi khoảng (0; 3) và (3; + ∞).

● Tiệm cận:

Ta có $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{3x}{x-3}=3$. Suy ra đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số.

Ta có $\underset{x\to 3^{-}}{\lim }y=\underset{x\to 3^{-}}{\lim }\frac{3x}{x-3}=-\infty ;\underset{x\to 3^{+}}{\lim }y=\underset{x\to 3^{+}}{\lim }\frac{3x}{x-3}=+\infty$. Suy ra đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số.

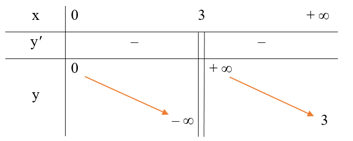
● Bảng biến thiên:

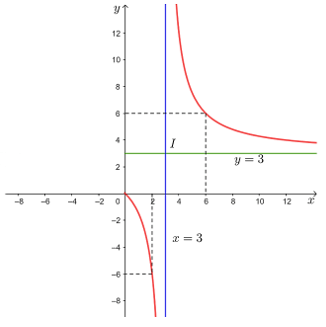
3. Đồ thị:

Đồ thị hàm số đi qua điểm (2; – 6) và điểm (6; 6).

Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.

b)

● Để vật là ảnh thật thì d' > 0, tức là y > 0.

Quan sát đồ thị hàm số $y=\frac{3x}{x-3}$, ta thấy trên khoảng (3; + ∞), đồ thị hàm số nằm phía trên trục Ox nên y > 0 trên khoảng này. Vậy với x > 3, tức d > 3 hay khoảng cách từ vật đến thấy kính lớn hơn 3 thì ảnh của vật là ảnh thật.

● Để vật là ảnh ảo thì d' < 0, tức là y < 0.

Quan sát đồ thị hàm số $y=\frac{3x}{x-3}$, ta thấy trên khoảng (0; 3), đồ thị hàm số nằm phía dưới trục Ox nên y < 0 trên khoảng này. Vậy với x ∈ (0; 3), tức d ∈ (0; 3) hay khoảng cách từ vật đến thấu kính lớn hơn 0 và nhỏ hơn 3 thì ảnh của vật là ảnh ảo.

c) Khi vật tiến gần đến tiêu điểm, tức vị trí A tiến gần đến vị trí F, thì khoảng cách AF dần tiến tới 0, hay d – f → 0, suy ra d → f, tức là x → 3.

Thực hành 5 trang 35 Toán 12 Tập 1: Người ta muốn chế tạo một chiếc hộp hình hộp chữ nhật có thể tích 500 cm3 với yêu cầu dùng ít vật liệu nhất.

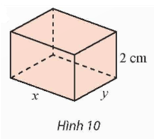
Chiều cao hộp phải là 2 cm, các kích thước khác là x, y với x > 0 và y > 0.

a) Hãy biểu thị y theo x.

b) Chứng tỏ rằng diện tích toàn phần của chiếc hộp là:

$S\left(x\right)=500+4x+\frac{1000}{x}$.

c) Lập bảng biến thiên của hàm số S(x) trên khoảng (0; + ∞).

d) Kích thước của hộp là bao nhiêu thì dùng ít vật liệu nhất? (Làm tròn kết quả đến hàng phần mười.)

Lời giải:

a) Thể tích của hình hộp chữ nhật cần chế tạo là: V = 2xy (cm³).

Theo bài ra ta có V = 500 cm³, khi đó 2xy = 500, suy ra y = $\frac{250}{x}$.

b) Diện tích xung quanh của chiếc hộp là

S_xq = 2(x + y) ∙ 2 = 4(x + y) (cm²).

Diện tích toàn phần của chiếc hộp là

S_tp = S_xq + 2S_đ = 4(x + y) + 2xy (cm²)

Lại có y = $\frac{250}{x}$ nên S_tp = $4\left(x+\frac{250}{x}\right)+2x\cdot \frac{250}{x}=4x+\frac{1000}{x}+500$.

Vậy diện tích toàn phần của chiếc hộp là $S\left(x\right)=500+4x+\frac{1000}{x}$.

c) Xét hàm số $S\left(x\right)=500+4x+\frac{1000}{x}$ với x ∈ (0; + ∞).

Ta có S'(x) = 4 – $\frac{1000}{x^2}$;

Trên khoảng (0; + ∞), S'(x) = 0 khi x = $5\sqrt{10}$.

Ta có $\underset{x\to 0^{+}}{\lim }S\left(x\right)=\underset{x\to 0^{+}}{\lim }\left(500+4x+\frac{1000}{x}\right)=+\infty$;

$\underset{x\to +\infty }{\lim }S\left(x\right)=\underset{x\to +\infty }{\lim }\left(500+4x+\frac{1000}{x}\right)=+\infty$

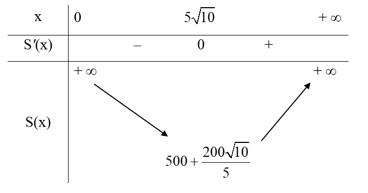
Bảng biến thiên:

d) Để dùng ít vật liệu nhất thì diện tích toàn phần của chiếc hộp phải nhỏ nhất.

Căn cứ vào bảng biến thiên ở câu c), ta thấy hàm số S(x) đạt giá trị nhỏ nhất bằng $500+\frac{200\sqrt{10}}{5}$ tại x = $5\sqrt{10}$.

Với x = $5\sqrt{10}$, ta có y = $\frac{250}{5\sqrt{10}}=5\sqrt{10}$.

Vậy kích thước 3 cạnh của chiếc hộp là 2 cm, $5\sqrt{10}$cm, $5\sqrt{10}$cm thì dùng ít vật liệu nhất.

Xem thêm Lời giải bài tập Toán 12 sách Chân trời sáng tạo hay, chi tiết khác:

Giải Toán 12 trang 25 Tập 1

Giải Toán 12 trang 28 Tập 1

Giải Toán 12 trang 30 Tập 1

Giải Toán 12 trang 32 Tập 1

Giải Toán 12 trang 35 Tập 1

Giải Toán 12 trang 36 Tập 1