Nội dung bài viết

    Xem thêm

    Toán 12 (Chân trời sáng tạo) Bài tập cuối chương 2 trang 65

    Với giải bài tập Toán lớp 12 Bài tập cuối chương 2 trang 65 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 12.

    1 1,111 17/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Bài tập cuối chương 2 trang 65

    Câu hỏi trắc nghiệm

    Giải Toán 12 trang 65 Tập 1

    Bài 1 trang 65 Toán 12 Tập 1: Cho điểm M thỏa mãn OM→=2i→+j→. Tọa độ của điểm M là:

    A. M(0; 2; 1).

    B. M(1; 2; 0).

    C. M(2; 0; 1).

    D. M(2; 1; 0).

    Lời giải:

    Đáp án đúng là: D

    Vì OM→=2i→+j→ nên M2;1;0 .

    Bài 2 trang 65 Toán 12 Tập 1: Cho hai điểm A(−1; 2; −3) và B(2; −1; 0). Tọa độ của vectơ AB→ là

    A. AB→=1;−1;1 .

    B. AB→=3;3;−3 .

    C. AB→=1;1;−3 .

    D. AB→=3;−3;3 .

    Lời giải:

    Đáp án đúng là: D

    Ta có AB→=2+1;−1−2;0+3=3;−3;3

    Bài 3 trang 65 Toán 12 Tập 1: Cho hai điểm A(3; −2; 3) và B(−1; 2; 5). Tọa độ trung điểm I của đoạn thẳng AB là

    A. I(−2; 2; 1).

    B. I(1; 0; 4).

    C. I(2; 0; 8).

    D. I(2; −2; −1).

    Lời giải:

    Đáp án đúng là: B

    Tọa độ trung điểm I là

    I3−12;−2+22;3+52 hay I(1;0;4) .

    Bài 4 trang 65 Toán 12 Tập 1: Cho ba điểm A(1; 3; 5), B(2; 0; 1), C(0; 9; 0). Tọa độ trọng tâm G của tam giác ABC là

    A. G(3; 12; 6).

    B. G(1; 5; 2).

    C. G(1; 0; 5).

    D. G(1; 4; 2).

    Lời giải:

    Đáp án đúng là: D

    Tọa độ trung điểm G là

    G1+2+03;3+0+93;5+1+03 hay G(1;4;2).

    Bài 5 trang 65 Toán 12 Tập 1: Cho A(1; 2; −1), B(2; 1; −3), C(−3; 5; 1). Điểm D sao cho ABCD là hình bình hành có tọa độ là

    A. D(−4; 6; 3).

    B. D(−2; 2; 5).

    C. D(−2; 8; −3).

    D. D(−4; 6; −5).

    Lời giải:

    Đáp án đúng là: A

    ABCD là hình bình hành ⇔AB→=DC→ ⇔2−1=−3−xD1−2=5−yD−3+1=1−zD⇔xD=−4yD=6zD=3

    Vậy D(−4; 6; 3).

    Bài 6 trang 65 Toán 12 Tập 1: Gọi α là góc giữa hai vectơ u→=0;−1;0 và v→=3;1;0. Giá trị của α là

    A. α=π6 .

    B. α=π3 .

    C. α=2π3 .

    D. α=π2 .

    Lời giải:

    Đáp án đúng là: C

    Ta có cosα=u→.v→u→.v→=0.3+−1.1+0.0−12.3+1=−12

    Bài 7 trang 65 Toán 12 Tập 1: Cho A(2; −1; 1), B(−1; 3; −1), C(5; −3; 4). Tích vô hướng AB→.BC→ có giá trị là

    A. 48.

    B. −48.

    C. 52.

    D. −52.

    Lời giải:

    Đáp án đúng là: D

    Có AB→=−3;4;−2 , BC→=6;−6;5 .

    Có AB→.BC→=−3.6+4.−6+−2.5=−52 .

    Bài 8 trang 65 Toán 12 Tập 1: Cho hai điểm A(−1; 2; 3), B(1; 0; 2). Tọa độ điểm M thỏa mãn AB→=2MA→ là

    A. M−2;3;72 .

    B. M−2;−3;72 .

    C. M(−2; 3; 7).

    D. M(−4; 6; 7).

    Lời giải:

    Đáp án đúng là: A

    Giả sử M(x; y; z).

    Có AB→=2;−2;−1 và MA→=−1−x;2−y;3−z .

    Vì AB→=2MA→ nên 2=2−1−x−2=22−y−1=23−z ⇔x=−2y=3z=72. Vậy M−2;3;72 .

    Bài tập tự luận

    Bài 9 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, cho hình hộp chữ nhật OABC.O'A'B'C' như Hình 1, biết B'(2; 3; 5).

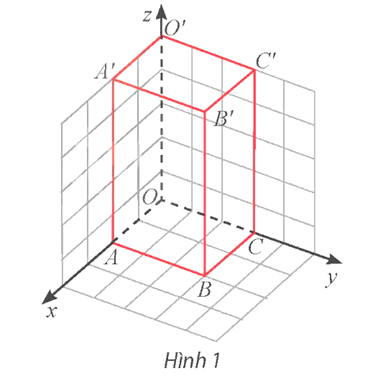
    a) Tìm tọa độ các đỉnh còn lại của hình hộp.

    b) Tính độ dài đường chéo OB' của hình hộp chữ nhật đó.

    Bài 9 trang 65 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    Lời giải:

    a) Dựa vào Hình 1 ta có:

    O(0; 0; 0), A(2; 0; 0), B(2; 3; 0), C(0; 3; 0),

    O'(0; 0; 5), A'(2; 0; 5), B'(2; 3; 5), C'(0; 3; 5).

    b) Có OB'=22+32+52=38 .

    Bài 10 trang 65 Toán 12 Tập 1: Tìm tọa độ của điểm P được biểu diễn trong Hình 2 và tính khoảng cách OP.

    Bài 10 trang 65 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    Lời giải:

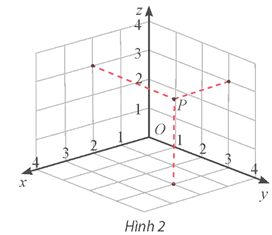
    Ta có P(2; 3; 3).

    Khi đó OP=22+32+32=22 .

    Giải Toán 12 trang 66 Tập 1

    Bài 11 trang 66 Toán 12 Tập 1: Cho u→=2;−5;3 và v→=0;2;−1, w→=1;7;2 . Tìm tọa độ của vectơ a→=u→−4v→−2w→ .

    Lời giải:

    4v→=0;8;−4; 2w→=2;14;4 .

    Có a→=u→−4v→−2w→ = (2 - 0 - 2;- 5 - 8 - 14;3 + 4 - 4) = (0; -27; 3).

    Bài 12 trang 66 Toán 12 Tập 1: Cho ba điểm A(0; 1; 2), B(1; 2; 3), C(1; −2; −5). Gọi M là điểm nằm trên đoạn thẳng BC sao cho MB = 3MC. Tính độ dài đoạn thẳng AM.

    Lời giải:

    Vì M nằm trên đoạn thẳng BC nên MB→ và MC→ ngược hướng.

    Mà MB = 3MC nên MB→=−3MC→ .

    Gọi M(x; y; z). Có MB→=1−x;2−y;3−z và MC→=1−x;−2−y;−5−z .

    Vì MB→=−3MC→ nên 1−x=−31−x2−y=−3−2−y3−z=−3−5−z ⇔x=1y=−1z=−3.

    Vậy M(1; −1; −3).

    Khi đó ta có AM=1−02+−1−12+−3−22=30 .

    Bài 13 trang 66 Toán 12 Tập 1: Cho hai vectơ u→ và v→ tạo với nhau góc 60°. Biết rằng u→=2 và v→=4 . Tính u→+v→ .

    Lời giải:

    Ta có u→+v→2=u→2+2.u→.v→+v→2

    =22+2.u→.v→.cosu→,v→+42

    =22+2.2.4.cos60°+42

    =22+2.2.4.12+42=28

    Do đó u→+v→=28=27 .

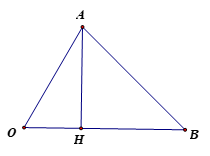
    Bài 14 trang 66 Toán 12 Tập 1: Cho hai điểm A(1; 2; −1), B(0; −2; 3).

    a) Tính độ dài đường cao AH hạ từ đỉnh A của tam giác OAB với O là gốc tọa độ.

    b) Tính diện tích tam giác OAB.

    Lời giải:

    Bài 14 trang 66 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    a) Gọi H(x; y; z) là chân đường cao hạ từ A xuống OB.

    Ta có BH→=x;y+2;z−3 ; BO→=0;2;−3

    Vì H ∈ OB và BH→ và BO→ cùng phương nên BH→=kBO→

    ⇔x=0y+2=2kz−3=−3k⇔x=0y=2k−2z=−3k+3

    Do đó H(0; 2k – 2; −3k + 3).

    Suy ra AH→=−1;2k−2−2;−3k+3+1 hay AH→=−1;2k−4;−3k+4 .

    Vì AH→⊥BO→ nên AH→.BO→=0

    ⇔−1.0+2k−4.2+−3k+4.−3=0

    ⇔k=2013

    Suy ra H0;1413;−2113 , AH→=−1;−1213;−813

    Độ dài đường cao AH là AH→=−12+−12132+−8132=37713.

    b) Ta có BO→=0+22+−32=13 .

    Do đó SΔABC=12.BO.AH=12.13.37713 =292 .

    Bài 15 trang 66 Toán 12 Tập 1: Cho biết máy bay A đang bay với vectơ vận tốc a→=300;200;400 (đơn vị: km/h). Máy bay B bay cùng hướng và có tốc độ gấp ba lần tốc độ của máy bay A.

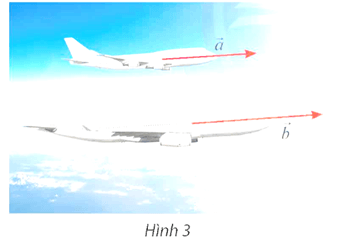
    a) Tìm tọa độ vectơ vận tốc b→ của máy bay B.

    b) Tính tốc độ của máy bay B.

    Bài 15 trang 66 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    Lời giải:

    a) Có b→=3a→=900;600;1200 .

    b) Tốc độ của máy bay B là:

    b→=9002+6002+12002≈1615,55 km/h

    Bài 16 trang 66 Toán 12 Tập 1: Cho biết bốn đoạn thẳng nối từ một đỉnh của tứ diện đến trọng tâm mặt đối diện luôn cắt nhau tại một điểm gọi là trọng tâm của tứ diện đó.

    Một phân tử metan CH4 được cấu tạo bởi bốn nguyên tử hydrogen ở các đỉnh của một tứ diện đều và một nguyên tử carbon ở trọng tâm của tứ diện.

    Góc liên kết là góc tạo bởi liên kết H – C – H là góc giữa các đường nối nguyên tử carbon với hai trong số các nguyên tử hydrogen. Chứng minh rằng góc liên kết này gần bằng 109,5°.

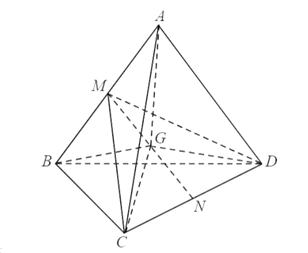
    Bài 16 trang 66 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    Lời giải:

    Bài 16 trang 66 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    Gọi G là trọng tâm của tứ diện đều ABCD.

    Đặt a→=GA→,b→=GB→,c→=GC→,d→=GD→

    Ta có a→=b→=c→=d→ và a→.b→=a→.c→=a→.d→=b→.c→=b→.d→=c→.d→

    Ta có a→+b→+c→+d→=GA→+GB→+GC→+GD→=0→

    ⇒a→+b→+c→+d→2=0

    Bài 16 trang 66 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    ⇒4a→2+12.a→.b→=0

    ⇒a→.b→a→2=−13

    ⇒cosa→,b→=−13

    ⇒a→,b→≈109,5°

    Vậy góc liên kết gần bằng 109,5°.

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 3: Biểu thức toạ độ của các phép toán vectơ

    Bài 1: Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm

    Bài 2: Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

    Bài tập cuối chương 3 trang 84

    Bài 1: Vẽ đồ thị hàm số bằng phần mềm Geogebra

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,111 17/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: