Khảo sát và vẽ đồ thị của các hàm số sau: a) y = x+1/x-1; b) y = 2x/3x-1

Lời giải Thực hành 2 trang 30 Toán 12 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12.

1 1,889 14/10/2024

Trang trước

Trang sau

Giải Toán 12 Chân trời sáng tạo Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản

Thực hành 2 trang 30 Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau:

a) $y = \frac{x + 1}{x - 1}$ ;

b) $y = \frac{2 x}{3 x - 1}$ ;

c) $y = \frac{5 + x}{2 - x}$ .

*Lý thuyết liên quan

Sơ đồ khảo sát hàm số y = f(x):

Bước 1: Tìm tập xác định của hàm số.

Bước 2: Khảo sát sự biến thiên của hàm số:

- Tính đạo hàm y'. Tìm các điểm tại đó y' bằng 0 hoặc đạo hàm không tồn tại.

- Xét dấu y' để chỉ ra các khoảng đơn điệu của hàm số.

- Tìm cực trị của hàm số.

- Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số (nếu có).

- Lập bảng biến thiên của hàm số.

Bước 3: Vẽ đồ thị của hàm số dựa vào bảng biến thiên.

Chú ý:

Khi vẽ đồ thị, nên xác định thêm một số điểm đặc biệt của đồ thị, chẳng hạn tìm giao điểm của đồ thị với các trục tọa độ (khi có và việc tìm không quá phức tạp). Ngoài ra, cần lưu ý đến tính đối xứng của đồ thị (đối xứng tâm, đối xứng trục).

*Lời giải:

a) $y = \frac{x + 1}{x - 1}$

1. Tập xác định: D = ℝ\{1}.

2. Sự biến thiên:

● Chiều biến thiên:

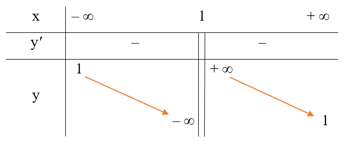
Đạo hàm y' = $\frac{- 2}{{(x - 1)}^{2}}$ . Vì y' < 0 với mọi x ≠ 1 nên hàm số nghịch biến trên mỗi khoảng (– ∞; 1) và (1; + ∞).

● Tiệm cận:

Ta có $\lim_{x \to - \infty} y = \lim_{x \to - \infty} \frac{x + 1}{x - 1} = 1; \lim_{x \to + \infty} y = \lim_{x \to + \infty} \frac{x + 1}{x - 1} = 1$ . Suy ra đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.

Ta có $\lim_{x \to 1^{-}} y = \lim_{x \to 1^{-}} \frac{x + 1}{x - 1} = - \infty; \lim_{x \to 1^{+}} y = \lim_{x \to 1^{+}} \frac{x + 1}{x - 1} = + \infty$ . Suy ra đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

● Bảng biến thiên:

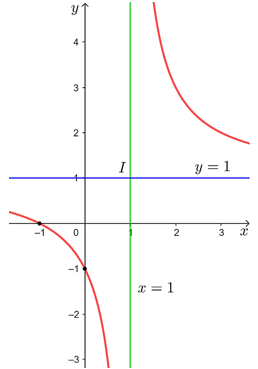
Thực hành 2 trang 30 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

3. Đồ thị:

Đồ thị hàm số giao với trục Ox tại điểm (– 1; 0), giao với trục Oy tại điểm (0; – 1).

Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.

Thực hành 2 trang 30 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

Tâm đối xứng của đồ thị hàm số là điểm I(1; 1). Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 1 và y = 1.

b) $y = \frac{2 x}{3 x - 1}$

1. Tập xác định: D = ℝ\ $\{\frac{1}{3}\}$ .

2. Sự biến thiên:

● Chiều biến thiên:

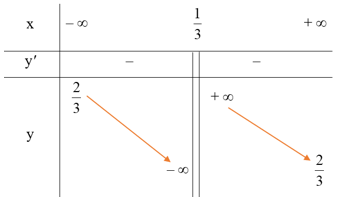
Đạo hàm y' = $\frac{- 2}{{(3 x - 1)}^{2}}$ . Vì y' < 0 với mọi x ≠ $\frac{1}{3}$ nên hàm số nghịch biến trên mỗi khoảng $(- \infty; \frac{1}{3})$ và $(\frac{1}{3}; + \infty)$ .

● Tiệm cận:

Ta có $\lim_{x \to - \infty} y = \lim_{x \to - \infty} \frac{2 x}{3 x - 1} = \frac{2}{3}; \lim_{x \to + \infty} y = \lim_{x \to + \infty} \frac{2 x}{3 x - 1} = \frac{2}{3}$ . Suy ra đường thẳng y = $\frac{2}{3}$ là tiệm cận ngang của đồ thị hàm số.

Ta có $\lim_{x \to {\frac{1}{3}}^{-}} y = \lim_{x \to {\frac{1}{3}}^{-}} \frac{2 x}{3 x - 1} = - \infty; \lim_{x \to {\frac{1}{3}}^{+}} y = \lim_{x \to {\frac{1}{3}}^{+}} \frac{2 x}{3 x - 1} = + \infty$ . Suy ra đường thẳng x = $\frac{1}{3}$ là tiệm cận đứng của đồ thị hàm số.

● Bảng biến thiên:

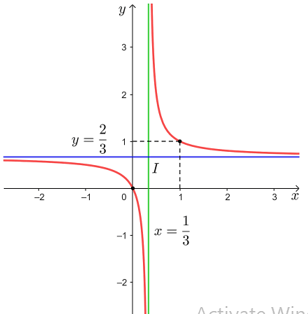
Thực hành 2 trang 30 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

3. Đồ thị:

Đồ thị hàm số đi qua gốc tọa độ O(0; 0) và điểm (1; 1).

Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.

Thực hành 2 trang 30 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

Tâm đối xứng của đồ thị hàm số là điểm I $(\frac{1}{3}; \frac{2}{3})$ . Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = $\frac{1}{3}$ và y = $\frac{2}{3}$ .

c) $y = \frac{5 + x}{2 - x}$

1. Tập xác định: D = ℝ\{2}.

2. Sự biến thiên:

● Chiều biến thiên:

Đạo hàm y' = $\frac{7}{{(2 - x)}^{2}}$ . Vì y' > 0 với mọi x ≠ 2 nên hàm số đồng biến trên mỗi khoảng (– ∞; 2) và (2; + ∞).

● Tiệm cận:

Ta có $\lim_{x \to - \infty} y = \lim_{x \to - \infty} \frac{5 + x}{2 - x} = - 1; \lim_{x \to + \infty} y = \lim_{x \to + \infty} \frac{5 + x}{2 - x} = - 1$ . Suy ra đường thẳng y = – 1 là tiệm cận ngang của đồ thị hàm số.

Ta có $\lim_{x \to 2^{-}} y = \lim_{x \to 2^{-}} \frac{5 + x}{2 - x} = + \infty; \lim_{x \to 2^{+}} y = \lim_{x \to 2^{+}} \frac{5 + x}{2 - x} = - \infty$ . Suy ra đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.

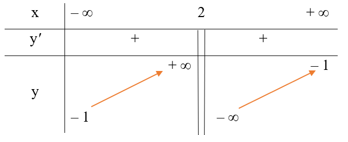
● Bảng biến thiên:

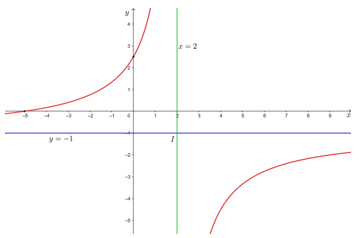
Thực hành 2 trang 30 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

3. Đồ thị:

Đồ thị hàm số giao với trục Ox tại điểm (– 5; 0), giao với trục Oy tại điểm $(0; \frac{5}{2})$ .

Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.

Thực hành 2 trang 30 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

Tâm đối xứng của đồ thị hàm số là điểm I(2; – 1). Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 2 và y = – 1.

Xem thêm các bài toán hay, chi tiết khác

Lý thuyết Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số- Kết nối tri thức

Giải Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Hoạt động khởi động trang 25 Toán 12 Tập 1: Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình v (km/h) theo công thức...

Hoạt động khám phá trang 25 Toán 12 Tập 1: Cho hàm số y = – x² + 4x – 3. a) Lập bảng biến thiên. b) Vẽ đồ thị của hàm số.

Thực hành 1 trang 28 Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: a) y = – 2x³ – 3x² + 1; b) y = x³ + 3x² + 3x + 2.

Thực hành 2 trang 30 Toán 12 Tập 1: Khảo sát và vẽ đồ thị của các hàm số sau: a) $y = \frac{x + 1}{x - 1}$ ; b) $y = \frac{2 x}{3 x - 1}$ ; c) $y = \frac{5 + x}{2 - x}$ .