Giải Toán 11 trang 27 Tập 2 Cánh diều

Với giải bài tập Toán 11 trang 27 Tập 2 trong Bài 1: Phép tính lũy thừa với số mũ thực sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 27 Tập 2.

1 183 lượt xem

Giải Toán 11 trang 27 Tập 2

Câu hỏi khởi động trang 27 Toán 11 Tập 2: Ở các lớp dưới, ta đã làm quen với phép tính lũy thừa với số mũ tự nhiên của một số thực và các tính chất của phép tính lũy thừa đó. Những khái niệm lũy thừa với số mũ nguyên, số mũ hữu tỉ và số mũ thực của một số thực được xây dựng như thế nào? Những phép lũy thừa đó có tính chất gì?

Lời giải:

– Những khái niệm lũy thừa với số mũ nguyên, số mũ hữu tỉ và số mũ thực của một số thực được xây dựng dựa trên lũy thừa bậc n của a, kí hiệu là aⁿ, là tích của n thừa số a:

aⁿ = a.a.a...a (n thừa số a) với n là số nguyên dương.

Số a được gọi là cơ số, n được gọi là số mũ.

– Tính chất của lũy thừa mà ta đã học ở các lớp dưới:

⦁ a^m . aⁿ = a^m+n;

⦁ $\frac{a^{m}}{a^{n}} = a^{m - n};$

⦁ ${(a^{m})}^{n} = a^{m . n};$

⦁ (a . b)^m = a^m . b^m;

⦁ ${(\frac{a}{b})}^{m} = \frac{a^{m}}{b^{m}};$

⦁ Với a > 1 thì a^m > aⁿ ⇔ m > n;

⦁Với 0 < a < 1 thì a^m > aⁿ ⇔ m < n.

I. Phép tính lũy thừa với số mũ hữu tỷ

Hoạt động 1 trang 27 Toán 11 Tập 2:

a) Cho n là một số nguyên dương. Với a là số thực tùy ý, nêu định nghĩa lũy thừa bậc n của a.

b) Với a là số thực tùy ý khác 0, nêu quy ước xác định lũy thừa bậc 0 của a.

Lời giải:

a) Lũy thừa bậc n của a, kí hiệu là aⁿ, là tích của n thừa số a: aⁿ = a.a.a...a (n thừa số a) với n là số nguyên dương.

Số a được gọi là cơ số, n được gọi là số mũ.

b) Quy ước xác định lũy thừa bậc 0 của a (với a khác 0) là: a⁰ =1.

Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

Giải Toán 11 trang 27 Tập 2

Giải Toán 11 trang 28 Tập 2

Giải Toán 11 trang 29 Tập 2

Giải Toán 11 trang 30 Tập 2

Giải Toán 11 trang 31 Tập 2

Giải Toán 11 trang 32 Tập 2

Giải Toán 11 trang 33 Tập 2

Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

Câu hỏi khởi động trang 27 Toán 11 Tập 2: Ở các lớp dưới, ta đã làm quen với phép tính lũy thừa với số mũ tự nhiên của một số thực và các tính chất của phép tính lũy thừa đó...

Hoạt động 1 trang 27 Toán 11 Tập 2: a) Cho n là một số nguyên dương. Với a là số thực tùy ý, nêu định nghĩa lũy thừa bậc n của a...

Luyện tập 1 trang 28 Toán 11 Tập 2: Tính giá trị của biểu thức: $M = {(\frac{1}{3})}^{12} \cdot {(\frac{1}{27})}^{- 5} + {(0,4)}^{- 4} \cdot 25^{- 2} \cdot {(\frac{1}{32})}^{- 1} .$ ..

Hoạt động 2 trang 28 Toán 11 Tập 2: a) Với a là số thực không ân, nêu định nghĩa căn bậc hai của a...

Luyện tập 2 trang 28 Toán 11 Tập 2: Các số 2 và –2 có phải là căn bậc 6 của 64 hay không...

Hoạt động 3 trang 29 Toán 11 Tập 2: a) Với mỗi số thực a, so sánh: $\sqrt{a^{2}}$ và |a|; $\sqrt[3]{a^{3}}$ và a. b) Cho a, b là hai số thực dương. So sánh $\sqrt{a \cdot b}$ và $\sqrt{a} \cdot \sqrt{b} .$ ..

Luyện tập 3 trang 29 Toán 11 Tập 2: Rút gọn mỗi biểu thức sau: a) $\sqrt[3]{\frac{125}{64}} . \sqrt[4]{81};$ b) $\frac{\sqrt[5]{98} . \sqrt[5]{343}}{\sqrt[5]{64}} .$ ..

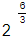
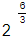
Hoạt động 4 trang 29 Toán 11 Tập 2: Thực hiện các hoạt động sau: a) So sánh và 2²; b) So sánh và $\sqrt[3]{2^{6}} .$ ..

Luyện tập 4 trang 30 Toán 11 Tập 2: Rút gọn mỗi biểu thức: $N = \frac{x^{\frac{4}{3}} y + x y^{\frac{4}{3}}}{\sqrt[3]{x} + \sqrt[3]{y}} (x > 0, y > 0) .$ ..

Hoạt động 5 trang 30 Toán 11 Tập 2: Xét số vô tỉ $\sqrt{2} = 1,414213562...$ Xét dãy số hữu tỉ r₁ = 1; r₂ = 1,4; r₃ = 1,41; r₄ = 1,414; r₅ = 1,4142; r₆ = 1,41421; ...và $\lim r_{n} = \sqrt{2} .$ ...

Luyện tập 5 trang 31 Toán 11 Tập 2: So sánh $10^{\sqrt{2}}$ và 10...

Hoạt động 6 trang 31 Toán 11 Tập 2: Nêu những tính chất của phép tính lũy thừa với số mũ nguyên của một số thực dương...

Luyện tập 6 trang 32 Toán 11 Tập 2: Không sử dụng máy tính cầm tay, hãy so sánh các số $2^{2 \sqrt{3}}$ và $2^{3 \sqrt{2}} .$ ..

Luyện tập 7 trang 32 Toán 11 Tập 2: Dùng máy tính cầm tay để tính (làm tròn kết quả đến hàng phần trăm): a) ${(- 2,7)}^{- 4};$ b) ${(\sqrt{3} - 1)}^{\sqrt[3]{4} + 1} .$ ..

Bài 1 trang 33 Toán 11 Tập 2: Tính: a) ${(\frac{1}{256})}^{- 0,75} + {(\frac{1}{27})}^{- \frac{4}{3}};$ b) ${(\frac{1}{49})}^{- 1,5} - {(\frac{1}{125})}^{- \frac{2}{3}};$ ...

Bài 2 trang 33 Toán 11 Tập 2: Cho a, b là những số thực dương. Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ: a) $a^{\frac{1}{3}} \cdot \sqrt{a};$ b) $b^{\frac{1}{2}} \cdot b^{\frac{1}{3}} \cdot \sqrt[6]{b};$ c) $a^{\frac{4}{3}} : \sqrt[3]{a};$ d) $\sqrt[3]{b} : b^{\frac{1}{6}} .$ ...

Bài 3 trang 33 Toán 11 Tập 2: Rút gọn mỗi biểu thức sau: a) $\frac{a^{\frac{7}{3}} - a^{\frac{1}{3}}}{a^{\frac{4}{3}} - a^{\frac{1}{3}}} (a > 0; a \neq 1);$ b) $\sqrt[3]{\sqrt{a^{12} b^{6}}} (a > 0, b > 0) .$ ...

Bài 4 trang 33 Toán 11 Tập 2: Viết các số sau theo thứ tự tăng dần: a) $1^{1,5}; 3^{- 1}; {(\frac{1}{2})}^{- 2};$ b) $2022^{0}; {(\frac{4}{5})}^{- 1}; 5^{\frac{1}{2}} .$ ...

Bài 5 trang 33 Toán 11 Tập 2: Không sử dụng máy tính cầm tay, hãy so sánh các số sau:

a) $6^{\sqrt{3}}$ và 36; b) ${(0,2)}^{\sqrt{3}}$ và ${(0,2)}^{\sqrt{5}} .$ ...

Bài 6 trang 33 Toán 11 Tập 2: Định luật thứ ba của Kepler về quỹ đạo chuyển động cho biết cách ước tính khoảng thời gian P (tính theo năm Trái Đất)...

Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 5 trang 25

Bài 2: Phép tính lôgarit

Bài 3: Hàm số mũ. Hàm số lôgarit

Bài 4: Phương trình, bất phương trình mũ và lôgarit

Bài tập cuối chương 6 trang 55

1 183 lượt xem

Xem thêm các chương trình khác: