Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 38 Tập 1 Cánh diều

    Với giải bài tập Toán lớp 10 trang 38 Tập 1 trong Bài 1: Hàm số và đồ thị sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 38 Tập 1.

    1 304 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 38 Tập 1

    Bài 3 trang 38 Toán lớp 10 Tập 1: Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có khối lượng đến 250 g như trong bảng sau:

    Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam

    a) Số tiền dịch vụ thư cơ bản phải trả y (đồng) có là hàm số của khối lượng thư cơ bản x (g) hay không? Nếu đúng, hãy xác định những công thức tính y. 

    b) Tính số tiền phải trả khi bạn Dương gửi thư có khối lượng 150g, 200g. 

    Lời giải:

     a) Quan sát bảng số liệu, ta thấy: Với mỗi khối lượng thư cơ bản x (g) có một và chỉ một mức cước tương ứng hay số tiền dịch vụ cơ bản phải trả y (đồng) tương ứng nên y là hàm số của x.

    Ta có:

    + Nếu 0 < x ≤ 20 thì y = 4 000.

    + Nếu 20 < x ≤ 100 thì y = 6 000.

    + Nếu 100 < x ≤ 250 thì y = 8 000.

    Khi đó, ta có công thức xác định y như sau: 

    y=4 000      nê'u   0<x≤206 000      nê'u   20<x≤1008 000        nê'u  100<x≤250 .

    b) Nếu bạn Dương gửi thư có khối lượng x = 150 g mà 100 < 150 < 250 nên tiền cước phải trả là y = 8 000 đồng.

    Nếu bạn Dương gửi thư có khối lượng x = 200 g mà 100 < 200 < 250 nên tiền cước phải trả là y = 8 000 đồng.

    Số tiền phải trả khi bạn Dương gửi thư có khối lượng 150 g, 200 g là:

    8 000 + 8 000 = 16 000 (đồng).

    Vậy tổng số tiền bạn Dương phải trả khi gửi thư có khối lượng 150g và 200g là 16 000 đống.

    Bài 4 trang 38 Toán lớp 10 Tập 1: Cho hàm số y = – 2x2.

    a) Tìm những điểm thuộc đồ thị hàm số có hoành độ lần lượt bằng – 2; 3 và 10.

    b) Tìm những điểm thuộc đồ thị hàm số có tung độ bằng – 18. 

    Lời giải:

    a) Điểm có hoành độ bằng – 2 hay x = – 2 thì tung độ y = (– 2) . (– 2)2 = – 8.

    Điểm có hoành độ bằng 3 hay x = 3 thì tung độ y = (– 2) . 32 = – 18.

    Điểm có hoành độ bằng 10 hay x = 10 thì tung độ y = (– 2) . 102 = – 200. 

    Vậy các điểm cần tìm có tọa độ là (– 2; – 8), (3; – 18) và (10; – 200). 

    b) Điểm có tung độ bằng – 18 hay y = – 18.

    Khi đó: – 2x2 = – 18 ⇔ x2 = 9 ⇔ x = ± 3. 

    Vậy các điểm thuộc đồ thị hàm số có tung độ bằng – 18 là (3; – 18) và (– 3; – 18).

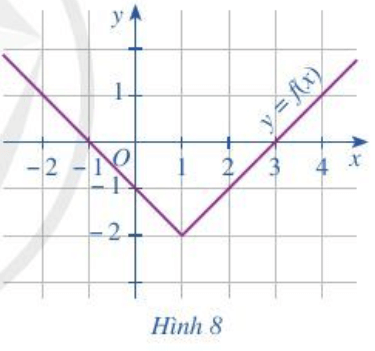
    Bài 5 trang 38 Toán lớp 10 Tập 1: Cho đồ thị hàm số y = f(x) như Hình 8.

    Cho đồ thị hàm số y = f(x) như Hình 8. Trong các điểm có tọa độ (1; – 2), (0; 0), (2; – 1)

    a) Trong các điểm có tọa độ (1; – 2), (0; 0), (2; – 1), điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số? 

    b) Xác định f(0); f(3).

    c) Tìm điểm thuộc đồ thị hàm số có tung độ bằng 0. 

    Lời giải:

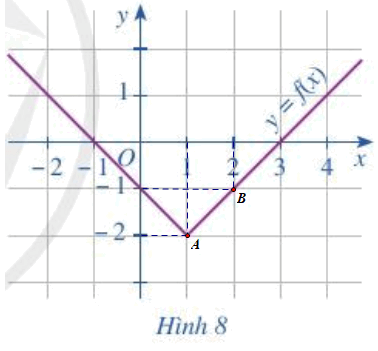
     a) Xác định các điểm A(1; – 2), O(0; 0) và B(2; – 1) lên mặt phẳng tọa độ ở Hình 8:

    Cho đồ thị hàm số y = f(x) như Hình 8. Trong các điểm có tọa độ (1; – 2), (0; 0), (2; – 1)

    Dựa vào hình vẽ ta thấy:

    Đồ thị hàm số y = f(x) không đi qua điểm O(0; 0) nên điểm O(0; 0) không thuộc đồ thị hàm số đã cho.

    Đồ thị hàm số đi qua hai điểm A, B nên hai điểm A(1; – 2) và B(2; – 1) thuộc đồ thị hàm số đã cho.

    Vậy điểm có tọa độ (1; -2) và (2; -1) thuộc đồ thị hàm số và điểm có tọa độ (0; 0) không thuộc đồ thị hàm số đã cho.

    b) Tại x = 0 dóng đường thẳng vuông góc với trục Ox cắt đồ thị hàm số tại điểm có tọa độ (0; -1) nên f(0) = -1.

    Tại x = 3 dóng đường thẳng vuông góc với trục Ox cắt đồ thị hàm số tại điểm có tọa độ (3; 0) nên f(3) = 0.

    Vậy f(0) = – 1; f(3) = 0.

    c) Điểm thuộc đồ thị có tung độ bằng 0 hay y = 0

    Tại điểm có y = 0 dóng đường thẳng vuông góc với trục tung cắt đồ thị tại điểm có tọa độ (3; 0).

    Vậy điểm thuộc đồ thị có tung độ bằng 0 là điểm có tọa độ (3; 0).

    Bài 6 trang 38 Toán lớp 10 Tập 1: Cho hàm số y=1x. Chứng tỏ hàm số đã cho: 

    a) Nghịch biến trên khoảng (0; + ∞);

    b) Nghịch biến trên khoảng (– ∞; 0).

    Lời giải:

    Ta có: y=fx=1x.

    Biểu thức 1x xác định khi x ≠ 0.

    Do đó tập xác định của hàm số đã cho: D = ℝ\0.

    a) Lấy hai giá trị x1, x2 tùy ý thuộc khoảng (0; + ∞) sao cho 0 < x1 < x2.

    Khi đó fx1=1x1 và fx2=1x2

    Vì  0 < x1 < x2  nên 1x1>1x2 hay f(x1) > f(x2).

    Vậy hàm số đã cho nghịch biến trên khoảng (0; + ∞).

    b) Lấy hai giá trị x1, x2 tùy ý thuộc khoảng (– ∞; 0) sao cho x1 < x2 < 0.

    Khi đó fx1=1x1 và fx2=1x2

    Vì x1 < x2 < 0 nên 1x1>1x2 hay f(x1) > f(x2).

    Vậy hàm số đã cho nghịch biến trên khoảng (– ∞; 0).

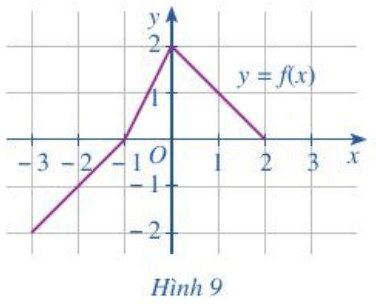
    Bài 7 trang 38 Toán lớp 10 Tập 1: Cho hàm số y = f(x) có đồ thị như Hình 9.

    Cho hàm số y = f(x) có đồ thị như Hình 9. Chỉ ra khoảng đồng biến

    Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).

    Lời giải:

    Quan sát đồ thị hàm số y = f(x) ở Hình 9, ta thấy:

    +) Trong khoảng (-3; 0) đồ thị hàm số đã cho “đi lên” nên hàm số đã cho đồng biến trên khoảng (-3; 0)

    +) Trong khoảng (0; 2) đồ thị hàm số đã cho “đi xuống” nên hàm số đã cho nghịch biến trên khoảng (0; 2).

    Vậy hàm số đã cho đồng biến trên khoảng (-3; 0) và nghịch biến trên khoảng (0; 2).

    Bài 8 trang 38 Toán lớp 10 Tập 1: Một lớp muốn thuê một chiếc xe khách cho chuyến tham quan với tổng đoạn đường cần di chuyển trong khoảng từ 550 km đến 600 km, có hai công ty được tiếp cận để tham khảo giá.

    Công ty A có giá khởi đầu là 3,75 triệu đồng cộng thêm 5 000 đồng cho mỗi ki-lô-mét chạy xe. 

    Công ty B có giá khởi đầu là 2,5 triệu đồng cộng thêm 7 500 đồng cho mỗi ki-lô-mét chạy xe. Lớp đó nên chọn công ty nào để chi phí là thấp nhất? 

    Lời giải:

    Đổi 3,75 triệu đồng = 3 750 000 đồng; 2,5 triệu đồng = 2 500 000 đồng.

    Gọi x (km) là tổng đoạn đường cần di chuyển của lớp (550 ≤ x ≤ 600) và y là chi phí lớp đó phải trả cho việc thuê xe.

    Ta có với mỗi giá trị của x có đúng một giá trị của y nên y là hàm số của x.

    Đối với công ty A, ta có số tiền cần trả được biểu diễn theo hàm số: 

    yA = 3 750 000 + 5000x

    Vì 550 ≤ x ≤ 600 nên 6 500 000 ≤ 3 750 000 + 5000x ≤ 6 750 000 hay 6 500 000 ≤  yA ≤ 6 750 000.

    Đối với công ty B, ta có số tiền cần trả được biểu diễn theo hàm số: 

    yB = 2 500 000 + 7500x

    Vì 550 ≤ x ≤ 600 nên 6 625 000 ≤ 2 500 000 + 7500x  ≤ 7 000 000 hay 6 625 000 ≤ yB ≤ 7 000 000.

    Ta thấy khoảng chi phí cho việc thuê xe của công ty A thấp hơn so với khoảng chi phí cho việc thuê xe ở công ty B với cùng số ki – lô – mét di chuyển.

    Vậy để chi phí là thấp nhất thì lớp đó nên chọn xe của công ty A.

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

    Giải Toán 10 trang 31 Tập 1

    Giải Toán 10 trang 32 Tập 1

    Giải Toán 10 trang 33 Tập 1

    Giải Toán 10 trang 34 Tập 1

    Giải Toán 10 trang 35 Tập 1

    Giải Toán 10 trang 36 Tập 1

    Giải Toán 10 trang 37 Tập 1

    Giải Toán 10 trang 38 Tập 1

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

    Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

    Bài 3: Dấu của tam thức bậc hai

    Bài 4: Bất phương trình bậc hai một ẩn

    Bài 5: Hai dạng phương trình quy về phương trình bậc hai

    Bài tập cuối chương 3

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 304 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: