Nội dung bài viết

    Xem thêm

    Giải SBT Toán 7 trang 74 Tập 1 Kết nối tri thức

    Với Giải SBT Toán 7 trang 74 Tập 1 trong Ôn tập chương 4 Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 74.

    1 350 30/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 7 trang 74 Tập 1 Kết nối tri thức

    Bài 4.58 trang 74 SBT Toán 7 Tập 1: Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P ∈ d, Q ∈ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:

    a) AP = BQ.

    b) ∆APB = ∆BQA.

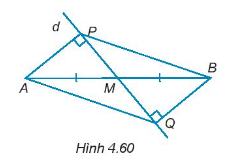
    Sách bài tập Toán 7 Ôn tập chương 4 - Kết nối tri thức (ảnh 1)

    Hướng dẫn giải

    a) Xét tam giác vuông PAM và tam giác vuông QBM có:

    AM = BM (do M là trung điểm của AB)

    PMA^=QMB^ (hai góc đối đỉnh)

    Do đó, ∆PAM = ∆QBM (cạnh huyền – góc nhọn).

    Suy ra AP = BQ.

    b) Xét tam giác APB và tam giác BQA có:

    AP = BQ (cmt)

    PAB^=QBA^ (do ∆PAM = ∆QBM)

    AB: cạnh chung

    Do đó, ∆APB = ∆BQA (c – g – c).

    Bài 4.59 trang 74 SBT Toán 7 Tập 1: Cho Hình 4.61, hãy tính số đo các góc của tam giác ABE.

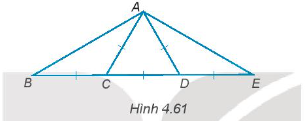
    Sách bài tập Toán 7 Ôn tập chương 4 - Kết nối tri thức (ảnh 1)

    Hướng dẫn giải

    Ta có: AD = AC = CD, do đó tam giác ACD là tam giác đều.

    Suy ra ACD^=ADC^=CAD^=60°.

    Ta có: ACB^+ACD^=180° (hai góc kề bù)

    ⇒ACB^=180°−ACD^=180°−60°=120°.

    Tam giác ABC có CB = CA nên tam giác ACB cân tại đỉnh C.

    Suy ra ABC^=BAC^.

    Ta có: A​BC^+BAC^+ACB^=180° (định lí tổng ba góc trong tam giác)

    Do đó, 2ABC^=180°−ACB^=180°−120°=60°.

    Suy ra ABC^=60°2=30°.

    Do đó, ABC^=BAC^=30°.

    Chứng minh tương tự đối với tam giác ADE cân tại đỉnh D, ta cũng có: DEA^=DAE^=30°

    Ta có:

    BAE^=BAC^+CAD^+DAE^=30°+60°+30°=120°.

    Vậy trong tam giác ABE có: ABE^=ABC^=30°; AEB^=DEA^=30° và BAE^=120°.

    Bài 4.60 trang 74 SBT Toán 7 Tập 1: Cho hình thang cân ABCD có đáy lớn AD và đáy nhỏ BC thỏa mãn AD = 4 cm và AB = BC = CD = 2 cm (H.4.62). Tính các góc của hình thang ABCD.

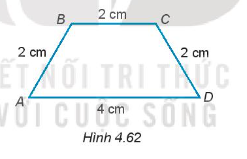
    Sách bài tập Toán 7 Ôn tập chương 4 - Kết nối tri thức (ảnh 1)

    Hướng dẫn giải

    Gọi O là trung điểm của AD.

    Khi đó, AO = OD = AD2=42=2 (cm).

    Do đó, AB = BC = CD = AO = OD = 2 cm.

    Tam giác ABO có AB = BO nên tam giác ABO cân tại đỉnh A.

    Suy ra ABO^=AOB^.

    Lại có: AD // BC (do ABCD là hình thang cân có AD và BC là đáy)

    Suy ra CBO^=AOB^ (hai góc so le trong).

    Do đó, ABO^=AOB^=CBO^.

    Xét tam giác ABO và tam giác CBO có:

    AB = BC (= 2 cm)

    ABO^=CBO^ (cmt)

    BO: cạnh chung

    Do đó, ∆ABO = ∆CBO (c – g – c).

    Suy ra CO = AO = 2 cm.

    Tam giác COD có CD = OD = OC (= 2 cm). Do đó tam giác COD là tam giác đều.

    Suy ra D^=CDO^=60°.

    Ta có: D^+BCD^=180° (BC // AD, hai góc ở vị trí trong cùng phía)

    Suy ra BCD​^=180°−D^=180°−60°=120°.

    Do ABCD là hình thang cân với AD và BC là đáy.

    Vậy A^=D^=60° và ABC^=BCD^=120°.

    Xem thêm lời giải sách bài tập Toán lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

    Giải SBT Toán 7 trang 71 Tập 1

    Giải SBT Toán 7 trang 72 Tập 1

    Giải SBT Toán 7 trang 73 Tập 1

    Xem thêm lời giải sách bài tập Toán lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

    Bài 12: Tổng các góc trong một tam giác

    Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

    Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

    Bài 15: Các trường hợp bằng nhau của tam giác vuông

    Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

    Xem thêm lời giải sách bài tập Toán lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

    Bài 12: Tổng các góc trong một tam giác

    Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

    Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

    Bài 15: Các trường hợp bằng nhau của tam giác vuông

    Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 350 30/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: