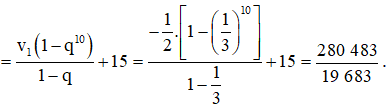Cho dãy số (un) biết u1 = 1, un = 1/3un-1 + 1 với n thuộc N*, n >= 2. Đặt vn = un - 3/2 với n thuộc N*
Lời giải Bài 44 trang 56 SBT Toán 11 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.
Giải SBT Toán 11 Bài 3: Cấp số nhân
Bài 44 trang 56 SBT Toán 11 Tập 1: Cho dãy số (un) biết u1 = 1, un=13un− 1+1 với n ∈ ℕ*, n ≥ 2. Đặt vn=un−32 với n ∈ ℕ*.
a) Chứng minh rằng dãy số (vn) là cấp số nhân. Tìm số hạng đầu, công bội của cấp số nhân đó.
b) Tìm công thức số hạng tổng quát của (vn), (un).
c) Tính tổng S = u1 + u2 + u3 + ... + u10.
Lời giải:
a) Ta có v1=u1−32=1−32=−12
vn=un−32=13un−1+1−32=13un−1−12=13(un−1−32)=13vn−1 với mọi n ∈ ℕ*, n ≥ 2.
Vậy dãy số (vn) là cấp số nhân với số hạng đầu v1=−12 và công bội q=13 .
b) Ta có: vn=v1.qn−1=−12.(13)n−1=−12.3n−1 .
Từ vn=un−32 , suy ra un=vn+32=32−12.3n−1=3.3n−1−12.3n−1=3n−12.3n−1 .
c) Ta có S = u1 + u2 + u3 + ... + u10
=(v1+32)+(v2+32)+(v3+32)+...+(v10+32)
= (v1 + v2 + v3 + ... + v10) + 32.10
Xem thêm Lời giải bài tập SBT Toán 11 sách Cánh diều hay, chi tiết khác:
Bài 30 trang 54 SBT Toán 11 Tập 1: Trong các dãy số sau, dãy số nào là cấp số nhân?
A. 128; – 64; 32; – 16; 8. B. √2; 2; 2√2; 4; 8 ...
Bài 31 trang 55 SBT Toán 11 Tập 1: Trong các dãy số (un) với số hạng tổng quát sau, dãy số nào là cấp số nhân? A. un = 5n. B. un = 1 + 5n. C. un = 5n + 1. D. un = 5 + n2...
Bài 34 trang 55 SBT Toán 11 Tập 1: Cho cấp số nhân (un), biết u2 . u6 = 64. Giá trị của u3 . u5 là A. – 8. B. – 64. C. 64. D. 8...
Bài 35 trang 55 SBT Toán 11 Tập 1: Cho (un) là cấp số nhân có u1=13 ; u8 = 729. Tổng 8 số hạng đầu của cấp số nhân đó là...
Bài 39 trang 55 SBT Toán 11 Tập 1: Tìm số hạng đầu và công bội của cấp số nhân (un), biết...
Bài 40 trang 55 SBT Toán 11 Tập 1: Cho (un) là cấp số nhân có u1 + u5 = 51 và u2 + u6 = 102.
a) Tính u10. b) Số 192 là số hạng thứ mấy của cấp số nhân trên...
Bài 43 trang 56 SBT Toán 11 Tập 1: Cho cấp số nhân (un) biết u1 = – 1, q = 3. a) Tính tổng 10 số hạng đầu của cấp số nhân đó...
Xem thêm Lời giải bài tập SBT Toán 11 sách Cánh diều hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều