Nội dung bài viết

    Xem thêm

    Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G, I, K lần lượt là trọng tâm các tam giác ABC, A'B'C'

    Lời giải Bài 43 trang 113 SBT Toán 11 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 1,454 18/09/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 11 Bài 5: Hình lăng trụ và hình hộp

    Bài 43 trang 113 SBT Toán 11: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G, I, K lần lượt là trọng tâm các tam giác ABC, A'B'C', A'B'B.

    a) Chứng minh rằng IK // (BCC'B').

    b) Chứng minh rằng (AGK) // (A'IC).

    c) Gọi (α) là mặt phẳng đi qua điểm K và song song với mặt phẳng (ABC). Mặt phẳng (α) cắt A'C tại điểm L. Tính LA'LC.

    Lời giải:

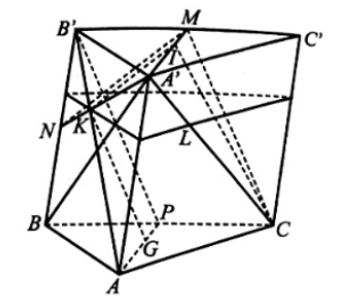
    Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G, I, K lần lượt là trọng tâm các tam giác ABC, A'B'C', A'B'B. a) Chứng minh rằng IK // (BCC'B'). b) Chứng minh rằng (AGK) // (A'IC). c) Gọi (α) là mặt phẳng đi qua điểm K và song song với mặt phẳng (ABC). Mặt phẳng (α) cắt A'C tại điểm L. Tính . (ảnh 1)

    a) Gọi M, N lần lượt là trung điểm của cạnh B'C', BB'.

    Do I, K lần lượt là trọng tâm của các tam giác A'B'C' và A'B'B nên A'IA'M=A'KA'N=23.

    Suy ra IK // MN. Mà MN ⊂ (BCC'B') nên IK // (BCC'B').

    b) Gọi P là trung điểm của cạnh BC.

    Khi đó, mặt phẳng (AGK) cũng là mặt phẳng (AB'P), mặt phẳng (A'IC) cũng là mặt phẳng (A'MC). 

    Ta có B'P // MC (B'MCP là hình bình hành) nên B'P // (A'MC)

    AP // A'M (APMA' là hình bình hành) nên AP // (A'MC).

    Từ đó, suy ra (AB'P) // (A'MC) hay (AGK) // (A'IC).

    c) Với K là trọng tâm của tam giác A'BB', ta suy ra B'KB'A=13 nên B'KKA=12.

    Ta có đường thẳng B'A cắt ba mặt phẳng song song (A'B'C'), (α), (ABC) lần lượt tại B', K, A; đường thẳng A'C cũng cắt ba mặt phẳng trên theo thứ tự tại A', L, C.

    Áp dụng định lí Thalés trong không gian, ta có: B'KA'L=KALC=AB'CA'.

    Suy ra A'LLC=B'KKA=12.

    Vậy LA'LC=12.

    Xem thêm Lời giải bài tập SBT Toán 11 sách Cánh diều hay, chi tiết khác:

    Bài 36 trang 112 SBT Toán 11: Số đường chéo trong một hình hộp là:...

    Bài 37 trang 112 SBT Toán 11: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của BC, B'C'....

    Bài 38 trang 112 SBT Toán 11: Cho hình hộp ABCD.A'B'C'D'. Khẳng định nào sau đây là sai?...

    Bài 39 trang 113 SBT Toán 11: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N lần lượt là trung điểm của A'B', B'C'....

    Bài 40 trang 113 SBT Toán 11: Cho hình hộp ABCD.A'B'C'D'. Mặt phẳng (BA'C') song song với mặt phẳng nào dưới đây?...

    Bài 41 trang 113 SBT Toán 11: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M là trung điểm của A'C'....

    Bài 42 trang 113 SBT Toán 11: Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P, Q, R, S lần lượt là trung điểm của...

    Bài 43 trang 113 SBT Toán 11: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi G, I, K lần lượt là trọng tâm các tam giác ABC, A'B'C', A'B'B....

    Bài 44 trang 113 SBT Toán 11: Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh.....

    Bài 45 trang 113 SBT Toán 11: Phần trong của một bể đựng nước được xây có dạng hình hộp như Hình 38....

    Xem thêm Lời giải bài tập SBT Toán 11 sách Cánh diều hay, chi tiết khác:

    Bài 2: Hai đường thẳng song song trong không gian

    Bài 3: Đường thẳng và mặt phẳng song song

    Bài 4: Hai mặt phẳng song song

    Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian

    Bài tập cuối chương 4

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,454 18/09/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: