Nội dung bài viết

    Xem thêm

    Cho hai đường thẳng song song a, b và một đường thẳng c (c cắt a tại E, c cắt b tại F). Hai tia phân giác của các góc aEF và bFE

    Lời giải Bài 83 trang 93 SBT Toán 7 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

    1 539 01/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 7 Cánh diều Bài 11. Tính chất ba đường phân giác của tam giác

    Bài 83 trang 93 SBT Toán 7 Tập 2: Cho hai đường thẳng song song a, b và một đường thẳng c (c cắt a tại E, c cắt b tại F). Hai tia phân giác của các góc aEF và bFE cắt nhau tại I. Gọi A, B lần lượt là hình chiếu của I trên các đường thẳng a và b (Hình 52). 

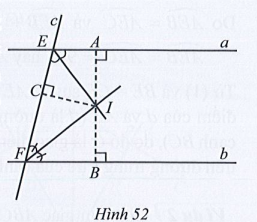
    Sách bài tập Toán 7 Bài 11 (Cánh diều): Tính chất ba đường phân giác của tam giác  (ảnh 1) 

    Chứng minh:

    a) Tam giác EIF là tam giác vuông;

    b) IA = IB.

    Lời giải

    a) Vì EI là tia phân giác của góc aEF nên AEI^=IEF^=12AEF^.

    Vì FI là tia phân giác của góc bFE nên BFI^=IFE^=12BFE^.

    Vì a // b nên aEF^+bFE^=180° (hai góc trong cùng phía)

    Suy ra IEF^+IFE^=aEF^+bFE^2=180°2=90°.

    Xét ∆IEF có IEF^+IFE^+EIF^=180° (tổng ba góc của một tam giác).

    Suy ra EIF^=180°−IEF^+IFE^=180°−90°=90°. 

    Vậy tam giác EIF là tam giác vuông tại I.

    b) Gọi C là hình chiếu của I trên đường thẳng c.

    Do EI là tia phân giác của góc AEF nên IA = IC (1)

    Do FI là tia phân giác của góc EFB nên IC = IB (2)

    Từ (1) và (2) ta có IA = IB.

    Vậy IA = IB.

    Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Bài 79 trang 92 SBT Toán 7 Tập 2: Cho tam giác ABC (AB < AC). Trên tia phân giác của góc A, lấy điểm E nằm trong tam giác ABC sao cho E cách đều hai cạnh AB, BC...

    Bài 80 trang 92 SBT Toán 7 Tập 2: Cho tam giác ABC có ABC^+ACB^=2BAC^. Hai tia phân giác của góc B và góc C cắt nhau tại K. Trong các phát biểu sau, phát biểu nào sai...

    Bài 81 trang 92 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A có K là trung điểm của đoạn BC. Hai đường phân giác BD và CE cắt nhau tại I...

    Bài 82 trang 92 SBT Toán 7 Tập 2: Cho tam giác ABC vuông tại C có CAB^=60°, AE là tia phân giác của góc CAB (E ∈ BC). Gọi D là hình chiếu của B trên tia AE...

    Bài 83 trang 93 SBT Toán 7 Tập 2: Cho hai đường thẳng song song a, b và một đường thẳng c (c cắt a tại E, c cắt b tại F). Hai tia phân giác của các góc aEF và bFE cắt nhau tại I...

    Bài 84* trang 93 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A có M là trung điểm của BC. G là giao điểm của hai trung tuyến BD và CE...

    Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Bài 10. Tính chất ba đường trung tuyến của tam giác

    Bài 11. Tính chất ba đường phân giác của tam giác

    Bài 12. Tính chất ba đường trung trực của tam giác

    Bài 13. Tính chất ba đường cao của tam giác

    Bài tập cuối chương 7

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 539 01/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: