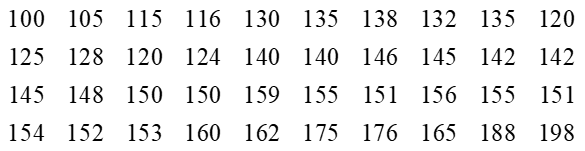Nội dung bài viết

    Xem thêm

    Bài 3 trang 25 Toán 11 Tập 2 | Cánh diều Giải Toán lớp 11

    Lời giải Bài 3 trang 25 Toán 11 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 318 09/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 11 Bài tập cuối chương 5 trang 25

    Bài 3 trang 25 Toán 11 Tập 2: Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong một tuần (đơn vị: kilômét) của 40 chiếc ô tô:

    Bài 3 trang 25 Toán 11 Tập 2 | Cánh diều Giải Toán 11

    a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy với năm nhóm ứng với năm nửa khoảng:

    [100; 120), [120; 140), [140; 160), [160; 180), [180; 200).

    b) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.

    c) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?

    Lời giải:

    a) Bảng tần số ghép nhóm bao gồm cả tần số tích lũy với năm nhóm ứng với năm nửa khoảng như sau:

    Nhóm

    Giá trị đại diện

    Tần số

    Tần số tích lũy

    [100; 120)

    [120; 140)

    [140; 160)

    [160; 180)

    [180; 200)

    110

    130

    150

    170

    190

    4

    10

    19

    5

    2

    4

    14

    33

    38

    40

    n = 40

    b) ⦁ Số trung bình cộng của mẫu số liệu ghép nhóm đã cho là:

    x¯=110⋅4+130⋅10+150⋅19+170⋅5+190⋅240 = 145,5.

    ⦁ Số phần tử của mẫu là n = 40. Ta có n2=402 = 20.

    Mà 14 < 20 < 33 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.

    Xét nhóm 3 là nhóm [140; 160) có r = 140, d = 20, n3 = 19 và nhóm 2 là nhóm [120; 140) có cf2 = 14.

    Áp dụng công thức, ta có trung vị của mẫu số liệu là:

    Me = 140+20−1419⋅20≈146,32 (km).

    Do đó tứ phân vị thứ hai là Q2 = Me ≈ 146,32 (km).

    ⦁ Ta có n4=404 = 10. Mà 4 < 10 < 14 nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.

    Xét nhóm 2 là nhóm [120; 140) có s = 120; h = 20; n2 = 10 và nhóm 1 là nhóm [100; 120) có cf1 = 4.

    Áp dụng công thức, ta có tứ phân vị thứ nhất là:

    Q1 = 20+10−410⋅20 = 132 (km).

    ⦁ Ta có 3n4=3⋅404 = 30. Mà 14 < 30 < 33 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.

    Xét nhóm 3 là nhóm [140; 160) có t = 140; l = 20; n3 = 19 và nhóm 2 là nhóm [120; 140) có cf2 = 14.

    Áp dụng công thức, ta có tứ phân vị thứ ba là:

    Q3 = 140+30−1419⋅20≈156,84 (km).

    c) Nhóm 3 là nhóm [140; 160) có tần số lớn nhất với u = 140, g = 20, n3 = 19 và nhóm 2 có tần số n2 = 10, nhóm 4 có tần số n4 = 5.

    Áp dụng công thức, ta có mốt của mẫu số liệu là:

    Mo = 140+19−102⋅19−10−5⋅20≈147,83 (km).

    Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác: 

    Bài 1 trang 25 Toán 11 Tập 2: Người ta tiến hành phỏng vấn 40 người về một mẫu áo sơ mi mới. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm 100...

    Bài 2 trang 25 Toán 11 Tập 2: Chọn ngẫu nhiên hai số khác nhau từ 21 số nguyên dương đầu tiên. Xác xuất để chọn được hai số có tổng là một số chẵn bằng...

    Bài 3 trang 25 Toán 11 Tập 2: Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong một tuần (đơn vị: kilômét) của 40 chiếc ô tô...

    Bài 4 trang 26 Toán 11 Tập 2: Bạn Dũng và bạn Hương tham gia đội văn nghệ của nhà trường. Nhà trường chọn từ đội văn nghệ đó một bạn nam và một bạn nữ để lập tiết mục song ca...

    Bài 5 trang 26 Toán 11 Tập 2: Hai bạn Mai và Thi cùng tham gia một kì kiểm tra ngoại ngữ một cách độc lập nhau. Xác suất để bạn Mai và bạn Thi đạt từ điểm 7 trở lên lần lượt là 0,8...

    Bài 6 trang 26 Toán 11 Tập 2: Một người chọn ngẫu nhiên 3 lá thư vào 3 phong bì đã ghi địa chỉ sao cho mỗi phong bì chỉ chứa một lá thư...

    Bài 7 trang 26 Toán 11 Tập 2: Một hộp chứa 9 quả cầu có cùng kích thước và khối lượng. Trong đó có 4 quả cầu màu xanh đánh số từ 1 đến 4...

    Bài 8 trang 26 Toán 11 Tập 2: Để nghiên cứu xác suất của một loại cây trồng mới phát triển bình thường, người ta trồng hạt giống của loại cây đó trên hai lô đất thí nghiệm A, B khác nhau...

    Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác: 

    Bài 2: Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất

    Bài 1: Phép tính lũy thừa với số mũ thực

    Bài 2: Phép tính lôgarit

    Bài 3: Hàm số mũ. Hàm số lôgarit

    Bài 4: Phương trình, bất phương trình mũ và lôgarit

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 318 09/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: