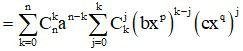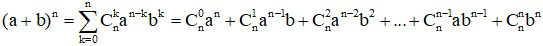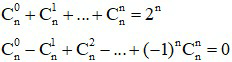Nội dung bài viết

    Xem thêm

    Xác định hệ số của x^3 trong khai triển biểu thức

    Lời giải Bài 34 trang 16 SBT Toán 10 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

    1 500 21/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 Cánh diều Bài 4: Nhị thức Newton

    Bài 34 trang 16 SBT Toán 10 Tập 2:

    Xác định hệ số của x3 trong khai triển biểu thức 23x+145 .

    Lời giải:

    Ta có: 23x+145=23x5+5.23x4.14+10.23x3.142+10.23x2.143

    +5.23x1.144+145=32243x5+2081x4+527x3+572x2+5384x+11024

    Số hạng chứa x3 trong khai triển biểu thức 23x+145 là 527x3 .

    Vậy hệ số của x3 trong khai triển biểu thức 23x+145 là 527 .

    *Phuơng pháp giải

    Dạng 1. Tìm số hàng chứa xm trong khai triển

    Phương pháp giải:

    * Với khai triển (axp + bxq)n (p, q là các hằng số)

    Ta có: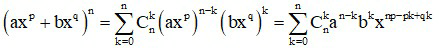Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11

    Số hạng chứa xm ứng với giá trị k thỏa mãn: np – pk + qk = m

    Từ đó tìm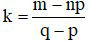Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11

    Vậy hệ số của số hạng chứa xm là: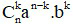Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11với giá trị k đã tìm được ở trên.

    * Với khai triển P(x) = (a + bxp + cxq)n (p, q là các hằng số)

    Ta có: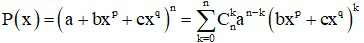Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11

    Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11

    Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của xm.

    * Chú ý:

    - Nếu k không nguyên hoặc k > n thì trong khai triển không chứa xm, hệ số phải tìm bằng 0.

    - Nếu hỏi hệ số không chứa x tức là tìm hệ số chứa x0.

    *Lý thuyết

    a) Định nghĩa:

    Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11

    b) Nhận xét:

    Trong khai triển Niu tơn (a + b)n có các tính chất sau

    - Gồm có n + 1 số hạng

    - Số mũ của a giảm từ n đến 0 và số mũ của b tăng từ 0 đến n

    - Tổng các số mũ của a và b trong mỗi số hạng bằng n

    - Các hệ số có tính đối xứng: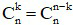Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11

    - Quan hệ giữa hai hệ số liên tiếp: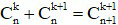Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11

    - Số hạng tổng quát thứ k + 1 của khai triển: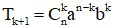Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11

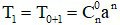
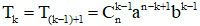
    Ví dụ: Số hạng thứ nhấtNhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11, số hạng thứ k:Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11

    c) Hệ quả:

    Ta có :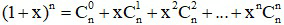Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11

    Từ khai triển này ta có các kết quả sau

    Nhị thức Niu tơn và cách giải các dạng bài tập hay, chi tiết | Toán lớp 11

    Xem thêm

    Lý thuyết Nhị thức Newton (công thức, khai triển) các dạng bài tập và cách giải

    TOP 40 câu Trắc nghiệm Nhị Thức Newton (có đáp án ) | Toán 11

    Xem thêm các bài giải sách giáo khoa Toán 10 bộ sách Cánh diều hay, chi tiết khác:

    Bài 28 trang 15 SBT Toán 10 Tập 2:Trong các phát biểu sau, phát biểu nào sai?...

    Bài 29 trang 16 SBT Toán 10 Tập 2:Trong các phát biểu sau, phát biểu nào đúng?...

    Bài 30 trang 16 SBT Toán 10 Tập 2:Hệ số của x3 trong khai triển biểu thức (2x – 1)4 là:...

    Bài 31 trang 16 SBT Toán 10 Tập 2:Hệ số của x trong khai triển biểu thức (x – 2)5 là:...

    Bài 32 trang 16 SBT Toán 10 Tập 2:Khai triển các biểu thức sau:...

    Bài 33 trang 16 SBT Toán 10 Tập 2:Xác định hệ số của x2 trong khai triển biểu thức (4x – 3)4....

    Bài 34 trang 16 SBT Toán 10 Tập 2:Xác định hệ số của x3 trong khai triển biểu thức...

    Bài 35 trang 16 SBT Toán 10 Tập 2:Cho 2x−134=a0+a1x+a2x2+a3x3+a4x4 . Tính:...

    Bài 36 trang 16 SBT Toán 10 Tập 2:Cho 35x+125=a0+a1x+a2x2+a3x3+a4x4+a5x5 . Tính:...

    Bài 37* trang 16 SBT Toán 10 Tập 2:Tính các tổng sau (không sử dụng máy tính cầm tay):...

    Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều với cuộc sống hay, chi tiết khác: 

    Bài ôn tập chương 4

    Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây

    Bài 2: Hoán vị. Chỉnh hợp

    Bài 3: Tổ hợp

    Bài tập cuối chương V

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 500 21/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: