TOP 40 câu hỏi Trắc nghiệm Ôn tập chương 1 (Cánh diều 2024) có đáp án - Toán 6
Bộ 40 câu hỏi trắc nghiệm Toán lớp 6 Ôn tập chương 1 có đáp án đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 6 Chương 1.
Trắc nghiệm Toán 6 Ôn tập chương 1 – Cánh diều
Câu 1: Các viết tập hợp nào sau đây đúng?
A. A = [1; 2; 3; 4]
B. A = (1; 2; 3; 4)
C. A = {1, 2, 3, 4}
D. A = {1; 2; 3; 4}
Đáp án: D
Giải thích:
Các phần tử của tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu “:”.
Nên cách viết đúng là A = {1; 2; 3; 4}.
Câu 2: Cho các cách viết sau: A = {a, b, c, d}; B = {2; 13; 45}; C = (1; 2; 3); D = 1. Có bao nhiêu cách viết tập hợp là đúng trong các cách viết trên?
A. 1
B. 2
C. 3
D. 4
Đáp án: A
Giải thích:
Các phần tử của tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu “:”.
Nên cách viết đúng là B = {2; 13; 45}
Vậy có 1 cách viết đúng.
Câu 3: Viết tập hợp P các chữ cái tiếng Việt trong cụm từ: “HỌC SINH”.
A. P = {H; O; C; S; I; N; H}
B. P = {H; O; C; S; I; N}
C. P = {H; C; S; I; N}
D. P = {H; O; C; H; I; N}
Đáp án: B
Giải thích:
Các chữ cái tiếng Việt trong cụm từ “HỌC SINH” lần lượt là: H; O; C; S; I; N; H.
Mà trong tập hợp, mỗi phần tử ta chỉ liệt kê một lần, nên ta thấy trong từ “HỌC SINH” có hai chữ cái H, vậy khi viết tập hợp ta chỉ cần liệt kê một lần.
Do đó ta viết: P = {H; O; C; S; I; N}.
Câu 4: Cho hình vẽ
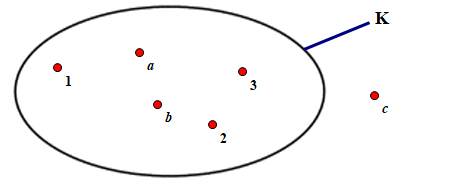
Tập hợp K là:
A. K = {1; 2; 3; a; b; c}
B. K = {1, 2, 3, a, b, c}
C. K = {1; 2; 3; a; b}
D. K = {1, 2, 3, a, b}
Đáp án: C
Giải thích:
Quan sát hình vẽ ta thấy các phần tử 1; 2; 3; a; b nằm trong vòng kín biểu diễn tập hợp K, nên các phần tử này thuộc tập hợp K, hơn nữa ta biểu diễn các phần tử trong tập hợp ngăn cách nhau bởi dấu “;”, do đó ta viết tập hợp K là:
K = {1; 2; 3; a; b}.
Câu 5: Trường hợp nào sau đây chỉ tập hợp số tự nhiên?
A. {1; 2; 3; 4; …}
B. {0; 1; 2; 3; 4; …}
C. {0; 1; 2; 3; 4; …}
D. {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
Đáp án: B
Giải thích:
Các số 0, 1, 2, 3, 4 … là các số tự nhiên.
Tập hợp các số tự nhiên được kí hiệu là , tức là = {0; 1; 2; 3; 4; …}.
Câu 6: Các số La Mã XV, XXI được đọc lần lượt là:
A. mười lăm, hai mốt
B. mười năm, hai mốt
C. mười lăm, hai mươi mốt
D. mười bốn, mười chín
Đáp án: C
Giải thích:
Câu 7: Điền tiếp hai số tự nhiên vào dãy số sau để được dãy ba số tự nhiên liên tiếp giảm dần:
1 256 ; …; …
A. 1 257 và 1 258
B. 1 258 và 1 260
C. 1 255 và 1 253
D. 1 255 và 1 254
Lời giả
Đáp án: D
Giải thích:
i
Vì đây là dãy số tự nhiên liên tiếp giảm dần nên:
Số thứ hai là: 1 256 – 1 = 1 255
Số thứ ba là: 1 255 – 1 = 1 254
Vậy hai số cần điền là 1 255 và 1 254.
Câu 8: Cho hai số tự nhiên 99; 100. Hãy tìm số tự nhiên a để ba số đó lập thành ba số tự nhiên liên tiếp?
A. 98
B. 97
C. 101
D. Cả A và C
Đáp án: D
Giải thích:
Số liền trước số 99 là số 98 nên có ba số tự nhiên liên tiếp là 98; 99; 100.
Số liền sau số 100 là số 101 nên có ba số tự nhiên liên tiếp là 99; 100; 101.
Câu 9: Tìm chữ số thích hợp ở dấu * sao cho: .
A. 2
B. 3
C. 4
D. Cả A và B
Đáp án: D
Giải thích:
Vì * là chữ số hàng chục của số nên * nhận là các số tự nhiên từ 0 đến 9.
Lại có:
Mà số 2 021, , 2 041 đều có các chữ số hàng nghìn, hàng trăm và hàng đơn vị là giống nhau. Do đó * thỏa mãn:
Hay * là các số tự nhiên lớn hơn hoặc bằng 2 và nhỏ hơn 4, đó là 2 và 3.
Vậy đáp án A và B đều đúng.
Câu 10: Tính nhanh tổng 53 + 25 + 47 + 75?
A. 200
B. 201
C. 300
D. 100
Đáp án: A
Giải thích:
Ta có: 53 + 25 + 47 + 75 = (53 + 47) + (25 + 75)
= 100 + 100 = 200
Câu 11: Kết quả của phép tính 418 – 18 – 100 là:
A. 200
B. 300
C. 400
D. 100
Đáp án: B
Giải thích:
Câu 12: Hiệu của số 12 300 và 1 200 là:
A. 11 100
B. 11 111
C. 1 100
D. 12 100
Đáp án: A
Giải thích:
Hiệu của 12 300 và 1 200 là kết quả của phép tính: 12 300 – 1 200.
Ta đặt tính rồi tính như sau:
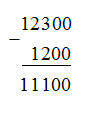
Vậy 12 300 – 1 200 = 11 110.
Chọn đáp án A.
Câu 13: Tìm số tự nhiên x, biết: x – 124 = 567.
A. x = 691
B. x = 443
C. x = 961
D. x = 434
Đáp án: A
Giải thích:
Ta có: x – 124 = 567
x = 567 + 124
x = 691
Vậy x = 691.
Câu 14: Kết quả của tổng 1 + 3 + 5 + 7 + 9 + … + 19 có chữ số tận cùng là:
A. 9
B. 7
C. 5
D. 0
Đáp án: D
Giải thích:
Ta có: 1 + 3 + 5 + 7 + 9 + … + 19
= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
= (1 + 19) + (3 + 17) + (5 + 15) + (7 + 13) + (9 + 11)
= 20 + 20 + 20 + 20 + 20
= 40 + 20 + 20 + 20
= 60 + 20 + 20
= 80 + 20 = 100
Vậy kết quả của tổng 1 + 3 + 5 + 7 + 9 + … + 19 có chữ số tận cùng là 0.
Câu 15: Kết quả của phép tính 25 . 12 . 4 là:
A. 1 000
B. 1 200
C. 120
D. 12 000
Đáp án: B
Giải thích:
Câu 16: Phép chia a : b thực hiện được khi:
A. b là số tự nhiên bất kì
B. b = 0
C. b ≠ 0
D. b ≠ 1
Đáp án: C
Giải thích:
Câu 17: Số tự nhiên x nào dưới đây thỏa mãn: 2 021 . (x – 2 021) = 2 021.
A. 2 020
B. 2 021
C. 2 022
D. 2 023
Đáp án: C
Giải thích:
Ta có: 2 021 . (x – 2 021) = 2 021
x – 2 021 = 2 021 : 2 021
x – 2 021 = 1
x = 1 + 2 021
x = 2 022
Vậy x = 2 022.
Câu 18: Chọn đáp án sai.
A. 53 < 35
B. 34 > 25
C. 43 = 26
D. 43 > 82
Đáp án: D
Giải thích:
Ta có:
+) 53 = 125; 35 = 243 suy ra 53 < 35 nên A đúng.
+) 34 = 81; 25 = 32 suy ra 34 > 25 nên B đúng.
+) 43 = 64; 26 = 64 suy ra 43 = 26 nên C đúng.
+) 43 = 64; 82 = 64 suy ra 43 = 82 nên D sai.
Câu 19: Tìm số tự nhiên n thỏa mãn 3n = 81.
A. n = 2
B. n = 3
C. n = 4
D. n = 8
Đáp án: C
Giải thích:
Câu 20: Tìm số tự nhiên n thỏa mãn 4n = 43 . 45?
A. n = 32
B. n = 16
C. n = 8
D. n = 4
Đáp án: C
Giải thích:
Câu 21: Tìm số tự nhiên m thỏa mãn 202018 < 20m < 202020 ?
A. m = 2 020
B. m = 2 019
C. m = 2 018
D. m = 20
Đáp án: B
Giải thích:
Ta có: 202018 < 20m < 202020
Suy ra: 2 018 < m < 2 020
Mà m là số tự nhiên nên m = 2 019.
Vậy m = 2 019.
Câu 22: Giá trị của biểu thức 2 . [(195 + 35 : 7) : 8 + 195] – 400 bằng
A. 140
B. 60
C. 80
D. 40
Đáp án: D
Giải thích:
Ta có: 2 . [(195 + 35 : 7) : 8 + 195] – 400
= 2 . [(195 + 5) : 8 + 195] – 400
= 2 . [200 : 8 + 195] – 400
= 2 . [25 + 195] – 400
= 2 . 220 – 400 = 40
Câu 23: Kết quả của phép tính 34 . 6 – [131 – (15 – 9)2] là:
A. 319
B. 931
C. 193
D. 391
Đáp án: D
Giải thích:
Ta có: 34 . 6 – [131 – (15 – 9)2]
= 34 . 6 – [131 – 62]
= 81 . 6 – [131 – 36]
= 81 . 6 – 95
= 486 – 95 = 391
Câu 24: Nếu x 2 và y 4 thì tổng x + y chia hết cho?
A. 2
B. 4
C. 8
D. Không xác định
Đáp án: A
Giải thích:
Ta có: y 4 nên suy ra y 2 (vì 4 chia hết cho 2)
Khi đó ta có:
x 2 và y 2 nên suy ra (x + y) 2 (theo tính chất chia hết của một tổng).
Câu 25: Viết tập hợp A tất cả các bội của 3 trong các số sau: 4; 18; 75; 124; 185; 258.
A. A = {4; 75; 124}
B. A = {18; 124; 258}
C. A = {75; 124; 258}
D. A = {18; 75; 258}
Đáp án: D
Giải thích:
Trong các số đã cho, ta thấy: 18 : 3 = 6, 75 : 3 = 25, 258 : 3 = 86.
Do đó ta có: 18 3, 75 3, 258 3 nên 18; 75; 258 là các bội của 3.
Vậy ta viết tập hợp A là: A = {18; 75; 258}.
Câu 26: Tập hợp các số tự nhiên x thỏa mãn 6 (x – 2) là:
A. {1; 2; 3; 6}
B. {3; 6}
C. {5; 8}
D. {3; 4; 5; 8}
Đáp án: D
Giải thích:
Vì 6 (x – 2) nên x – 2 là ước của 6.
Mà các ước của 6 là: 1, 2, 3, 6.
Nên ta có các trường hợp sau:
• TH1: x – 2 = 1
Suy ra x = 1 + 2 = 3 (t/m)
• TH2: x – 2 = 2
Suy ra x = 2 + 2 = 4 (t/m)
• TH3: x – 2 = 3
Suy ra x = 3 + 2 = 5 (t/m)
• TH4: x – 2 = 6
Suy ra x = 6 + 2 = 8 (t/m)
Vậy tập hợp các số tự nhiên x thỏa mãn yêu cầu bài toán là: {3; 4; 5; 8}.
Câu 27: Tổng (hiệu) nào dưới đây chia hết cho 5?
A. 136 + 420
B. 621 – 450
C. 1 . 2 . 3 . 4 . 5 + 42
D. 1 . 2 . 3 . 4 . 5 . 6 – 35
Đáp án: D
Giải thích:
Vì 5 chia hết cho 5 nên theo tính chất chia hết của một tích ta có
1 . 2 . 3 . 4 . 5 . 6 chia hết cho 5
Lại có 35 có chữ số tận cùng là 5 nên 35 chia hết cho 5
Do đó theo tính chất chia hết của một hiệu ta có
1 . 2 . 3 . 4 . 5 . 6 – 35 chia hết cho 5.
Câu 28: Tìm số thích hợp ở dấu * để số chia hết cho 9.
A. * = 1
B. * = 3
C. * = 8
D. * = 9
Đáp án: C
Giải thích:
Số có tổng các chữ số là 3 + * + 7 = 10 + *
Ta có chia hết cho 9 thì 10 + * cũng phải chia hết cho 9
Trong các đáp án đã cho, ta thấy chỉ có * = 8 là thỏa mãn (vì 10 + 8 = 18 chia hết cho 9).
Vậy * = 8.
Câu 29: Tìm các số tự nhiên x, y biết rằng chia hết cho 2, 5 và 9.
A. x = 0; y = 6
B. x = 6; y = 0
C. x = 8; y = 0
D. x = 0; y = 8
Đáp án: C
Giải thích:
Ta có x, y là các chữ số trong số nên x, y ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}
Theo giả thiết ta có chia hết cho 2 và 5 nên y = 0, ta được số
Mà nên 2 + 3 + x + 5 chia hết cho 9 hay (10 + x) chia hết cho 9.
Thử các kết quả ta thấy x = 8 thỏa mãn yêu cầu bài.
Vậy x = 8; y = 0.
Câu 30: Kết quả của phép tính nào sau đây là số nguyên tố.
A. 15 – 5 + 3
B. 7 . 2 + 1
C. 14 . 6 : 4
D. 6 . 4 – 12 . 2
Đáp án: A
Giải thích:
Ta có
+ Đáp án A: 15 – 5 + 3 = 13 là số nguyên tố.
+ Đáp án B: 7 . 2 + 1 = 15 là hợp số.
+ Đáp án C: 14 . 6 : 4 = 84 : 4 = 21 là hợp số.
+ Đáp án D: 6 . 4 – 12 . 2 = 24 – 24 = 0 không phải là số nguyên tố, cũng không phải là hợp số.
Câu 31: Cho các số 21; 71; 77; 101. Chọn phát biểu đúng trong các phát biểu sau?
A. Số 21 là hợp số, các số còn lại là số nguyên tố
B. Có hai số nguyên tố và hai số là hợp số trong các số trên
C. Chỉ có một số nguyên tố, còn lại là hợp số
D. Không có số nguyên tố nào trong các số trên
Đáp án: B
Giải thích:
+ Số 21 có các ước là 1; 3; 7; 21 nên 21 là hợp số.
+ Số 71 chỉ có hai ước là 1; 71 nên 71 là số nguyên tố.
+ Số 77 có các ước là 1; 7; 11; 77 nên 77 là hợp số.
+ Số 101 chỉ có hai ước là 1; 101 nên 101 là số nguyên tố.
Vậy trong các số đã cho, có 2 số là số nguyên tố và hai số là hợp số.
Câu 32: Số tự nhiên a lớn nhất thỏa mãn 90 a và 135 a là:
A. 15
B. 30
C. 45
D. 60
Đáp án: C
Giải thích:
Vì 90 a nên a là ước của 90
và 135 a nên a là ước của 135
Suy ra a là ước chung của 90 và 135.
Vì a là số lớn nhất thỏa mãn điều kiện trên nên a = ƯCLN (90, 135).
Phân tích các số 90 và 135 ra thừa số nguyên tố, ta được:
90 = 2 . 32 . 5
135 = 33 . 5
Vậy ƯCLN(90, 135) = 32 . 5 = 45 hay a = 45.
Câu 33: Trong hai số sau, hai số nào là hai số nguyên tố cùng nhau:
A. 2 và 6
B. 3 và 10
C. 6 và 9
D. 15 và 33
Đáp án: B
Giải thích:
Ta có:
ƯC(2, 6) = {1; 2} nên ƯCLN(2, 6) = 2
ƯC(3, 10) = {1} nên ƯCLN(3, 10) = 1
ƯC(6, 9) = {1; 3} nên ƯCLN(6, 9) = 3
ƯC(15, 33) = {1; 3} nên ƯCLN(15, 33) = 3
Chú ý: Hai số gọi là nguyên tố cùng nhau nếu chúng có ước chung lớn nhất là 1.
Vậy 3 và 10 là hai số nguyên tố cùng nhau.
Câu 34: BCNN(40, 28, 140) là:
A. 140
B. 280
C. 420
D. 560
Đáp án: B
Giải thích:
Ta có:
40 = 23 . 5
28 = 22 . 7
140 = 22 . 5 . 7
Do đó: BCNN(40, 28, 140) = 23 . 5 . 7 = 280.
Câu 35: Học sinh lớp 6A khi xếp hàng 2, hàng 3, hàng 6, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng từ 40 đến 60. Số học sinh của lớp 6A là:
A. 48
B. 54
C. 60
D. 72
Đáp án: A
Giải thích:
Gọi x là số học sinh lớp 6A, .
Vì khi xếp hàng 2, hàng 3, hàng 6, hàng 8 đều vừa đủ hàng nên
x 2, x 3, x 6, x 8
Do đó x là bội chung của 2; 3; 6 và 8.
Ta có:
6 = 2 . 3
8 = 23
Do đó: BCNN(2, 3, 6, 8) = 23 . 3 = 24
Suy ra BC(2, 3, 6, 8) = B(24) = {0; 24; 48; 72; ...}
Vì 40 < x < 60
Do đó: x = 48.
Các câu hỏi trắc nghiệm Toán lớp 6 sách Cánh diều có đáp án, chọn lọc khác:
Trắc nghiệm Bài 1: Số nguyên âm
Trắc nghiệm Bài 2: Tập hợp các số nguyên
Trắc nghiệm Bài 3: Phép cộng các số nguyên
Xem thêm các chương trình khác:
- Trắc nghiệm Địa Lí lớp 6 có đáp án – Kết nối tri thức
- Trắc nghiệm Toán lớp 6 có đáp án – Kết nối tri thức
- Trắc nghiệm Công nghệ lớp 6 có đáp án – Kết nối tri thức
- Trắc nghiệm GDCD lớp 6 có đáp án – Kết nối tri thức
- Trắc nghiệm Khoa học tự nhiên lớp 6 có đáp án – Kết nối tri thức
- Trắc nghiệm Văn lớp 6 có đáp án – Kết nối tri thức
- Trắc nghiệm Tiếng Anh lớp 6 có đáp án – Kết nối tri thức
- Trắc nghiệm Lịch sử lớp 6 có đáp án - Kết nối tri thức
- Trắc nghiệm Tin học lớp 6 có đáp án – Kết nối tri thức
- Trắc nghiệm Địa Lí lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Khoa học tự nhiên lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Toán lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Văn lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 6 có đáp án – Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh 6 Right on có đáp án
- Trắc nghiệm Tiếng Anh 6 English Discovery có đáp án
- Trắc nghiệm Tiếng Anh 6 iLearn Smart World có đáp án
