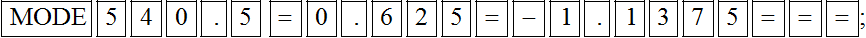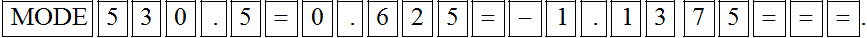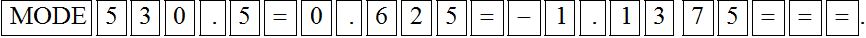Lý thuyết Phương trình bậc hai một ẩn Toán 9 (Kết nối tri thức)

Lý thuyết Toán 9 Bài 19: Phương trình bậc hai một ẩn

1. Định nghĩa phương trình bậc hai một ẩn

Nhận biết phương trình bậc hai một ẩn

Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng

ax² + bx + c = 0,

trong đó x là ẩn; a, b, c là những số cho trước gọi là hệ số và a ≠ 0.

Ví dụ 1. Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn? Chỉ rõ các hệ số a, b, c của mỗi phương trình bậc hai một ẩn đó.

a) 0x² – 8 = 0;

b) $-4y^2+12y+\frac{2}{7}=0;$

c) $12t^2+\sqrt{3}=0;$

d) –x² + (2m + 5)x – 10 = 0;

e) x⁴ + 2x² – 6 = 0.

Hướng dẫn giải

a) Phương trình 0x² – 8 = 0 không là phương trình bậc hai một ẩn vì hệ số a = 0.

b) Phương trình $-4y^2+12y+\frac{2}{7}=0$ là phương trình bậc hai ẩn y và có các hệ số $a=-4,b=12,c=\frac{2}{7}.$

c) Phương trình $12t^2+\sqrt{3}=0$ là phương trình bậc hai ẩn t và có các hệ số $a=12;b=0;c=\sqrt{3}.$

d) Phương trình –x² + (2m + 5)x – 10 = 0 là phương trình bậc hai ẩn x và có các hệ số a = –1; b = 2m + 5; c = –10.

e) Phương trình x⁴ + 2x² – 6 = 0 không là phương trình bậc hai một ẩn vì phương trình này có chứa x⁴.

2. Cách giải phương trình bậc hai một ẩn có dạng đặc biệt

Cách giải phương trình bậc hai một ẩn dạng khuyết

– Giải một phương trình bậc hai là tìm tất cả các nghiệm của nó.

– Ta giải một số phương trình bậc hai dạng ax² + bx + c = 0 (a ≠ 0), mà khuyết số hạng bậc nhất (tức là b = 0) hoặc khuyết số hạng tự do (tức là c = 0) bằng phương pháp đặt nhân tử chung đưa về dạng tích hoặc dùng hằng đẳng thức để đưa vế trái về một bình phương.

Chú ý:

⦁ Nếu A.B = 0 thì A = 0 hoặc B = 0;

⦁ Nếu A² = B (B ≥ 0) thì $A=\sqrt{B}$ hoặc $A=-\sqrt{B}.$

Ví dụ 2. Giải các phương trình:

a) 3x² + 9x = 0;

b) x² – 16 = 0;

c) (x – 1)² = 4.

Hướng dẫn giải

a) 3x² + 9x = 0

  3x(x + 3) = 0

  x = 0 hoặc x + 3 = 0

  x = 0 hoặc x = –3.

Vậy phương trình có hai nghiệm là: x₁ = 0, x₂ = –3.

b) x² – 16 = 0

  x² = 16

  x = 4 hoặc x = –4.

Vậy phương trình có hai nghiệm là: x = 4, x = –4.

c) (x – 1)² = 4

  x – 1 = 2 hoặc x – 1 = –2

  x = 3 hoặc x = –1.

Vậy phương trình có hai nghiệm là: x = 3, x = –1.

Chú ý: Để giải phương trình bậc hai dạng x² + bx = c, ta có thể cộng thêm vào hai vế của phương trình với cùng một số thích hợp để vế trái có thể biến đổi thành một bình phương. Từ đó có thể giải phương trình đã cho.

Ví dụ 3. Giải phương trình x² – 10x + 5 = 29.

Hướng dẫn giải

Ta có:

x² – 10x + 5 = 29

x² – 10x + 5 + 20 = 29 + 20

x² – 10x + 25 = 49

(x – 5)² = 49

x – 5 = 7 hoặc x – 5 = –7

x = 12 hoặc x = –2.

Vậy phương trình có hai nghiệm là: x = 12, x = –2.

3. Công thức nghiệm của phương trình bậc hai

3.1. Cách giải phương trình bậc hai

Để giải phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) trong trường hợp tổng quát, ta làm như sau:

– Chuyển hạng tử tự do c sang vế phải: ax² + bx = –c.

– Chia cả hai vế của phương trình cho hệ số a của x²: $x^2+\frac{b}{a}x=-\frac{c}{a}.$

– Cộng vào hai vế của phương trình nhận được với $\frac{b^2}{4a^2}$ để vế trái có thể biến đổi thành bình phương của một biểu thức: $x^2+\frac{b}{a}x+\frac{b^2}{4a^2}=-\frac{c}{a}+\frac{b^2}{4a^2}$ hay ${\left(x+\frac{b}{2a}\right)}^2=\frac{b^2-4ac}{4a^2}.$

Kí hiệu ∆ = b² – 4ac và gọi là biệt thức của phương trình (∆ đọc là “đenta”). Khi đó, ta có thể viết lại phương trình cuối dưới dạng ${\left(x+\frac{b}{2a}\right)}^2=\frac{\Delta }{4a^2}.$

3.2. Công thức nghiệm của của phương trình bậc hai

Xét phương trình bậc hai một ẩn ax² + bx + c = 0 (a ≠ 0).

Tính biệt thức ∆ = b² – 4ac.

⦁ Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a};x_2=\frac{-b-\sqrt{\Delta }}{2a}.$

⦁ Nếu ∆ = 0 thì phương trình có nghiệm kép $x_1=x_2=-\frac{b}{2a}.$

⦁ Nếu ∆ < 0 thì phương trình vô nghiệm.

Ví dụ 4. Áp dụng công thức nghiệm, giải các phương trình sau:

a) x² – 7x + 12 = 0;

b) –x² + 16x – 64 = 0;

c) 4x² + 3x + 10 = 0.

Hướng dẫn giải

a) Ta có: ∆ = b² – 4ac = (–7)² – 4.1.12 = 1 > 0 và $\sqrt{\Delta }=\sqrt{1}=1.$

Do đó, phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-\left(-7\right)+1}{2\cdot 1}=4;$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-\left(-7\right)-1}{2\cdot 1}=3.$

Vậy phương trình có hai nghiệm phân biệt là x₁ = 4, x₂ = 3.

b) Ta có: ∆ = b² – 4ac = 16² – 4.(–1).(–64) = 0.

Do đó, phương trình có nghiệm kép:

$x_1=x_2=-\frac{b}{2a}=-\frac{16}{2\cdot \left(-1\right)}=8.$

Vậy phương trình có nghiệm kép x₁ = x₂ = 8.

c) Ta có: ∆ = b² – 4ac = 3² – 4.4.10 = –151 < 0.

Vậy phương trình vô nghiệm.

3.3. Công thức nghiệm thu gọn của phương trình bậc hai

Xét phương trình bậc hai ax² + bx + c = 0 (a ≠ 0), với b = 2b’ và ∆’ = b’² – ac.

⦁ Nếu ∆’ > 0 thì phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b^{\text{'}}+\sqrt{{\Delta }^{\text{'}}}}{a};x_2=\frac{-b^{\text{'}}-\sqrt{{\Delta }^{\text{'}}}}{a}.$

⦁ Nếu ∆’ = 0 thì phương trình có nghiệm kép $x_1=x_2=-\frac{b^{\text{'}}}{a}.$

⦁ Nếu ∆’ < 0 thì phương trình vô nghiệm.

Ví dụ 5. Xác định a, b’, c và sử dụng công thức nghiệm thu gọn để giải các phương trình sau:

a) –4x² + 2x + 5 = 0;

b) $\sqrt{5}{x}^2+20x+20\sqrt{5}=0;$

c) x² – 4x + 9 = 0.

Hướng dẫn giải

a) Ta có: a = –4, b’ = 1, c = 5 và ∆’ = b’² – ac = 1² – (–4).5 = 21 > 0.

Do đó, phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b^{\text{'}}+\sqrt{{\Delta }^{\text{'}}}}{a}=\frac{-1+\sqrt{21}}{-4}=\frac{1-\sqrt{21}}{4};$

$x_2=\frac{-b^{\text{'}}-\sqrt{{\Delta }^{\text{'}}}}{a}=\frac{-1-\sqrt{21}}{-4}=\frac{1+\sqrt{21}}{4}.$

Vậy phương trình có hai nghiệm phân biệt là: $x_1=\frac{1-\sqrt{21}}{4};x_2=\frac{1+\sqrt{21}}{4}.$

b) Ta có: $a=\sqrt{5},b^{\text{'}}=10,c=20\sqrt{5}$ và ${\Delta }^{\text{'}}={b^{\text{'}}}^2-ac={10}^2-\sqrt{5}\cdot 20\sqrt{5}=0.$

Do đó, phương trình có nghiệm kép: $x_1=x_2=-\frac{b^{\text{'}}}{a}=-\frac{10}{\sqrt{5}}=-2\sqrt{5}.$

Vậy phương trình có nghiệm kép là: $x_1=x_2=-2\sqrt{5}.$

c) Ta có: a = 1, b’ = –2, c = 9 và ∆’ = b’² – ac = (–2)² – 1.9 = –5 < 0.

Vậy phương trình vô nghiệm.

4. Tìm nghiệm của phương trình bậc hai bằng máy tính cầm tay

Sử dụng máy tính cầm tay, ta có thể dễ dàng tìm nghiệm của các phương trình bậc hai một ẩn.

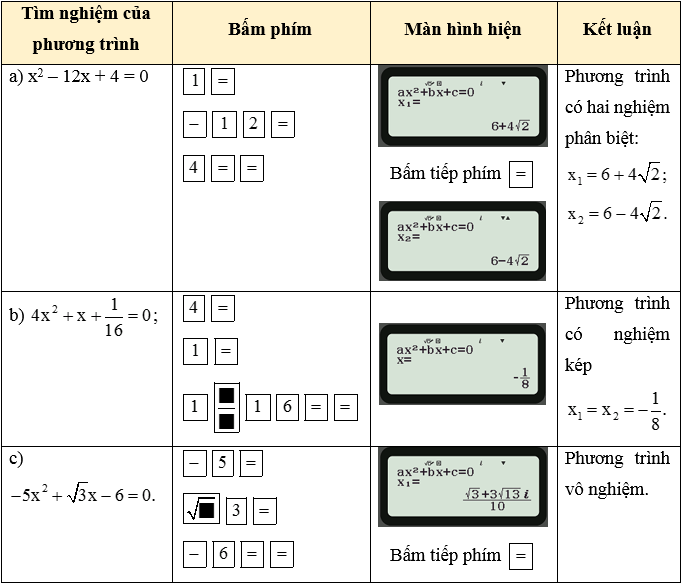
Ví dụ 6. Sử dụng máy tính cầm tay, tìm nghiệm của các phương trình sau:

a) x² – 12x + 4 = 0;

b) $4x^2+x+\frac{1}{16}=0;$

c) $-5x^2+\sqrt{3}x-6=0.$

Hướng dẫn giải

Với một loại máy tính cầm tay, sau khi mở máy ta bấm phím để chuyển về chế độ giải phương trình bậc hai.

Tiếp theo, với từng phương trình, ta thực hiện như sau:

Chú ý: Để hiển thị kết quả xấp xỉ ở dạng số thập phân sau khi nhận kết quả ta bấm phím

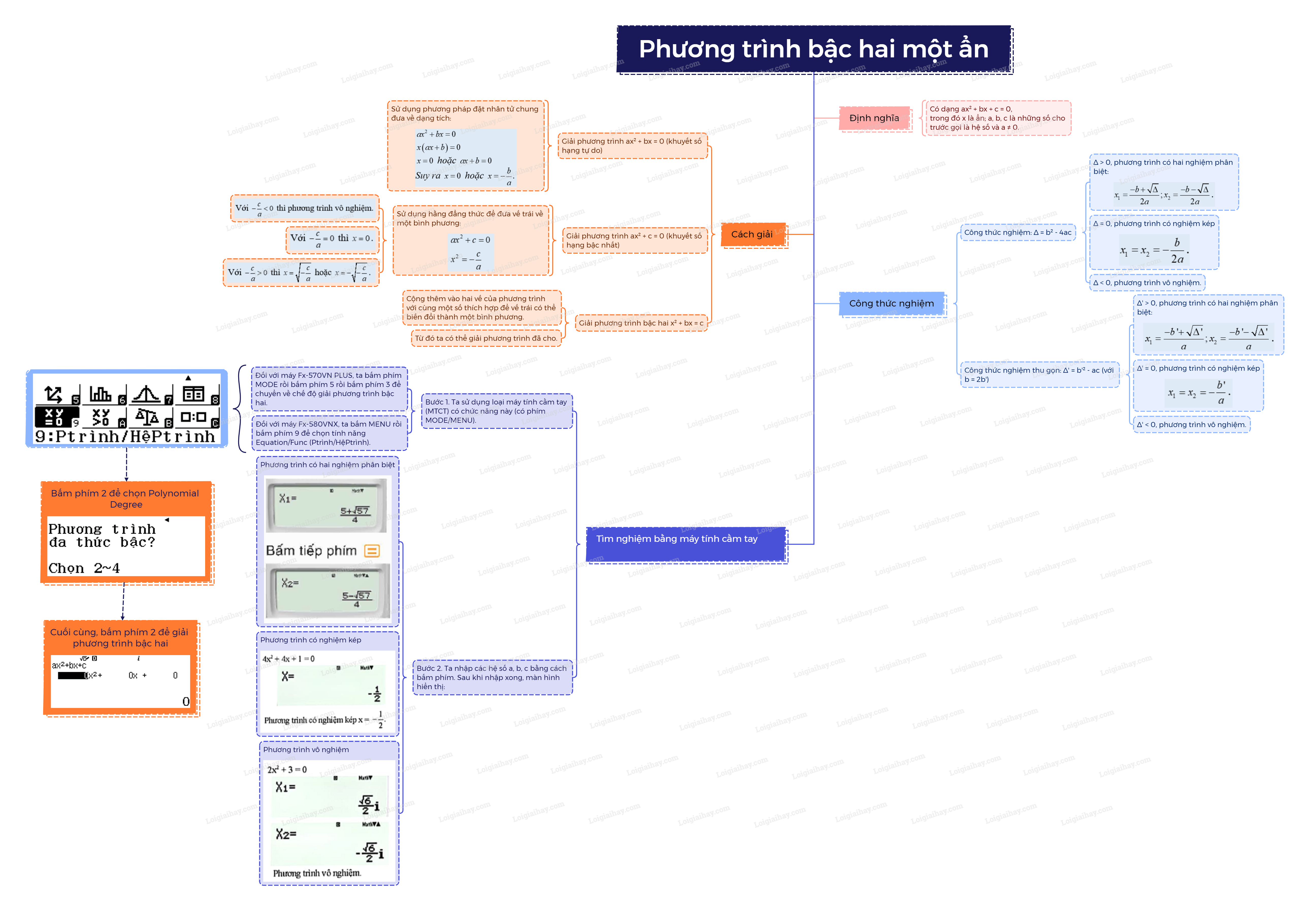
Sơ đồ tư duy Phương trình bậc hai một ẩn

Bài tập Phương trình bậc hai một ẩn

Bài 1. Trong các phương trình sau, phương trình nào là phương trình bậc hai ẩn x?

A. 5x² = 0;

B. $\sqrt{7}{t}^2-6t+4=0;$

C. $\frac{1}{y^2}+\frac{2}{y}-5=0;$

D. 0x² + 6x + 15 = 0.

Hướng dẫn giải

Đáp án đúng là: A

Phương trình 5x² = 0 là phương trình bậc hai ẩn x với các hệ số a = 5, b = c = 0.

Phương trình $\sqrt{7}{t}^2-6t+4=0$ là phương trình bậc hai ẩn t với các hệ số $a=\sqrt{7},b=-6,c=4.$

Phương trình $\frac{1}{y^2}+\frac{2}{y}-5=0$ không là phương trình bậc hai vì có chứa ẩn y dưới mẫu.

Phương trình 0x² + 6x + 15 = 0 không là phương trình bậc hai vì có hệ số a = 0.

Vậy ta chọn phương án A.

Bài 2. Phương trình 4x² – 11x = 0 có nghiệm là

A. x = 0;

B. $x_1=0,x_2=-\frac{11}{4};$

C. $x_1=0,x_2=\frac{11}{4};$

D. $x=-\frac{11}{4}.$

Hướng dẫn giải

Đáp án đúng là: C

Giải phương trình:

4x² – 11x = 0

x(4x – 11) = 0

x = 0 hoặc 4x – 11 = 0

x = 0 hoặc $x=\frac{11}{4}.$

Vậy phương trình có hai nghiệm là $x_1=0,x_2=\frac{11}{4}.$

Do đó ta chọn phương án C.

Bài 3. Để tìm nghiệm của phương trình 0,5x² + 0,625x – 1,1375 = 0, ta bấm lần lượt các phím sau:

A.

B.

C.

D.

Hướng dẫn giải

Đáp án đúng là: D

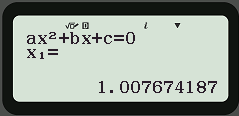
Để tìm nghiệm của phương trình 0,5x² + 0,625x – 1,1375 = 0, ta bấm lần lượt các phím sau:

Màn hình hiện ra kết quả:

Vậy ta chọn phương án D.

Bài 4. Không giải phương trình, hãy nhận xét số nghiệm của các phương trình sau:

a) –22x² + 3151x – 96 = 0;

b) x² + 82x + 1681 = 0;

c) 4x² – 8x + 2048 = 0.

Hướng dẫn giải

a) Ta có: ∆ = b² – 4ac = 3 151² – 4.(–22).(–96) = 9 920 353 > 0.

Vậy phương trình đã cho có hai nghiệm phân biệt.

b) Vì b = 82 nên b’ = 41.

Ta có: ∆’ = b’² – ac = 41² – 1.1681 = 0.

Vậy phương trình đã cho có nghiệm kép.

c) Vì b = –8 nên b’ = –4.

Ta có: ∆’ = b’² – ac = (–4)² – 4.2 048 = –8 176 < 0.

Vậy phương trình đã cho vô nghiệm.

Bài 5. Giải các phương trình sau:

a) (2x – 3)² – 10 = 0;

b) 4x(x + 2) = –15;

c) $x^2-\left(5+\sqrt{3}\right)x+5\sqrt{3}=0;$

d) $x\left(4x+5\right)=3x^2-\frac{25}{4}.$

Hướng dẫn giải

a) (2x – 3)² – 10 = 0

  (2x – 3)² = 10

  $2x-3=\sqrt{10}$ hoặc $2x-3=-\sqrt{10}$

  $2x=3+\sqrt{10}$ hoặc $2x=3-\sqrt{10}$

  $x=\frac{3+\sqrt{10}}{2}$ hoặc $x=\frac{3-\sqrt{10}}{2}.$

Vậy phương trình có hai nghiệm là: $x_1=\frac{3+\sqrt{10}}{2};x_2=\frac{3-\sqrt{10}}{2}.$

b) 4x(x + 2) = –15

  4x² + 8x = –15

  4x² + 8x + 4 = –15 + 4

  (2x + 2)² = –11.

Vì –11 < 0 nên phương trình (2x + 2)² = –11 vô nghiệm.

Vậy phương trình đã cho vô nghiệm.

c) $x^2-\left(5+\sqrt{3}\right)x+5\sqrt{3}=0$

Ta có: $\Delta =b^2-4ac={\left(-\left(5+\sqrt{3}\right)\right)}^2-4\cdot 1\cdot 5\sqrt{3}$

  $=25+10\sqrt{3}+3-20\sqrt{3}=25-10\sqrt{3}+3={\left(5-\sqrt{3}\right)}^2>0.$

  $\sqrt{\Delta }=\sqrt{{\left(5-\sqrt{3}\right)}^2}=\left(5-\sqrt{3}\right)=5-\sqrt{3}.$

Do đó, phương trình có hai nghiệm phân biệt là:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{5+\sqrt{3}+5-\sqrt{3}}{2\cdot 1}=5;$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{5+\sqrt{3}-\left(5-\sqrt{3}\right)}{2\cdot 1}=\sqrt{3}.$

Vậy phương trình có hai nghiệm phân biệt là: $x_1=5;x_2=\sqrt{3}.$

d) $x\left(4x+5\right)=3x^2-\frac{25}{4}$

  $4x^2+5x=3x^2-\frac{25}{4}$

  $x^2+5x+\frac{25}{4}=0.$

Ta có: $\Delta =b^2-4ac=5^2-4\cdot 1\cdot \frac{25}{4}=0.$

Do đó, phương trình $x^2+5x+\frac{25}{4}=0$ có nghiệm kép:

$x_1=x_2=-\frac{b}{2a}=-\frac{5}{2\cdot 1}=-\frac{5}{2}.$

Vậy phương trình đã cho có nghiệm kép: $x_1=x_2=-\frac{5}{2}.$

Bài 6. Ra đa của một máy trực thăng theo dõi chuyển động của một ô tô trong 10 phút, phát hiện rằng tốc độ v (km/h) của ô tô thay đổi phụ thuộc vào thời gian t (phút) được cho bởi công thức v = 3t² – 25t + 98.

a) Tính tốc độ của ô tô khi t = 7.

b) Tính giá trị của t khi tốc độ của ô tô là 150 km/h (theo đơn vị phút và làm tròn kết quả đến hàng phần mười).

Hướng dẫn giải

a) Với t = 7, ta có: v = 3.7² – 25.7 + 98 = 70 (km/h).

Vậy tốc độ của ô tô khi t = 7 là 70 km/h.

b) Theo giả thiết, ta có: v = 150.

Tức là, 3t² – 25t + 98 = 150.

Hay, 3t² – 25t – 52 = 0.

Phương trình trên có ∆ = b² – 4ac = (–25)² – 4.3.(–52) = 1 249 > 0.

Do đó, phương trình 3t² – 25t – 52 = 0 có hai nghiệm phân biệt:

$t_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{25+\sqrt{1249}}{2\cdot 3}\approx 10,1;$

$t_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{25-\sqrt{1249}}{2\cdot 3}\approx -1,7.$

Vì t > 0 nên ta nhận t₁ ≈ 10,1.

Vậy khi tốc độ của ô tô là 150 km/h thì t ≈ 10,1 phút.

Trắc nghiệm: Phương trình bậc hai một ẩn

I. Nhận biết

Câu 1. Phương trình nào dưới đây là phương trình bậc hai một ẩn?

A. $3x^2-3\sqrt{x}+2=0.$

B. $2x^2-2022=0.$

C. $4x+\frac{1}{x}-5=0.$

D. $5x-1=0.$

Câu 2. Khẳng định nào sau đây sai?

A. $x^2-4x-3=0$ trong đó $a=1;b=-4;c=-3.$

B.$4x^2-\sqrt{2}x+1=0$ trong đó $a=4;b=-\sqrt{2};c=1.$

C. $x^2-4x-5=0$ trong đó $a=1;b=-4;c=5.$

D. $\sqrt{5}{x}^2-m-1=0$ trong đó $a=\sqrt{5};b=0;c=-m-1.$

Câu 3.Cho phương trình $a{x}^2+bx+c=0\left(a\ne 0\right)$ có biệt thức $\Delta =b^2-4ac.$Phương trình đã cho có nghiệm khi

A. $\Delta <0.$

B. $\Delta =0.$

C. $\Delta \ge 0.$

D. $\Delta >0.$

Câu 4. Phương trình $4x^2+9=0$ có bao nhiêu nghiệm?

A. vô nghiệm.

B. 1 nghiệm.

C. 2nghiệm.

D. 3nghiệm.

Câu 5. Giả sử $x_1;x_2$là hai nghiệm của phương trình bậc hai $a{x}^2+bx+c=0$ có ${\Delta }^{\text{'}}>0.$Khẳng định nào say đây là đúng?

A. Phương trình có hai nghiệm $x_1=-\frac{b^{\text{'}}+\sqrt{\Delta }}{2a};x_2=-\frac{b^{\text{'}}-\sqrt{\Delta }}{2a}.$

B. Phương trình có hai nghiệm phân biệt $x_1=-\frac{b^{\text{'}}+\sqrt{\Delta }}{2a};x_2=-\frac{b^{\text{'}}-\sqrt{\Delta }}{2a}.$

C. Phương trình có hai nghiệm $x_1=-\frac{b^{\text{'}}+\sqrt{{\Delta }^{\text{'}}}}{2a};x_2=-\frac{b^{\text{'}}-\sqrt{{\Delta }^{\text{'}}}}{2a}.$

D. Phương trình có hai nghiệm phân biệt $x_1=-\frac{b^{\text{'}}+\sqrt{{\Delta }^{\text{'}}}}{2a};x_2=-\frac{b^{\text{'}}-\sqrt{{\Delta }^{\text{'}}}}{2a}.$

II. Thông hiểu

Câu 6. Nghiệm của phương trình $2x^2-5x+2=0$ là

A. $x_1=-2;x_2=-1.$

B. $x_1=2;x_2=-\frac{1}{2}.$

C. $x_1=2;x_2=\frac{1}{2}.$

D. $x_1=-\frac{1}{2};x_2=-2.$

Câu 7. Phương trình $9x^2-30x+25=0$có nghiệm là

A. $x_1=x_2=\frac{5}{3}.$

B. $x_1=x_2=-\frac{5}{3}.$

C. $x_1=x_2=-\frac{3}{3}.$

D. $x_1=x_2=\frac{3}{5}.$

Câu 8. Cho phương trình $3x^2+6x+9=0$. Kết luận nào sau đây đúng?

A. $\Delta =72$ và phương trình có hai nghiệm phân biệt.

B. $\Delta =-72$ và phương trình có hai nghiệm phân biệt.

C. $\Delta =0$ và phương trình có nghiệm kép.

D. $\Delta =-72$ và phương trình vô nghiệm.

Câu 9. Phương trình nào sau đây nhận $x=1$ và $x=-3$ làm nghiệm?

A. $2x^2+6x=0.$

B. $x^2-2x+1=0.$

C. $x^2+2x-3=0.$

D. $\sqrt{3}{x}^2+x-3=0.$

III. Vận dụng

Câu 10. Tích các nghiệm của phương trình $\left(x+2\right)\left(x+3\right)\left(x+5\right)\left(x+6\right)=504$ là

A. 2

B. -2

C. -9

D. 9

Xem thêm tóm tắt lý thuyết Toán lớp 9 sách Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 20: Định lí Viète và ứng dụng

Lý thuyết Bài 21: Giải bài toán bằng cách lập phương trình

Lý thuyết Bài 22: Bảng tần số và biểu đồ tần số

Lý thuyết Bài 23: Bảng tần số tương đối và biểu đồ tần số tương đối

Lý thuyết Bài 24: Bảng tần số, tần số tương đối ghép nhóm và biểu đồ

Xem thêm tài liệu Toán lớp 9:

Giải Toán 9 Bài 19: Phương trình bậc hai một ẩn

Giải SBT Toán 9 Bài 19: Phương trình bậc hai một ẩn

Giáo án Phương trình bậc hai một ẩn lớp 9

Giáo án điện tử Phương trình bậc hai một ẩn lớp 9