Nội dung bài viết

    Xem thêm

    Lý thuyết Hình trụ và hình nón - Toán 9 Kết nối tri thức

    Tóm tắt lý thuyết Toán lớp 9 Bài 31: Hình trụ và hình nón hay, chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 9.

    1 123 14/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 9 Bài 31: Hình trụ và hình nón

    1. Hình trụ

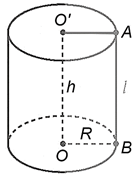
    − Một số yếu tố của hình trụ:

    Hình trụ và hình nón (Lý thuyết Toán lớp 9) | Kết nối tri thức

    Chiều cao: h = O'O.

    Bán kính đáy: R = OB.

    Đường sinh: l = AB.

    − Diện tích xung quanh của hình trụ: Sxq=2πRh.

    Trong đó: R là bán kính đáy;

      h là chiều cao.

    − Thể tích hình trụ: V = Sđáy . h = πR2h.

    Trong đó: Sđáy là diện tích đáy;

      R là bán kính đáy;

      h là chiều cao.

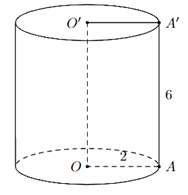
    Ví dụ: Xét hình trụ dưới đây với bán kính đáy là 2 cm, chiều cao 6 cm (như hình vẽ).

    Hình trụ và hình nón (Lý thuyết Toán lớp 9) | Kết nối tri thức

    Tính diện tích xung quanh và thể tích của hình trụ.

    Hướng dẫn giải

    Diện tích xung quanh của hình trụ là:

    Sxq = 2πRh = 2π . 2 . 6 = 24π (cm2)

    Thể tích hình trụ là:

    V = πR2h = π. 22 . 6 = 24π (cm3)

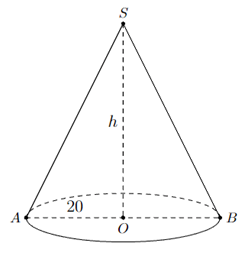
    2. Hình nón

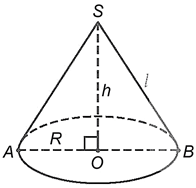
    − Một số yếu tố của hình nón:

    Hình trụ và hình nón (Lý thuyết Toán lớp 9) | Kết nối tri thức

    Đỉnh: S.

    Chiều cao: h = SO.

    Đường sinh: l = SA = SB.

    Bán kính đáy: R = OA.

    − Diện tích xung quanh của hình nón: Sxq = πrl.

    Trong đó: r là bán kính đáy;

      l là độ dài đường sinh.

    − Thể tích hình nón: V=13.Sdáy.h=13πr2h.

    Trong đó: Sđáy là diện tích đáy;

      r là bán kính đáy;

      h là chiều cao.

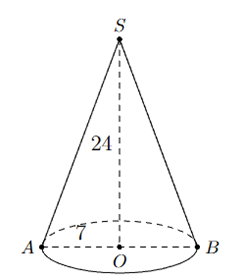
    Ví dụ: Xét một hình nón có bán kính đáy bằng 7 cm, chiều cao bằng 24 cm như sau:

    Hình trụ và hình nón (Lý thuyết Toán lớp 9) | Kết nối tri thức

    Tính diện tích xung quanh và thể tích của hình nón.

    Hướng dẫn giải

    Áp dụng định lý Pythagore, ta tính được độ dài đường sinh hình nón:

    l=R2+h2=72+242=25 (cm).

    Diện tích xung quanh của hình nón là:

    Sxq = πrl = π . 7 . 25 = 175π (cm2).

    Thể tích hình nón là:

    V=13πr2h=13π.72.27=392π(cm3).

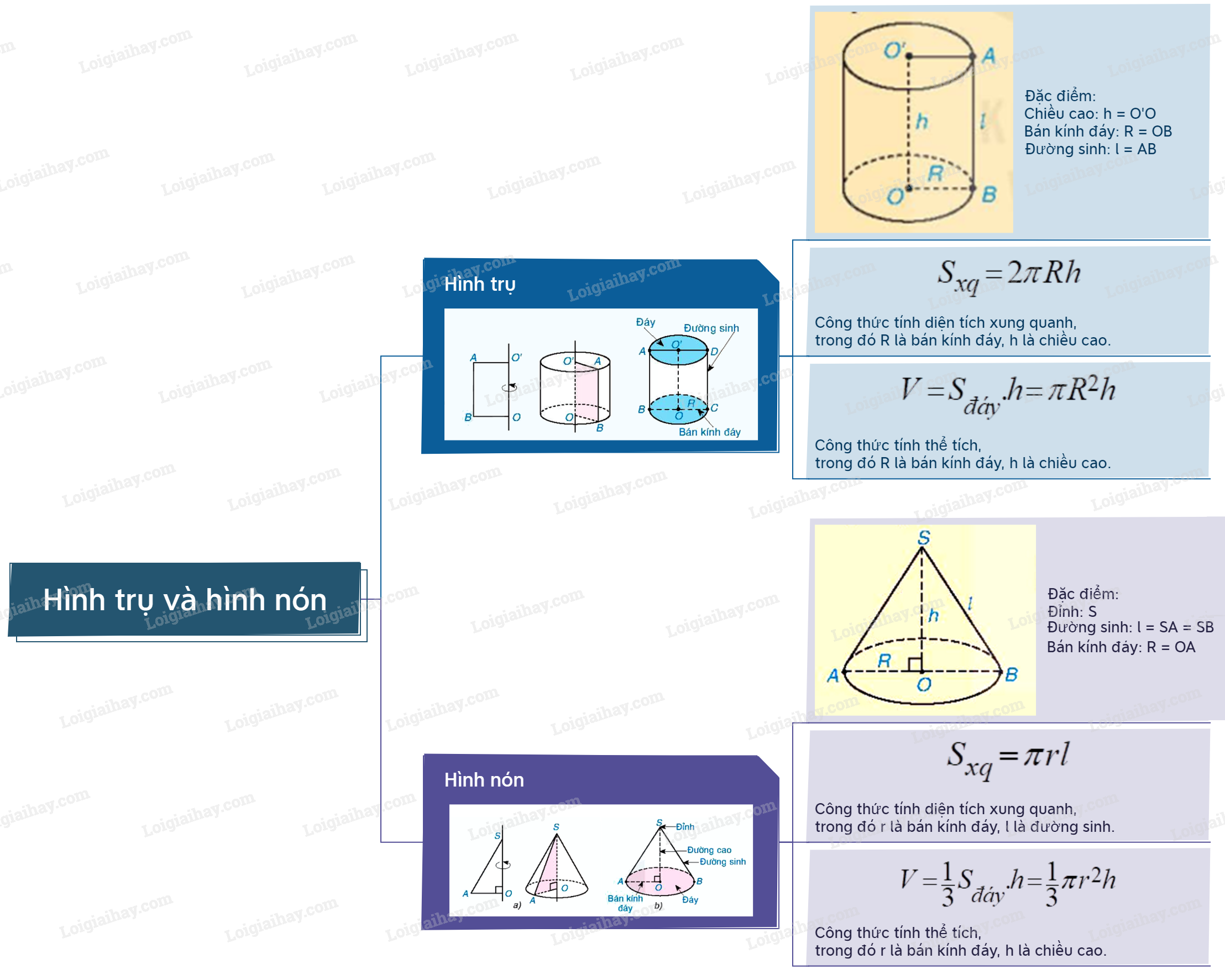
    Sơ đồ tư duy Hình trụ và hình nón

    Lý thuyết Hình trụ và hình nón - Toán 9 Kết nối tri thức (ảnh 1)

    Bài tập Hình trụ và hình nón

    Bài 1. Một hình trụ có diện tích xung quanh là 20π cm2 và diện tích toàn phần là 28π cm2 . Tính thể tích của hình trụ đó.

    A. 20π cm3.

    B. 22π cm3.

    C. 24π cm3.

    D. 25π cm3.

    Hướng dẫn giải

    Đáp án đúng là: A

    Ta có Sđáy = Stp−Sxq2=28π−20π2=4π(cm2)

    Mà Sđáy = πR2 nên 4π = πR2 hay R = 2 (cm).

    Lại có Sxq = 2πRh hay h=20π2πR=102=5 (cm)

    Thể tích của hình trụ đó là:

    V = πR2h = π. 22 . 5 = 20π (cm3).

    Bài 2. Một hình nón có bán kính đáy bằng r, diện tích xung quanh gấp đôi diện tích đáy. Diện tích xung quanh của hình nón tính theo r là

    A. πrl.

    B. 2πr2.

    C. 2πr.

    D. πr2l.

    Hướng dẫn giải

    Đáp án đúng là: B

    Diện tích xung quanh gấp đôi diện tích đáy nên πrl = 2πr2.

    Suy ra l = 2r.

    Do đó πrl = πr · 2r = 2πr2.

    Vậy diện tích xung quanh bằng 2πr2.

    Bài 3. Một hình trụ có chiều cao bằng 5 cm. Biết diện tích toàn phần gấp đôi diện tích xung quanh. Tính thể tích hình trụ.

    Hướng dẫn giải

    Vì diện tích toàn phần bằng hai lần diện tích xung quanh nên

    2πRh + 2πR2 = 4πRh nên 2πR2 = 2πRh hay R = h.

    Do đó, bán kính đáy là 5 cm.

    Thể tích của hình trụ là:

    V = πR2h = π · 52 · 5 = 125π (cm3).

    Vậy thể tích hình trụ là 125π cm3.

    Bài 4. Một hình nón có bán kính đáy bằng 20 cm, số đo thể tích (tính bằng cm2) bằng bốn lần số đo diện tích xung quanh (tính bằng cm2). Tính chiều cao của hình nón.

    Hướng dẫn giải

    Hình trụ và hình nón (Lý thuyết Toán lớp 9) | Kết nối tri thức

    Gọi h là chiều cao của hình nón.

    Thể tích của hình nón bằng:

    V=13πr2h=13π.202.h=4003πh.

    Đường sinh SA bằng h2+202=h2+400 .

    Diện tích xung quanh của hình nón bằng:

    Sxq=π.20.h2+400.

    Do V = 4Sxq nên 4003πh=4π.20.h2+400

      5h=3h2+400

      5h2=9h2+400

      h = 15 (cm)

    Vậy chiều cao của hình nón bằng 15 cm.

    Bài 5. Một thùng phuy hình trụ có số đo diện tích xung quanh (tính bằng mét vuông) đúng bằng số đo thể tích (tính bằng mét khối). Tính bán kính đáy của thùng phuy.

    Hướng dẫn giải

    Gọi bán kính đáy và chiều cao thùng phuy lần lượt là R và h.

    Ta có Sxq = 2πRh (m2);

      V = πR2h (m3).

    Theo đề bài hai số đo trên bằng nhau nên ta có 2πRh = πR2h.

    Suy ra R = 2 (m).

    Vậy bán kính đáy của thùng phuy là 2 m.

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 123 14/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: