Lý thuyết Giải bài toán bằng cách lập phương trình Toán lớp 9 (Kết nối tri thức)

Lý thuyết Toán 9 Bài 21: Giải bài toán bằng cách lập phương trình

Giải bài toán bằng cách lập phương trình

Các bước giải một bài toán bằng cách lập phương trình:

Bước 1. Lập phương trình:

– Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.

– Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.

– Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2. Giải phương trình.

Bước 3. Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.

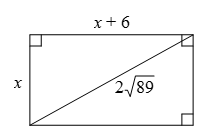
Ví dụ 1. Một sân khấu ngoài trời có dạng hình chữ nhật, chiều dài hơn chiều rộng 6 m, độ dài đường chéo là $2\sqrt{89}$ m.

a) Tính chiều dài và chiều rộng của sân khấu đó.

b) Tính diện tích của sân khấu đó.

Hướng dẫn giải

a) Gọi x (m) là chiều rộng của sân khấu.

Điều kiện: x > 0.

Khi đó, chiều dài của sân khấu đó là x + 6 (m).

Vì độ dài đường chéo của sân khấu đó là $2\sqrt{89}$ m nên theo định lí Pythagore, ta có:

$x^2+{\left(x+6\right)}^2={\left(2\sqrt{89}\right)}^2$

Tức là, x² + x² + 12x + 36 = 356

Hay 2x² + 12x – 320 = 0

Vì b = 12 nên b’ = 6.

Ta có: ∆’ = b’² – ac = 6² – 2.(–320) = 676 > 0 và $\sqrt{{\Delta }^{\text{'}}}=\sqrt{676}=26.$

Do đó, phương trình 2x² + 12x – 320 = 0 có hai nghiệm phân biệt:

$x_1=\frac{-b^{\text{'}}-\sqrt{{\Delta }^{\text{'}}}}{a}=\frac{-6-26}{2}=-16$ (loại);

$x_2=\frac{-b^{\text{'}}+\sqrt{{\Delta }^{\text{'}}}}{a}=\frac{-6+26}{2}=10$ (thỏa mãn điều kiện).

Vậy sân khấu đó có chiều rộng là 10 m và chiều dài là 10 + 6 = 16 m.

b) Diện tích sân khấu đó là: 16.10 = 160 (m²)

Vậy diện tích sân khấu đó bằng 160 m².

Ví dụ 2. Quãng đường từ thành phố A đến thành phố B dài 200 km. Hai ô tô khởi hành cùng một lúc từ A đến B, biết tốc độ ô tô thứ nhất lớn hơn tốc độ ô tô thứ hai là 15 km/h và ô tô thứ nhất đến B trước ô tô thứ hai là 40 phút. Tính tốc độ mỗi xe.

Hướng dẫn giải

Gọi x (km/h) là tốc độ của ô tô thứ hai (x > 0).

Khi đó tốc độ của ô tô thứ nhất là x + 15 (km/h).

Thời gian ô tô thứ hai đi từ thành phố A đến thành phố B là: $\frac{200}{x}$ (giờ).

Thời gian ô tô thứ nhất đi từ thành phố A đến thành phố B là: $\frac{200}{x+15}$ (giờ).

Vì ô tô thứ nhất đến B trước ô tô thứ hai là 40 phút $=\frac{2}{3}$ giờ nên ta có phương trình:

$\frac{200}{x}-\frac{200}{x+15}=\frac{2}{3}.$

Để giải phương trình này, ta quy đồng mẫu vế trái của phương trình:

 $\frac{200\left(x+15\right)-200x}{x\left(x+15\right)}=\frac{2}{3}.$

Nhân cả hai vế của phương trình với 3x(x + 15) để khử mẫu, ta được phương trình:

 600(x + 15) – 600x = 2x(x + 15)

 2x² + 30x – 9 000 = 0

 x² + 15x – 4 500 = 0.

Phương trình trên có: ∆ = b² – ac = 15² – 4.1.(–4 500) = 18 225 > 0;

$\sqrt{\Delta }=\sqrt{18225}=135.$

Suy ra phương trình x² + 15x – 4 500 = 0 có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-15+135}{2\cdot 1}=60$ (thỏa mãn điều kiện);

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-15-135}{2\cdot 1}=-75$ (loại).

Vậy tốc độ của ô tô thứ hai là 60 km/h, tốc độ ô tô thứ nhất là 75 km/h.

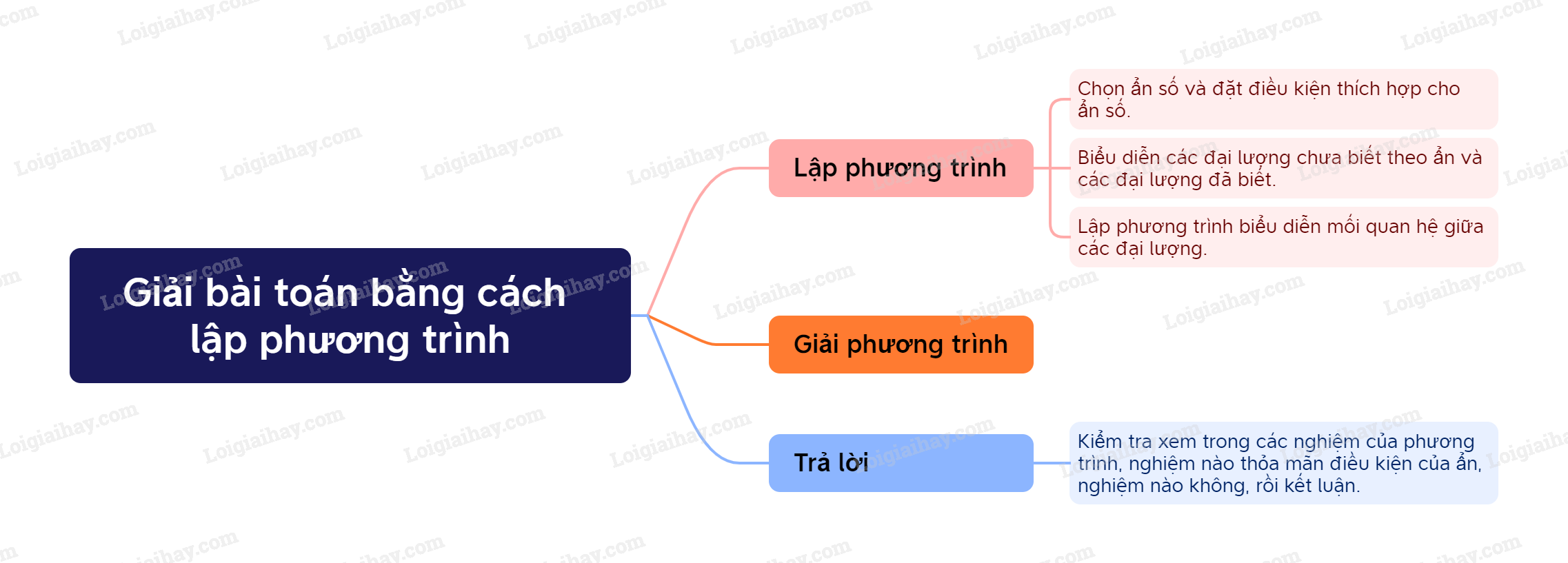
Sơ đồ tư duy Giải bài toán bằng cách lập phương trình

Bài tập Giải bài toán bằng cách lập phương trình

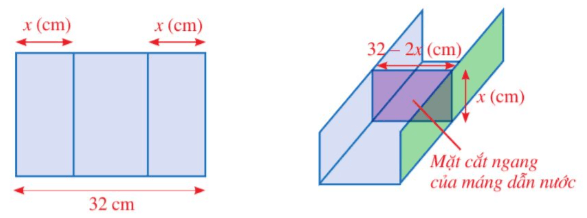
Bài 1. Một người muốn uốn một tấm tôn phẳng có dạng hình chữ nhật với bề ngang là 32 cm thành một máng dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông (như hình vẽ) sao cho 0 < x < 16. Người đó muốn diện tích mặt cắt ngang của máng dẫn nước bằng 120 cm².

Khi đó phương trình bậc hai ẩn x biểu thị diện tích mặt cắt ngang của máng dẫn nước là:

A. –2x² – 32x = 240;

B. –2x² + 32x + 120 = 0;

C. x² + 16x – 60 = 0;

D. x² – 16x + 60 = 0.

Hướng dẫn giải

Đáp án đúng là: D

Diện tích mặt cắt ngang là: (32 – 2x).x (cm²)

Vì diện tích mặt cắt ngang của máng dẫn nước bằng 120 cm² nên ta có phương trình:

(32 – 2x).x = 120, tức là 32x – 2x² – 120 = 0, hay x² – 16x + 60 = 0.

Vậy ta chọn phương án D.

Bài 2. Một công ty vận tải điều một số xe tải để chở 50 tấn hàng. Khi đến kho hàng thì có 3 xe bị hỏng nên để chở hết số hàng thì mỗi xe còn lại phải chở thêm 0,6 tấn so với dự định ban đầu. Giả sử x là số xe công ty vận tải cần điều đi để chở hàng và công ty đó điều đi không quá 25 xe tải. Khi đó điều kiện của ẩn x là:

A. 0 < x < 26;

B. 0 < x ≤ 25 và x ∈ ℕ;

C. 0 < x ≤ 25;

D. 0 < x ≤ 26 và x ∈ ℕ.

Hướng dẫn giải

Đáp án đúng là: B

Gọi x là số xe công ty vận tải cần điều đi để chở hàng, khi đó x ∈ ℕ*.

Mà công ty đó điều đi không quá 25 xe tải nên ta có điều kiện: 0 < x ≤ 25 và x ∈ ℕ.

Vậy ta chọn phương án B.

Bài 3. Nếu đổ thêm 250 g nước vào một dung dịch chứa 50 g muối thì nồng độ dung dịch sẽ giảm 10%. Vậy trước khi đổ thêm nước vào dung dịch thì dung dịch đó có bao nhiêu gam nước?

A. 200 g;

B. 250 g;

C. 300 g;

D. 350 g.

Hướng dẫn giải

Đáp án đúng là: A

Gọi khối lượng nước trong dung dịch trước khi đổ thêm nước là x (g) (x > 0).

Khối lượng dung dịch khi đó là x + 50 (g).

Nồng độ muối trong dung dịch khi đó là: $\frac{50}{x+50}\cdot 100\%.$

Nếu đổ thêm 250 g nước vào dung dịch thì khối lượng của dung dịch là:

x + 50 + 250 = x + 300 (g).

Nồng độ dung dịch lúc này là: $\frac{50}{x+300}\cdot 100\%.$

Vì nồng độ dung dịch giảm 10% nên ta có phương trình:

$\frac{50}{x+50}\cdot 100-\frac{50}{x+300}\cdot 100=10$

$\frac{500\left(x+300\right)}{500\left(x+50\right)\left(x+300\right)}-\frac{500\left(x+50\right)}{500\left(x+50\right)\left(x+300\right)}=\frac{\left(x+50\right)\left(x+300\right)}{500\left(x+50\right)\left(x+300\right)}$

500(x + 300) – 500(x + 50) = (x + 50)(x + 300)

500x + 150 000 – 500x – 25 000 = x² + 300x + 50x + 15 000

x² + 350x – 110 000 = 0.

Vì b = 350 nên b’ = 175.

Ta có: ∆’ = b’² – ac = 175² – 1.(–110 000) = 140 625 > 0 và $\sqrt{{\Delta }^{\text{'}}}=\sqrt{140625}=375.$

Do đó, phương trình x² + 350x – 110 000 = 0 có hai nghiệm phân biệt:

$x_1=\frac{-b^{\text{'}}+\sqrt{{\Delta }^{\text{'}}}}{a}=\frac{-175+375}{1}=200$ (thỏa mãn điều kiện);

$x_2=\frac{-b^{\text{'}}-\sqrt{{\Delta }^{\text{'}}}}{a}=\frac{-175-375}{1}=-550$ (loại).

Vậy trước khi đổ thêm nước vào dung dịch thì dung dịch đó có 200 gam nước.

Do đó ta chọn phương án A.

Bài 4. Một nhà máy chuyên sản xuất một loại sản phẩm. Năm 2019, nhà máy sản xuất được 10 000 sản phẩm. Do ảnh hưởng của dịch bệnh nên sản lượng của nhà máy trong các năm 2020 và 2021 đều giảm, cụ thể: Số lượng sản phẩm thực tế sản xuất được của năm 2020 giảm x% so với số lượng sản phẩm thực tế sản xuất được của năm 2019; Số lượng sản phẩm thực tế sản xuất được của năm 2021 giảm x% so với số lượng sản phẩm thực tế sản xuất được của năm 2020. Biết rằng số lượng sản phẩm thực tế sản xuất được của năm 2021 giảm 65% so với số lượng sản phẩm sản xuất được của năm 2019. Tìm x (làm tròn kết quả đến hàng phần mười).

Hướng dẫn giải

Điều kiện: 0% < x% < 100%.

Do số lượng sản phẩm thực tế sản xuất được của năm 2020 giảm x% so với số lượng sản phẩm sản xuất được của năm 2019 nên số lượng sản phẩm sản xuất được năm 2020 là:

10 000 – 10 000.x% = 10 000 – 100x (sản phẩm).

Do số lượng sản phẩm thực tế sản xuất được của năm 2021 giảm x% so với số lượng sản phẩm thực tế sản xuất được của năm 2020 nên số lượng sản phẩm sản xuất được năm 2021 là:

  10 000 – 100x – (10 000 – 100x).x%

= 10 000 – 100x – 100x + x²

= x² – 200x + 10 000 (sản phẩm).

Do số lượng sản phẩm thực tế sản xuất được của năm 2021 giảm 65% so với số lượng sản phẩm sản xuất được của năm 2019 nên số lượng sản phẩm sản xuất được năm 2021 là:

10 000 – 10 000.65% = 3 500 (sản phẩm).

Khi đó, ta có phương trình: x² – 200x + 10 000 = 3 500.

Giải phương trình:

x² – 200x + 10 000 = 3 500

x² – 200x + 6500 = 0.

Vì b = –200 nên b’ = –100.

Ta có: ∆’ = b’² – ac = (–100)² – 1 . 6 500 = 3 500 > 0.

Do đó, phương trình x² – 200x + 6500 = 0 có hai nghiệm phân biệt:

$x_1=\frac{-b^{\text{'}}+\sqrt{{\Delta }^{\text{'}}}}{a}=\frac{100+\sqrt{3500}}{1}\approx 159,2\%;$

$x_2=\frac{-b^{\text{'}}-\sqrt{{\Delta }^{\text{'}}}}{a}=\frac{100-\sqrt{3500}}{1}\approx 40,8\%.$

Vì 0% < x% < 100% nên ta nhận x ≈ 40,8%.

Vậy x ≈ 40,8 thỏa mãn yêu cầu bài toán.

Bài 5. Một người gửi tiết kiệm 150 triệu đồng kì hạn 12 tháng ở một ngân hàng. Sau kì hạn 12 tháng, tiền lãi của kì hạn đó được cộng vào tiền vốn, rồi người đó tiếp tục đem gửi cho kì hạn 12 tháng tiếp theo. Tổng số tiền người đó nhận được sau khi gửi 24 tháng trên là 172 377 600 đồng. Tìm lãi suất tính theo năm của ngân hàng đó, biết rằng trong 24 tháng đó, lãi suất ngân hàng không thay đổi và người đó không rút tiền ra khỏi ngân hàng.

Hướng dẫn giải

Gọi lãi suất theo năm của ngân hàng đó là x%/năm (x > 0).

Số tiền người đó có được sau khi gửi tiết kiệm 12 tháng đầu tiên là:

$150+150\cdot \frac{x}{100}=150\left(1+\frac{x}{100}\right)$ (triệu đồng).

Số tiền người đó có được sau khi gửi tiết kiệm 24 tháng là:

$150\left(1+\frac{x}{100}\right)+150\left(1+\frac{x}{100}\right).\frac{x}{100}=150\left(1+\frac{x}{100}\right)\left(1+\frac{x}{100}\right)=150{\left(1+\frac{x}{100}\right)}^2$ (triệu đồng).

Vì sau 24 tháng gửi tiết kiệm người đó có tổng số tiền là 172 377 600 đồng = 172,3776 triệu đồng, nên ta có phương trình:

$150{\left(1+\frac{x}{100}\right)}^2=172,3776$

$\frac{3}{200}{\left(100+x\right)}^2=172,3776$

(100 + x)² = 11 491,84

100 + x = 107,2 hoặc 100 + x = –107,2.

x = 7,2 (thỏa mãn) hoặc x = –207,2 (loại).

Vậy lãi suất tính theo năm của ngân hàng đó là 7,2%/năm.

Trắc nghiệm: Giải bài toán bằng cách lập phương trình

I. Nhận biết

Cho bài toán sau, hãy sử dụng để trả lời các câu hỏi từ Câu 1 đến Câu 4

Một mảnh đất hình chữ nhật có độ dài đường chéo là 26 m, chiều dài hơn chiều rộng 14 m. Nếu gọi chiều rộng của mảnh đất là $x$ (m) với $x>0.$ Hãy trả lời các câu hỏi sau để tính được diện tích của mảnh đất.

Câu 1. Chiều dài của mảnh đất hình chữ nhật tính theo là

A. $x+14$ (m).

B. $x-14$(m).

C. $14.x$ (m).

D. $x:14$ (m).

Câu 2. Nếu gọi mảnh đất hình chữ nhật với các đỉnh là $A,B,C,D,$ thì biểu thức nào sau đây biểu diễn độ dài đường chéo của hình chữ nhật?

A. $B{D}^2=A{C}^2+A{B}^2.$

B. $B{D}^2=A{D}^2+A{B}^2.$

C. $B{D}^2=A{D}^2+A{C}^2.$

D. $B{D}^2=A{C}^2-A{B}^2.$

Câu 3. Dựa vào biểu thức biểu diễn độ dài đường chéo ở Câu 2, hãy lập phương trình cho bài toán

A. $x^2+{\left(x-14\right)}^2={26}^2.$

B. $x^2-{\left(x+14\right)}^2={26}^2.$

C. $x^2+{\left(x+14\right)}^2={26}^2.$

D. ${\left(x+7\right)}^2-x^2={26}^2.$

Câu 4. Giải phương trình ở Câu 3, và kết luận về độ dài của chiều dài và rộng của mảnh đất hình chữ nhật.

A. Chiều dài: 24m; chiều rộng: 24 m.

B. Chiều dài: 34m; chiều rộng: 10 m.

C. Chiều dài: 14 m; chiều rộng:7 m.

D. Chiều dài: 24m; chiều rộng:10 m.

Câu 5. Giải một bài toán bằng cách lập phương trình có bao nhiêu bước?

A. 4

B. 5

C. 3

D. 5

II. Thông hiểu

Câu 6. Hai vòi nước cùng chảy vào bể thì 6 giờ đầy bể. Nếu mỗi vòi chảy một mình cho đây bể thì vòi thứ hai cần nhiều hơn vòi thứ nhất 3 giờ. Nếu gọi thời gian vòi thứ nhất chảy một mình đầy bể là $x$ (giờ) với $x>6.$ Phương trình của bài toán này là

A. $\frac{1}{x}+\frac{1}{x+3}=\frac{1}{6}.$

B. $\frac{1}{x}+\frac{1}{x-3}=\frac{1}{6}.$

C. $\frac{1}{x}-\frac{1}{x+3}=\frac{1}{6}.$

D. $\frac{1}{x}-\frac{1}{x-3}=\frac{1}{6}.$

Câu 7. Một đội xe cần phải chuyên chở 150 tấn hàng. Hôm làm việc có 5 xe được điều đi làm việc khác nên mỗi xe còn lại phải chở thêm 5 tấn. Nếu gọi số xe ban đầu là $x$ . Phương trình của bài toán này là

A. $\frac{150}{x+5}-\frac{150}{x}=5$ .

B.$\frac{150}{x-5}-\frac{150}{x}=5$ .

C. $\frac{150}{x-5}+\frac{150}{x}=5$ .

D. $\frac{150}{x+5}+\frac{150}{x}=5$ .

Câu 8. Một phòng họp có 360 ghế ngồi được xếp thành từng dãy và số ghế của từng dãy đều như nhau. Nếu tăng số dãy thêm 1 và số ghế của mỗi dãy tăng thêm 1 thì trong phòng có 400ghế. Nếu gọi số dãy ghế là $x$ (dãy) với $x\in {\mathbb{N}}^{*}.$ Biết số dãy ghế ít hơn, lập phương trình của bài toán là

A. $\left(x-1\right)\left(\frac{360}{x}+1\right)=400$ .

B.$\left(x-1\right)\left(\frac{360}{x}+1\right)=400$ .

C.$\left(x-1\right)\left(\frac{360}{x}+1\right)=400$ .

D. $\left(x-1\right)\left(\frac{360}{x}+1\right)=400$ .

Câu 9. Tìm hai số tự nhiên liên tiếp có tổng các bình phương của nó là 85

A. 4 và 5

B. 8 và 9

C. 6 và 7

D. 7 và 8

III. Vận dụng

Câu 10. Bác An đi xe máy từ nhà đến nơi làm việc cách nhau km với vận tốc dự định trước. Sau khi đi được $\frac{1}{3}$ quãng đưỡng, do điều kiện thời tiết không thuận lợi nên trên quãng đường còn lại bác An phải đi với vận tốc ít hơn so với vận tốc dự định ban đầu 10 km/h. Vận tốc dự định của bác An khi đi từ nhà đến nơi làm việc là bao nhiêu? Biết bác An đến nơi làm việc muộn hơn dự định 20 phút.

A. 70 km/h.

B. 60 km/h.

C. 40 km/h.

D. 30 km/h.

Xem thêm tóm tắt lý thuyết Toán lớp 9 sách Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 22: Bảng tần số và biểu đồ tần số

Lý thuyết Bài 23: Bảng tần số tương đối và biểu đồ tần số tương đối

Lý thuyết Bài 24: Bảng tần số, tần số tương đối ghép nhóm và biểu đồ

Lý thuyết Bài 25: Phép thử ngẫu nhiên và không gian mẫu

Lý thuyết Bài 26: Xác suất của biến cố liên quan tới phép thử

Xem thêm tài liệu Toán lớp 9:

Giải Toán 9 Bài 21: Giải bài toán bằng cách lập phương trình

Giải SBT Toán 9 Giải bài toán bằng cách lập phương trình

Giáo án Giải bài toán bằng cách lập phương trình

Giáo án điện tử Giải bài toán bằng cách lập phương trình