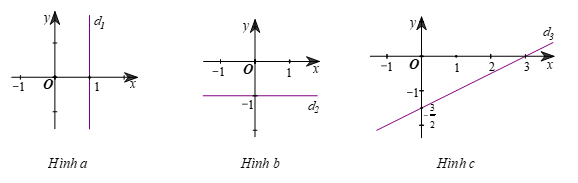Lý thuyết Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn Toán lớp 9 (Kết nối tri thức)

Lý thuyết Toán 9 Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn - Kết nối tri thức

A. Lý thuyết Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

1. Phương trình bậc nhất hai ẩn

Khái niệm phương trình bậc nhất hai ẩn: Phương trình bậc nhất hai ẩn x và y là hệ thức dạng ax + by = c (1), trong đó a, b và c là các số đã biết (a ≠ 0 hoặc b ≠ 0).

Khái niệm nghiệm của phương trình bậc nhất hai ẩn: Nếu tại x = x₀ và y = y₀ ta có ax₀ + by₀ = c là một khẳng định đúng thì cặp số (x₀; y₀) được gọi là một nghiệm của phương trình (1).

Chú ý: Một phương trình bậc nhất hai ẩn đều có vô số nghiệm.

Ví dụ 1. Các phương trình x = 1; 2y = –3; x – 2y = 3 là các phương trình bậc nhất hai ẩn x, y.

Phương trình 0x + 0y = 1 không là phương trình bậc nhất hai ẩn.

Ví dụ 2. Trong các cặp số sau, cặp số nào là nghiệm của phương trình x – 2y = 3?

a) (1; 2);

b) (–1; –2);

c) (3; 0).

Hướng dẫn giải

⦁ Thay x = 1 và y = 2, ta có: 1 – 2.2 = –3 ≠ 3.

Vậy (1; 2) không là nghiệm của phương trình đã cho.

⦁ Thay x = –1 và y = –2, ta có: –1 – 2.(–2) = 3.

Vậy (–1; –2) là một nghiệm của phương trình đã cho.

⦁ Thay x = 3 và y = 0, ta có: 3 – 2.0 = 3.

Vậy (3; 0) là một nghiệm của phương trình đã cho.

Nhận xét: Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ (x; y) thỏa mãn phương trình bậc nhất hai ẩn ax + by = c là một đường thẳng. Đường thẳng đó gọi là đường thẳng ax + by = c.

Ví dụ 3. Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) x + 0y = 1.

b) 0x + y = –1.

c) x – 2y = 3.

Hướng dẫn giải:

a) Xét phương trình x + 0y = 1. (1)

Ta viết gọn (1) thành x = 1. Phương trình này có nghiệm là (1; y) với y ∈ ℝ tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm (1; 0). Ta gọi đó là đường thẳng d₁: x = 1 (hình a).

b) Xét phương trình 0x + y = –1. (2)

Ta viết gọn (2) thành y = –1. Phương trình này có nghiệm là (x; –1) với x ∈ ℝ tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm (0; –1). Ta gọi đó là đường thẳng d₂: y = –1 (hình b).

c) Xét phương trình x – 2y = 3. (3)

Ta viết (3) dưới dạng $y=\frac{1}{2}x-\frac{3}{2}.$ Mỗi cặp số $\left(x;\frac{1}{2}x-\frac{3}{2}\right)$ với x ∈ ℝ tùy ý, là một nghiệm của (3). Khi đó ta nói phương trình (3) có nghiệm tổng quát là $\left(x;\frac{1}{2}x-\frac{3}{2}\right)$ với x ∈ ℝ tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng $y=\frac{1}{2}x-\frac{3}{2}.$ Ta cũng gọi đường thẳng này là đường thẳng d₃: x – 2y = 3.

Để vẽ đường thẳng đó, ta chỉ cần xác định hai điểm tùy ý của nó, chẳng hạn $\left(0;-\frac{3}{2}\right)$ và (3; 0), rồi vẽ đường thẳng đi qua hai điểm đó (hình c).

2. Hệ hai phương trình bậc nhất hai ẩn

Khái niệm hệ hai phương trình bậc nhất hai ẩn: Một cặp gồm hai phương trình bậc nhất hai ẩn ax + by = c và a’x + b’y = c’ được gọi là một hệ hai phương trình bậc nhất hai ẩn. Ta thường viết hệ phương trình đó dưới dạng: $\left\{\begin{array}{l}ax+by=c\\ a^{\text{'}}x+b^{\text{'}}y=c^{\text{'}}.\end{array}\right.\left(*\right)$

Ví dụ 4. Trong các hệ phương trình sau, hệ nào không phải là hệ phương trình bậc nhất hai ẩn? Vì sao?

a) $\left\{\begin{array}{l}\sqrt{2}x+y=1\\ y=2.\end{array}\right.$

b) $\left\{\begin{array}{l}x+y=-1\\ 0x+0y=2.\end{array}\right.$

c)$\left\{\begin{array}{l}x-2y=3\\ -4x+5y=-6.\end{array}\right.$

Hướng dẫn giải

Hệ phương trình $\left\{\begin{array}{l}x+y=-1\\ 0x+0y=2\end{array}\right.$không phải là hệ phương trình bậc nhất hai ẩn vì phương trình thứ hai của hệ là 0x + 0y = 2 không phải là phương trình bậc nhất hai ẩn.

Khái niệm nghiệm của hệ hai phương trình bậc nhất hai ẩn: Mỗi cặp số (x₀; y₀) được gọi là một nghiệm của hệ (*) nếu nó đồng thời là nghiệm của cả hai phương trình của hệ (*).

Lưu ý: Mỗi nghiệm của hệ (*) chính là một nghiệm chung của hai phương trình của hệ (*).

Chú ý: Cặp số (x₀; y₀) là nghiệm của hệ phương trình (*) có nghĩa là điểm có tọa độ (x₀; y₀) vừa thuộc đường thẳng ax + by = c, vừa thuộc đường thẳng a’x + b’y = c’. Vậy điểm có tọa độ (x₀; y₀) là giao điểm của hai đường thẳng ax + by = c và a’x + b’y = c’.

Ví dụ 5. Cho hệ phương trình bậc nhất hai ẩn: $\left\{\begin{array}{l}x-y=20\\ 10x-7y=24.\end{array}\right.$

Trong các cặp số sau, cặp số nào là nghiệm của hệ phương trình đã cho?

a) (0; –20);

b) $\left(-\frac{116}{3};-\frac{176}{3}\right).$

Hướng dẫn giải

a) Ta thấy khi x = 0 và y = –20 thì:

0 – (–20) = 20 nên (0; –20) là nghiệm của phương trình thứ nhất;

10.0 – 7.(–20) = 140 ≠ 24 nên (0; –20) không là nghiệm của phương trình thứ hai.

Do đó cặp số (0; –20) không là nghiệm chung của hai phương trình trong hệ.

Vậy cặp số (0; –20) không là nghiệm của hệ phương trình đã cho.

b) Ta thấy khi $x=-\frac{116}{3}$ và $y=-\frac{176}{3}$ thì:

$-\frac{116}{3}–\left(–\frac{176}{3}\right)=20$ nên $\left(-\frac{116}{3};-\frac{176}{3}\right)$ là nghiệm của phương trình thứ nhất;

$10\cdot \left(-\frac{116}{3}\right)–7\cdot \left(–\frac{176}{3}\right)=24$ nên $\left(-\frac{116}{3};-\frac{176}{3}\right)$ là nghiệm của phương trình thứ hai.

Suy ra cặp số $\left(-\frac{116}{3};-\frac{176}{3}\right)$ là nghiệm chung của hai phương trình trong hệ.

Vậy cặp số $\left(-\frac{116}{3};-\frac{176}{3}\right)$ là nghiệm của hệ phương trình đã cho.

B. Bài tập Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

Bài 1. Đường thẳng biểu diễn tất cả các nghiệm của phương trình x – 3y = 2 là đường thẳng

A. song song với trục tung.

B. song song với trục hoành.

C. đi qua gốc tọa độ.

D. đi qua điểm A(–1; –1).

Hướng dẫn giải

Đáp án đúng là: D

Thay x = –1 và y = –1 vào phương trình ta có:

–1 – 3.(–1) = 2.

Vậy đường thẳng x – 3y = 2 đi qua điểm A(–1; –1).

Bài 3. Cặp số nào sau đây là nghiệm của hệ phương trình bậc nhất hai ẩn $\left\{\begin{array}{l}4x-5y=3\\ 3x-y=16\end{array}\right.?$

A. (–1; 3).

B. (2; 1).

C. (7; 5).

D. (5; –1).

Hướng dẫn giải

Đáp án đúng là: C

⦁ Khi x = –1 và y = 3 thì:

4.(–1) – 5.3 = –19 ≠ 3 nên (–1; 3) không là nghiệm của phương trình thứ nhất;

3.(–1) – 3 = –6 ≠ 16 nên (–1; 3) không là nghiệm của phương trình thứ hai.

Do đó cặp số (–1; 3) không là nghiệm chung của hai phương trình trong hệ.

Vậy cặp số (–1; 3) không là nghiệm của hệ phương trình đã cho.

⦁ Khi x = 2 và y = 1 thì:

4.2 – 5.1 = 3 nên (2; 1) là nghiệm của phương trình thứ nhất;

3.2 – 1 = 5 ≠ 16 nên (2; 1) không là nghiệm của phương trình thứ hai.

Do đó cặp số (2; 1) không là nghiệm chung của hai phương trình trong hệ.

Vậy cặp số (2; 1) không là nghiệm của hệ phương trình đã cho.

⦁ Khi x = 7 và y = 5 thì:

4.7 – 5.5 = 3 nên (7; 5) là nghiệm của phương trình thứ nhất;

3.7 – 5 = 16 nên (7; 5) là nghiệm của phương trình thứ hai.

Suy ra cặp số (7; 5) là nghiệm chung của hai phương trình trong hệ.

Vậy cặp số (7; 5) là nghiệm của hệ phương trình đã cho.

⦁ Khi x = 5 và y = –1 thì:

4.5 – 5.(–1) = 25 ≠ 3 nên (5; –1) không là nghiệm của phương trình thứ nhất;

3.5 – (–1) = 16 nên (5; –1) là nghiệm của phương trình thứ hai.

Do đó cặp số (5; –1) không là nghiệm chung của hai phương trình trong hệ.

Vậy cặp số (5; –1) không là nghiệm của hệ phương trình đã cho.

Ta chọn phương án C.

Bài 4. Xét trò ném đồng xu vào trong vòng tròn như hình vẽ dưới đây:

– Lượt chơi thứ nhất (ném đồng xu 2 lần): một đồng xu rơi vào phần trong (hình tròn màu trắng), một đồng xu rơi vào phần ngoài (hình vành khăn màu đen); tổng số điểm đạt được là 17 (điểm).

– Lượt chơi thứ hai (ném đồng xu 5 lần): hai đồng xu rơi vào phần trong, ba đồng xu rơi vào phần ngoài; tổng số điểm đạt được là 41 (điểm).

Gọi x, y lần lượt là số điểm ấn định cho phần trong và phần ngoài.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (10; 7) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Hướng dẫn giải

a) – Lượt chơi thứ nhất có một đồng xu rơi vào phần trong và một đồng xu rơi vào phần ngoài, đạt được 17 điểm nên ta có phương trình: x + y = 17.

– Lượt chơi thứ hai có hai đồng xu rơi vào phần trong, ba đồng xu rơi vào phần ngoài, đạt được 41 điểm nên ta có phương trình: 2x + 3y = 41.

Vậy hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng là: $\left\{\begin{array}{l}x+y=17\\ 2x+3y=41.\end{array}\right.$

b) Thay x = 10 và y = 7 vào mỗi phương trình trong hệ ở câu a, ta có:

10 + 7 = 17;

2.10 + 3.7 = 41.

Suy ra cặp số (10; 7) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (10; 7) là nghiệm của hệ phương trình ở câu a.

Bài 1. Cặp số nào sau đây là nghiệm của phương trình 5x + 4y = 8?

A. (–2; 1).

B. (0; 2).

C. (–1; 0).

D. (4; 3).

Hướng dẫn giải

Đáp án đúng là: B

Xét phương trình 5x + 4y = 8:

⦁ Thay x = –2 và y = 1, ta có: 5.(–2) + 4.1 = –2 ≠ 8.

⦁ Thay x = 0 và y = 2, ta có: 5.0 + 4.2 = 8.

⦁ Thay x = –1 và y = 0, ta có: 5.(–1) + 4.0 = –5 ≠ 8.

⦁ Thay x = 4 và y = 3, ta có: 5.4 + 4.3 = 32 ≠ 8.

Vậy (0; 2) là nghiệm của phương trình đã cho.

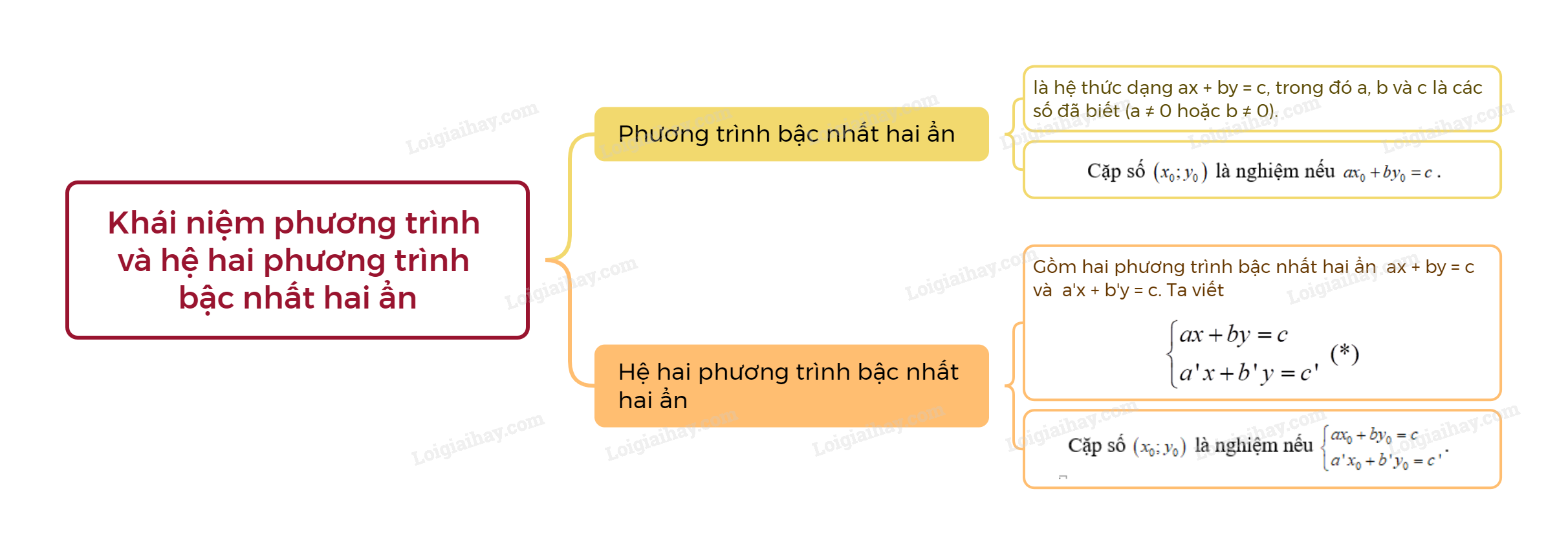
C. Sơ đồ tư duy Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

Trắc nghiệm: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

I. Nhận biết

Câu 1. Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất hai ẩn?

A. x + 2y = 1.

B. 0x - 0y = 5.

C. 0x - y = 3.

D. x + 0y = - 6.

Hiển thị đáp án

Đáp án đúng là: B

Phương trình 0x - 0y = 5 không phải là phương trình bậc nhất hai ẩn do a, b đồng thời bằng 0.

Câu 2. Hệ số a, b, c tương ứng của phương trình bậc nhất hai ẩn x + 2y -1 = 0 là

A. a = 1; b = 1; c = 0.

B. a = 1; b = 2; c = 1.

C. a = 1; b = 2; c = -1.

D. a = 1; b = -2; c = 1.

Hiển thị đáp án

Đáp án đúng là: B

Phương trình bậc nhất hai ẩn x + 2y - 1 = 0 nên a = 1; b = 2; c = -1.

Câu 3. Cặp số nào sau đây là nghiệm của phương trình ?

A. (0; 1).

B. (1; 0).

C. (1; 1).

D. (- 1; 0).

Hiển thị đáp án

Đáp án đúng là: C

⦁ Thay x = 0 và y =1 vào phương trình 2x - y -1 = 0 ta được .

Do đó (0; 1) không phải là nghiệm phương trình đã cho.

⦁ Thay x = 1 và y = 0 vào phương trình 2x - y - 1 = 0 ta được .

Do đó (1; 0) không phải là nghiệm phương trình.

⦁ Thay x = 1 và y = 1 vào phương trình 2x - y - 1 = 0 ta được .

Do đó (1; 1) là nghiệm phương trình đã cho.

⦁ Thay x = -1 và y = 0 vào phương trình 2x - y - 1 = 0 ta được .

Do đó (-1; 0) không phải là nghiệm phương trình đã cho.

Vậy ta chọn phương án C.

Câu 4. Trong các hệ phương trình sau, hệ nào không phải là hệ phương trình bậc nhất hai ẩn?

A.

B.

C.

D.

Hiển thị đáp án

Đáp án đúng là: C

Ta thấy hệ phương trình có chứa số hạng có bậc của x, y là 2 nên không phải là phương trình bậc nhất hai ẩn.

Câu 5. Cho hệ phương trình , cặp số nào sau đây là nghiệm của hệ phương trình đã cho?

A. (0; 1).

B. (2; 2).

C. (3; - 3).

D. (- 2; 2).

Hiển thị đáp án

Đáp án đúng là: D

⦁ Thay x = 0 và y = 1 vào phương trình x + y = 0 ta được nên cặp số (0; 1) không phải là nghiệm của phương trình x + y = 0. Do đó cặp số (0; 1) không phải là nghiệm của hệ phương trình đã cho.

⦁ Thay x = 2 và y = 2 vào phương trình x + y = 0 ta được nên cặp số (2; 2) không phải là nghiệm của phương trình x + y = 0. Do đó cặp số (2; 2) không phải là nghiệm của hệ phương trình đã cho.

⦁ Thay x = 3 và y = - 3 vào phương trình x + 3y = 4 ta được nên cặp số (3; - 3) không phải là nghiệm của phương trình x + 3y = 4. Do đó cặp số (3; - 3) không phải là nghiệm của hệ phương trình đã cho.

⦁ Thay x = - 2 và y = 2 vào từng phương trình của hệ phương trình đã cho, ta được:

- 2 + 2 = 0;

- 2 + 3. 2= 4.

Do đó cặp số (- 2; 2) là nghiệm chung của hai phương trình nên (-2; 2) là một nghiệm của hệ phương trình đã cho.

II. Thông hiểu

Câu 6. Tất cả các nghiệm của phương trình 2x - 3y = 1 được biểu diễn bằng đường thẳng nào dưới đây?

A. y = - 2x +1.

B. y = 2x - 1.

C.

D.

Hiển thị đáp án

Đáp án đúng là: C

Từ phương trình 2x - 3y = 1 ta có 3y = 2x - 1 suy ra

Do đó, tất cả các nghiệm của phương trình 2x - 3y = 1 được biểu diễn bởi đường thẳng

Câu 7. Tất cả các nghiệm của phương trình 0x + 5y = 2 được biểu diễn bởi

A. đường thẳng

B. đường thẳng x = 2 - 5y.

C. đường thẳng

D. đường thẳng .

Hiển thị đáp án

Đáp án đúng là: A

Từ phương trình 0x + 5y = 2 ta có 5y = 2 suy ra

Do đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng .

Câu 8. Tất cả các nghiệm của phương trình 3x - 0y = 1 được biểu diễn bởi

A. đồ thị của hàm số .

B. đồ thị của hàm số

C. đồ thị của hàm số

D. đồ thị của hàm số y = 1 - 3x.

Hiển thị đáp án

Đáp án đúng là: B

Từ phương trình 3x - 0y = 1 ta có 3x = 1 suy ra

Do đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đồ thị của hàm số .

Câu 9. Giá trị nào của để cặp số là nghiệm của phương trình ?

A. .

B. .

C. .

D. .

Hiển thị đáp án

Đáp án đúng là: C

Để cặp số là nghiệm của phương trình thì x = 1 và thỏa mãn phương trình - 3x + 2y = 7.

Thay x = 1 và vào phương trình đó, ta được:

suy ra nên .

III. Vận dụng

Câu 10. Cho phương trình có nghiệm (- 2; 6) . Có bao nhiêu giá trị m thỏa mãn điều kiện trên?

A. 0.

B. 1.

C. 2.

D. 3.

Hiển thị đáp án

Đáp án đúng là: C

Thay x = 2, y = 6 vào phương trình đã cho, ta được:.

Giải phương trình

hoặc m + 2 = 0

m = 1 hoặc m = 2

Vậy có hai giá trị m thỏa mãn yêu cầu đề bài.

Do đó ta chọn phương án C.

Xem thêm tóm tắt lý thuyết Toán lớp 9 sách Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 2: Giải hệ hai phương trình bậc nhất hai ẩn

Lý thuyết Bài 3: Giải bài toán bằng cách lập hệ phương trình

Lý thuyết Bài 4: Phương trình quy về phương trình bậc nhất một ẩn

Lý thuyết Bài 5: Bất đẳng thức và tính chất

Lý thuyết Bài 6: Bất phương trình bậc nhất một ẩn

Xem thêm tài liệu Toán lớp 9:

Giải Toán 9 Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

Giải SBT Toán 9 Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

Giáo án Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn lớp 9

Giáo án điện tử Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn lớp 9