Lý thuyết Góc nội tiếp Toán 9 (Kết nối tri thức)

Lý thuyết Toán 9 Bài 27: Góc nội tiếp

1. Định nghĩa góc nội tiếp và cung bị chắn

Định nghĩa góc nội tiếp: Góc nội tiếp của đường tròn là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Định nghĩa cung bị chắn: Cung nằm bên trong góc được gọi là cung bị chắn.

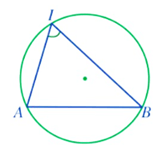
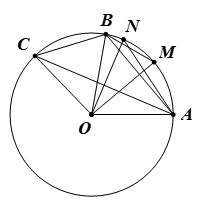
Ví dụ 1.

Ở hình vẽ trên, ta có:

⦁$\widehat{AIB}$ là góc nội tiếp của đường tròn vì có đỉnh I thuộc đường tròn và hai cạnh IA, IB chứa hai dây cung của đường tròn; $\widehat{AIB}$ chắn cung nhỏ AB.

⦁$\widehat{AIB}$ là góc nội tiếp của đường tròn vì có đỉnh A thuộc đường tròn và hai cạnh AI, AB chứa hai dây cung của đường tròn đó; $\widehat{IAB}$ chắn cung nhỏ IB.

⦁$\widehat{IBA}$ là góc nội tiếp của đường tròn vì có đỉnh B thuộc đường tròn và hai cạnh BI, BA chứa hai dây cung của đường tròn đó; $\widehat{IBA}$ chắn cung nhỏ IA.

2. Định líliên hệ giữa góc nội tiếp với cung bị chắn

Định lí: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

Nhận xét: Từ định lí trên ta có các khẳng định sau đối với các góc nội tiếp của một đường tròn hoặc của hai đường tròn bằng nhau:

⦁ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

⦁ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

⦁ Các góc nội tiếp chắn cung nhỏ thì có số đo bằng nửa số đo của góc ở tâm chắn cùng một cung.

⦁ Góc nội tiếp chắn nửa đường tròn là góc vuông.

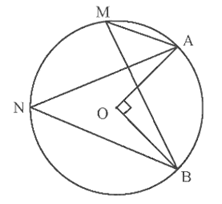
Ví dụ 2. Tính số đo của $\widehat{AMB}$ và $\widehat{ANB}$ trong hình vẽ dưới đây.

Hướng dẫn giải

Quan sát hình vẽ, ta có $\widehat{AOB}=90°.$

Xét đường tròn (O), có$\widehat{AMB}$ và $\widehat{AOB}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ AB nên ta có $\widehat{AMB}=\frac{1}{2}\cdot \widehat{AOB}=\frac{1}{2}\cdot 90°=45°.$

Vì hai góc nội tiếp $\widehat{AMB}$ và $\widehat{ANB}$ cùng chắn cung nhỏ AB nên $\widehat{ANB}=\widehat{AMB}=45°.$

Vậy $\widehat{AMB}=\widehat{ANB}=45°.$

Sơ đồ tư duy Góc nội tiếp

Bài tập Góc nội tiếp

Bài 1. Khẳng định nào sau đây là sai?

A. Góc nội tiếp của đường tròn là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn;

B. Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của cung bị chắn;

C. Trong một đường tròn, các góc nội tiếp chắn các cung bằng nhau thì bằng nhau;

D. Trong một đường tròn, góc nội tiếp chắn cung nhỏ có số đo bằng số đo của góc ở tâm chắn cùng một cung.

Hướng dẫn giải

Đáp án đúng là: D

Phương án A, B, C đúng.

Phương án D sai. Sửa lại: Góc nội tiếp chắn cung nhỏ có số đo bằng nửa số đo của góc ở tâm chắn cùng một cung.

Vậy ta chọn phương án D.

Bài 2. Góc nội tiếp chắn nửa đường tròn là

A. góc vuông;

B. góc nhọn;

C. góc bẹt;

D. góc tù.

Hướng dẫn giải

Đáp án đúng là: A

Góc nội tiếp chắn nửa đường tròn là góc vuông.

Do đó ta chọn phương án A.

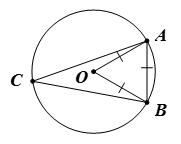
Bài 3. Cho đường tròn (O; R) và dây AB = R. Lấy điểm C thuộc cung lớn AB (C ≠ A, B). Số đo $\widehat{ACB}$ bằng

A. 45°;

B. 30°;

C. 60°;

D. 90°.

Hướng dẫn giải

Đáp án đúng là: B

Ta có OA = OB = AB = R.

Suy ra tam giác OAB đều.Do đó $\widehat{AOB}=60°.$

Xét đường tròn (O), có$\widehat{ACB}$ và $\widehat{AOB}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ AB nên ta có $\widehat{ACB}=\frac{1}{2}\cdot \widehat{AOB}=\frac{1}{2}\cdot 60°=30°.$

Vậy ta chọn phương án B.

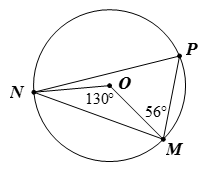
Bài 4. Xác định số đo các góc của tam giác MNP trong hình vẽ bên dưới.

Hướng dẫn giải

Xét đường tròn (O), có$\widehat{MPN}$ và $\widehat{MON}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ MN nên ta có $\widehat{MPN}=\frac{1}{2}\cdot \widehat{MON}=\frac{1}{2}\cdot 130°=65°.$

Vì OM = ON nên tam giác OMN cân tại O.

Suy ra $\widehat{OMN}=\widehat{ONM}.$

Tam giác OMN, có: $\widehat{MON}+\widehat{OMN}+\widehat{ONM}=180°$ (tổng ba góc của một tam giác)

Suy ra $2\widehat{ONM}=180°-\widehat{MON}=180°-130°=50°.$

Do đó $\widehat{OMN}=\widehat{ONM}=\frac{50°}{2}=25°.$

Vì vậy $\widehat{NMP}=\widehat{OMN}+\widehat{OMP}=25°+56°=81°.$

Tam giác MNP, có: $\widehat{MNP}+\widehat{NMP}+\widehat{MPN}=180°$ (tổng ba góc của một tam giác)

Suy ra $\widehat{MNP}=180°-\left(\widehat{NMP}+\widehat{MPN}\right)=180°-\left(81°+65°\right)=34°.$

Vậy $\widehat{MPN}=65°;\widehat{NMP}=81°;\widehat{MNP}=34°.$

Bài 5. Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho $\widehat{AOB}=80°,\widehat{BOC}=54°,$ điểm B thuộc cung nhỏ AC. Gọi M, N lần lượt là hai điểm trên hai cung nhỏ AB, AC và chia mỗi cung đó thành hai cung bằng nhau. Tìm số đo các góc sau:

a) $\widehat{ACB},\widehat{BAC};$

b) $\widehat{ABM},\widehat{BAN}.$

Hướng dẫn giải

a) Xét đường tròn (O), có$\widehat{ACB}$ và $\widehat{AOB}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ AB nên ta có $\widehat{ACB}=\frac{1}{2}\cdot \widehat{AOB}=\frac{1}{2}\cdot 80°=40°.$

Ta cũng có$\widehat{BAC}$ và $\widehat{BOC}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ BC nên $\widehat{BAC}=\frac{1}{2}\cdot \widehat{BOC}=\frac{1}{2}\cdot 54°=27°.$

Vậy $\widehat{ACB}=40°;\widehat{BAC}=27°.$

b) Điểm M chia cung nhỏ AB thành hai cung bằng nhau nên

$\text{sđ}\stackrel{⏜}{AM}=\text{sđ}\stackrel{⏜}{MB}=\frac{1}{2}\text{sđ}\stackrel{⏜}{AB}=\frac{1}{2}\cdot \widehat{AOB}=40°.$

Ta có $\widehat{ABM}$ là góc nội tiếp chắn cung nhỏ AM trong đường tròn (O) nên

$\widehat{ABM}=\frac{1}{2}\text{sđ}\stackrel{⏜}{AM}=\frac{1}{2}\cdot 40°=20°.$

Ta có $\widehat{AOC}=\widehat{AOB}+\widehat{BOC}=80°+54°=134°.$

Điểm N chia cung nhỏ AC thành hai cung bằng nhau nên

$\text{sđ}\stackrel{⏜}{AN}=\text{sđ}\stackrel{⏜}{NC}=\frac{1}{2}\text{sđ}\stackrel{⏜}{AC}=\frac{1}{2}\cdot \widehat{AOC}=67°.$

Ta thấy $\text{sđ}\stackrel{⏜}{AN}<\text{sđ}\stackrel{⏜}{AB}=\widehat{AOB}$ nên điểm N nằm trên cung nhỏ AB.

Khi đó $\text{sđ}\stackrel{⏜}{NB}=\text{sđ}\stackrel{⏜}{AB}-\text{sđ}\stackrel{⏜}{AN}=\widehat{AOB}-67°=80°-67°=13°.$

Mà$\widehat{BAN}$ là góc nội tiếp chắn cung nhỏ NB nên $\widehat{BAN}=\frac{1}{2}\text{sđ}\stackrel{⏜}{NB}=\frac{1}{2}\cdot 13°=6,5°.$

Vậy $\widehat{ABM}=20°;\widehat{BAN}=6,5°.$

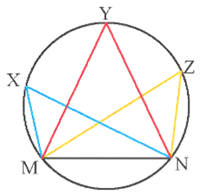
Bài 6. Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn MN (như hình vẽ). Giả sử bóng được đặt ở điểm X thì $\widehat{MXN}$ gọi là góc sút từ vị trí X. Hãy so sánh các góc sút $\widehat{MXN},\widehat{MYN},\widehat{MZN}.$

Hướng dẫn giải

Vì các góc $\widehat{MXN},\widehat{MYN},\widehat{MZN}$ là các góc nội tiếp cùng chắn cung nhỏ MN trong đường tròn nên $\widehat{MXN}=\widehat{MYN}=\widehat{MZN}.$

Vậy các góc sút $\widehat{MXN},\widehat{MYN},\widehat{MZN}$ có số đo bằng nhau.

Trắc nghiệm: Góc nội tiếp

I. Nhận biết

Câu 1. Góc nội tiếp nhỏ hơn hoặc bằng $90°$ có số đo

A. bằng nửa số đo góc ở tâm cùng chắn một cung.

B. bằng số đo của góc ở tâm cùng chắn một cung.

C. bằng số đo cung bị chắn.

D. bằng nửa số đo cung lớn.

Câu 2. Góc nội tiếp chắn nửa đường tròn có số đo bằng

A. $45°$.

B. $90°$.

C. $60°$.

D. $120°$.

Câu 3. Trong các hình dưới đây, hình biểu diễn góc nội tiếp là

A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Câu 4. Khẳng định nào sau đây là sai?

A. Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.

B. Trong một đường tròn, hai góc nội tiếp bằng nhau chắn hai cung bằng nhau.

C. Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.

D. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.

Câu 5. Cung nằm bên trong góc nội tiếp được gọi là

A. cung ngoại tiếp.

B. cung nội tiếp.

C. cung chắn.

D. cung bị chắn.

II. Thông hiểu

Câu 6. Cho đường tròn $\left(O\right)$ và điểm $I$nằm ngoài $\left(O\right)$. Từ điểm $I$ kẻ hai dây cung $AB$ và $CD$ ($A$ nằm giữa $I$ và $B$, $C$ nằm giữa $I$ và $D$). Tích $IA\cdot IB$ bằng

A. $ID\cdot CD$.

B. $IC\cdot CB$.

C. $IC\cdot CD$.

D. $IC\cdot ID$.

Câu 7. Cho tam giác $ABC$ có ba góc nhọn, đường cao $AH$ và nội tiếp đường tròn tâm $\left(O\right)$, đường kính $AM$. Số đo góc $\widehat{ABM}$ là

A. $90°$.

B. $80°$.

C. $110°$.

D. $120°$.

Câu 8. Cho $\left(O\right)$, đường kính $AB$, điểm $D$ thuộc đường tròn sao cho $\widehat{DAB}=50°$. Gọi $E$ là điểm đối xứng với $A$ qua $D$. Số đo góc $AEB$ bằng

A. $50°$.

B. $60°$.

C. $45°$.

D. $70°$.

Câu 9. Cho tam giác $ABC$ nhọn có ba đỉnh nằm trên đường tròn $\left(O\right)$. Hai đường cao $BD$ và $CE$ cắt nhau tại $H$. Vẽ đường kính $AF$. Khẳng định nào sau đây là đúng?

A.$BH=BE$.

B.$BH=CF$.

C.$BH=CH$.

D.$HF=BC$.

III. Vận dụng

Câu 10. Cho tam giác nhọn $ABC$có ba đỉnh nằm trên đường tròn $\left(O\right)$. Hai đường cao $BD$ và $CE$ cắt nhau tại $H$. Vẽ đường kính $AF$ và gọi $M$ là trung điểm $BC$. Cho các khẳng định sau:

(i) $OM\perp BC$.

(ii) $OM\text{//}AH$.

(iii) $HM=\frac{HF}{2}$.

Có bao nhiêu khẳng định đúng trong các khẳng định trên?

A. 0.

B. 1.

C. 2.

D. 3.

Xem thêm tóm tắt lý thuyết Toán lớp 9 sách Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác

Lý thuyết Bài 29: Tứ giác nội tiếp

Lý thuyết Bài 30: Đa giác đều

Lý thuyết Bài 31: Hình trụ và hình nón

Lý thuyết Bài 32: Hình cầu

Xem thêm tài liệu Toán lớp 9:

Giải Toán 9 Bài 27: Góc nội tiếp

Giải SBT Toán 9 Bài 27: Góc nội tiếp

Giáo án Góc nội tiếp lớp 9

Giáo án điện tử Góc nội tiếp lớp 9