Lý thuyết Giải hệ hai phương trình bậc nhất hai ẩn – Toán lớp 9 Kết nối tri thức

Lý thuyết Toán 9 Bài 2: Giải hệ hai phương trình bậc nhất hai ẩn - Kết nối tri thức

A. Lý thuyết Giải hệ hai phương trình bậc nhất hai ẩn

1. Phương pháp thế

Cách giải hệ phương trình bằng phương pháp thế:

Bước 1. Từ một phương trình của hệ, biểu diễn một ẩn theo ẩn kia rồi thế vào phương trình còn lại của hệ để được phương trình chỉ còn chứa một ẩn.

Bước 2. Giải phương trình một ẩn vừa nhận được, từ đó suy ra nghiệm của hệ phương trình đã cho.

Ví dụ 1. Giải hệ phương trình $\left\{\begin{array}{l}2x+3y=7\\ x-10y=-8\end{array}\right.$bằng phương pháp thế.

Hướng dẫn giải

Giải hệ phương trình $\left\{\begin{array}{l}2x+3y=7\left(1\right)\\ x-10y=-8\left(2\right)\end{array}\right.$

Từ phương trình (2), ta có: x = 10y – 8. (3)

Thế vào phương trình (1) ta được: 2.(10y – 8) + 3y = 7. (4)

Giải phương trình (4):

2.(10y – 8) + 3y = 7

20y – 16 + 3y = 7

23y = 23

y = 1.

Thay y = 1 vào phương trình (3), ta có:

x = 10.1 – 8 = 2.

Vậy hệ phương trình đã cho có nghiệm duy nhất (2; 1).

2. Phương pháp cộng đại số

Cách giải hệ phương trình bằng phương pháp cộng đại số:

Để giải một hệ hai phương trình bậc nhất hai ẩn có hệ số của cùng một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau, ta có thể làm như sau:

Bước 1. Cộng hay trừ từng vế của hai phương trình trong hệ để được phương trình chỉ còn chứa một ẩn.

Bước 2. Giải phương trình một ẩn vừa nhận được, từ đó suy ra nghiệm của hệ phương trình đã cho.

Chú ý: Trường hợp trong hệ phương trình đã cho không có hai hệ số của cùng một ẩn bằng nhau hay đối nhau, ta có thể đưa về trường hợp đã xét bằng cách nhân hai về của mỗi phương trình với một số thích hợp (khác 0).

Ví dụ 2. Giải hệ phương trình $\left\{\begin{array}{l}2x+3y=7\\ x-10y=-8\end{array}\right.$bằng phương pháp cộng đại số.

Hướng dẫn giải

Xét hệ phương trình $\left\{\begin{array}{l}2x+3y=7\left(1\right)\\ x-10y=-8\left(2\right)\end{array}\right.$

Nhân hai vế của phương trình (2) với 2, ta được hệ phương trình sau: $\left\{\begin{array}{l}2x+3y=7\left(3\right)\\ 2x-20y=-16\left(4\right)\end{array}\right.$

Trừ từng vế hai phương trình (3) và (4), ta nhận được phương trình:

23y = 23, tức là y = 1.

Thay y = 1 vào phương trình (2), ta có: x – 10.1 = –8. (5)

Giải phương trình (5):

x – 10.1 = –8

x – 10 = –8

x = 2.

Vậy hệ phương trình đã cho có nghiệm duy nhất (2; 1).

3. Sử dụng máy tính cầm tay để tìm nghiệm của hệ hai phương trình bậc nhất hai ẩn

Cách tìm nghiệm của hệ hai phương trình bậc nhất hai ẩn bằng máy tính cầm tay

Muốn tìm nghiệm của hệ hai phương trình bậc nhất hai ẩn bằng máy tính cầm tay (MTCT), chúng ta cần sử dụng loại máy có chức năng này (thường có phím MODE). Trước hết ta phải viết hệ phương trình cần tìm nghiệm dưới dạng: $\left\{\begin{array}{l}{a}_{1}x+b_{1}y=c_1\\ a_{2}x+b_{2}y=c_2.\end{array}\right.$

Chẳng hạn, để tìm nghiệm của hệ $\left\{\begin{array}{l}2x-3y-4=0\\ 5x-6y-7=0\end{array}\right.,$ ta viết nó dưới dạng $\left\{\begin{array}{l}2x-3y=4\\ 5x-6y=7\end{array}\right..$

Khi đó, ta có a₁ = 2, b₁ = 3, c₁ = 4; a₂ = 5, b₂ = 6 và c₂ = 7. Lần lượt thực hiện các bước sau (với máy tính thích hợp):

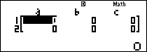
Bước 1. Vào chức năng giải hệ hai phương trình bậc nhất hai ẩn bằng cách bấm các phím (xem màn hình sau bước 1, con trỏ ở vị trí a₁).

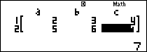
Bước 2. Nhập các số a₁ = 2, b₁ = 3, c₁ = 4; a₂ = 5, b₂ = 6 và c₂ = 7 bằng cách bấm: (xem màn hình sau bước 2).

Bước 3. Đọc kết quả: Sau khi kết thúc bước 2, bấm , màn hình cho x = –1; bấm tiếp phím , màn hình cho y = 2 (xem màn hình sau bước 3). Ta hiểu nghiệm của hệ phương trình là (–1; 2).

Màn hình sau bước 1

Màn hình sau bước 2

Màn hình sau bước 3

Chú ý:

– Muốn xóa số vừa nhập thì bấm phím muốn thay đổi số đã nhập ở một vị trí nào đó thì di chuyển con trỏ đến vị trí đó rồi nhập số mới.

– Bấm phím hay để chuyển đổi hiển thị các giá trị của x và y trong kết quả.

– Nếu máy báo “Infinite Sol” thì hệ phương trình đã cho có vô số nghiệm. Nếu máy báo “No-Solution” thì hệ phương trình đã cho vô nghiệm.

B. Bài tập Giải hệ hai phương trình bậc nhất hai ẩn

Bài 1. Khẳng định nào sau đây là đúng?

Hệ phương trình $\left\{\begin{array}{l}1,5x-0,6y=0,3\\ -2x+y=-2\end{array}\right.$

A. có nghiệm là (0; –0,5).

B. có nghiệm là (1; 0).

C. có nghiệm là (–3; –8).

D. vô nghiệm.

Hướng dẫn giải

Đáp án đúng là: C

Xét hệ phương trình $\left\{\begin{array}{l}1,5x-0,6y=0,3\left(1\right)\\ -2x+y=-2\left(2\right)\end{array}\right.$

Từ phương trình (2), ta có: y = 2x – 2. (*)

Thế vào phương trình (1) ta được: 1,5x – 0,6.(2x – 2) = 0,3. (**)

Giải phương trình (**):

1,5x – 0,6.(2x – 2) = 0,3

1,5x – 1,2x + 1,2 = 0,3

0,3x = –0,9

x = –3.

Thay x = –3 vào phương trình (*), ta có:

y = 2.(–3) – 2 = –8.

Vậy hệ phương trình đã cho có nghiệm duy nhất (–3; –8).

Bài 2. Giải các hệ phương trình sau bằng phương pháp thế:

a) $\left\{\begin{array}{l}x+y=5\\ 3x-2y=5.\end{array}\right.$

b) $\left\{\begin{array}{l}x+7y=14\\ 2x+14y=28.\end{array}\right.$

c) $\left\{\begin{array}{l}\frac{3}{2}x-2y=8\\ 3x-4y=11.\end{array}\right.$

Hướng dẫn giải

a) $\left\{\begin{array}{l}x+y=5\left(1\right)\\ 3x-2y=5\left(2\right).\end{array}\right.$

Từ phương trình (1), ta có: x = 5 – y. (*)

Thế vào phương trình (2) ta được: 3.(5 – y) – 2y = 5. (**)

Giải phương trình (**):

3.(5 – y) – 2y = 5

15 – 3y – 2y = 5

15 – 5y = 5

–5y = –10

y = 2.

Thay y = 2 vào phương trình (*), ta có:

x = 5 – 2 = 3.

Vậy hệ phương trình đã cho có nghiệm duy nhất (3; 2).

b) $\left\{\begin{array}{l}x+7y=14\left(3\right)\\ 2x+14y=28.\left(4\right)\end{array}\right.$

Từ phương trình (3), ta có: x = 14 – 7y. (***)

Thế vào phương trình (4) ta được: 2.(14 – 7y) + 14y = 28. (****)

Giải phương trình (****):

2.(14 – 7y) + 14y = 28

28 – 14y + 14y = 28

0y = 0.

Do đó phương trình (****) có vô số nghiệm.

Vậy hệ phương trình đã cho có vô số nghiệm.

c) $\left\{\begin{array}{l}\frac{3}{2}x-2y=8\left(5\right)\\ 3x-4y=11\left(6\right)\end{array}\right.$

Từ phương trình (5), ta có: $2y=\frac{3}{2}x-8,$ suy ra $y=\frac{3}{4}x-4.\left(7\right)$

Thế vào phương trình (6) ta được: $3x-4\cdot \left(\frac{3}{4}x-4\right)=11.\left(8\right)$

Giải phương trình (8):

$3x-4\cdot \left(\frac{3}{4}x-4\right)=11$

3x – 3x + 16 = 11

0x = –5.

Do đó phương trình (8) vô nghiệm.

Vậy hệ phương trình đã cho vô nghiệm.

Bài 3. Giải các hệ phương trình sau bằng phương pháp cộng đại số:

a) $\left\{\begin{array}{l}-0,5x+0,5y=1\\ -2x+2y=8.\end{array}\right.$

b) $\left\{\begin{array}{l}2x+6y=-7\\ 5x-2y=-9.\end{array}\right.$

c) $\left\{\begin{array}{l}3x-5y=2\\ -6x+10y=-4.\end{array}\right.$

Hướng dẫn giải:

a) $\left\{\begin{array}{l}-0,5x+0,5y=1\left(1a\right)\\ -2x+2y=8\left(2a\right)\end{array}\right.$

Nhân hai vế của phương trình (1a) với 4, ta được hệ phương trình sau: $\left\{\begin{array}{l}-2x+2y=4\left(3a\right)\\ -2x+2y=8\left(4a\right)\end{array}\right.$

Trừ từng vế hai phương trình (3a) và (4a), ta nhận được phương trình:

0x + 0y = 12.

Phương trình trên vô nghiệm.

Vậy hệ phương trình đã cho vô nghiệm.

b) $\left\{\begin{array}{l}2x+6y=-7\left(1b\right)\\ 5x-2y=-9\left(2b\right)\end{array}\right.$

Nhân hai vế của phương trình (2b) với 3, ta được hệ phương trình sau: $\left\{\begin{array}{l}2x+6y=-7\left(3b\right)\\ 15x-6y=-27\left(4b\right)\end{array}\right.$

Cộng từng vế hai phương trình (3b) và (4b), ta nhận được phương trình:

17x = –34, tức là x = –2.

Thay x = –2 vào phương trình (2b), ta có: 5.(–2) – 2y = –9. (5b)

Giải phương trình (5b):

5.(–2) – 2y = –9

–10 – 2y = –9

–2y = 1

$y=-\frac{1}{2}.$

Vậy hệ phương trình đã cho có nghiệm duy nhất $\left(-2;-\frac{1}{2}\right).$

c) $\left\{\begin{array}{l}3x-5y=2\left(1c\right)\\ -6x+10y=-4\left(2c\right)\end{array}\right.$

Nhân hai vế của phương trình (1c) với 2, ta được hệ phương trình sau: $\left\{\begin{array}{l}6x-10y=4\left(3c\right)\\ -6x+10y=-4\left(4c\right)\end{array}\right.$

Cộng từng vế hai phương trình (3c) và (4c), ta nhận được phương trình:

0x + 0y = 0.

Phương trình trên vô số nghiệm.

Vậy hệ phương trình đã cho có vô số nghiệm.

Bài 4. Khẳng định nào sau đây là đúng?

Hệ phương trình $\left\{\begin{array}{l}0,6x+0,3y=1,8\\ 2x+y=-6\end{array}\right.$

A. có một nghiệm.

B. vô nghiệm.

C. có vô số nghiệm.

D. có hai nghiệm.

Hướng dẫn giải

Đáp án đúng là: B

Xét hệ phương trình $\left\{\begin{array}{l}0,6x+0,3y=1,8\left(1\right)\\ 2x+y=-6\left(2\right)\end{array}\right.$

Từ phương trình (2), ta có: y = –6 – 2x. (*)

Thế vào phương trình (1) ta được: 0,6x + 0,3.(–6 – 2x) = 1,8. (**)

Giải phương trình (**):

0,6x + 0,3.(–6 – 2x) = 1,8

0,6x – 1,8 – 0,6x = 1,8

0x = 3,6.

Do đó phương trình (**) vô nghiệm.

Vậy hệ phương trình đã cho vô nghiệm.

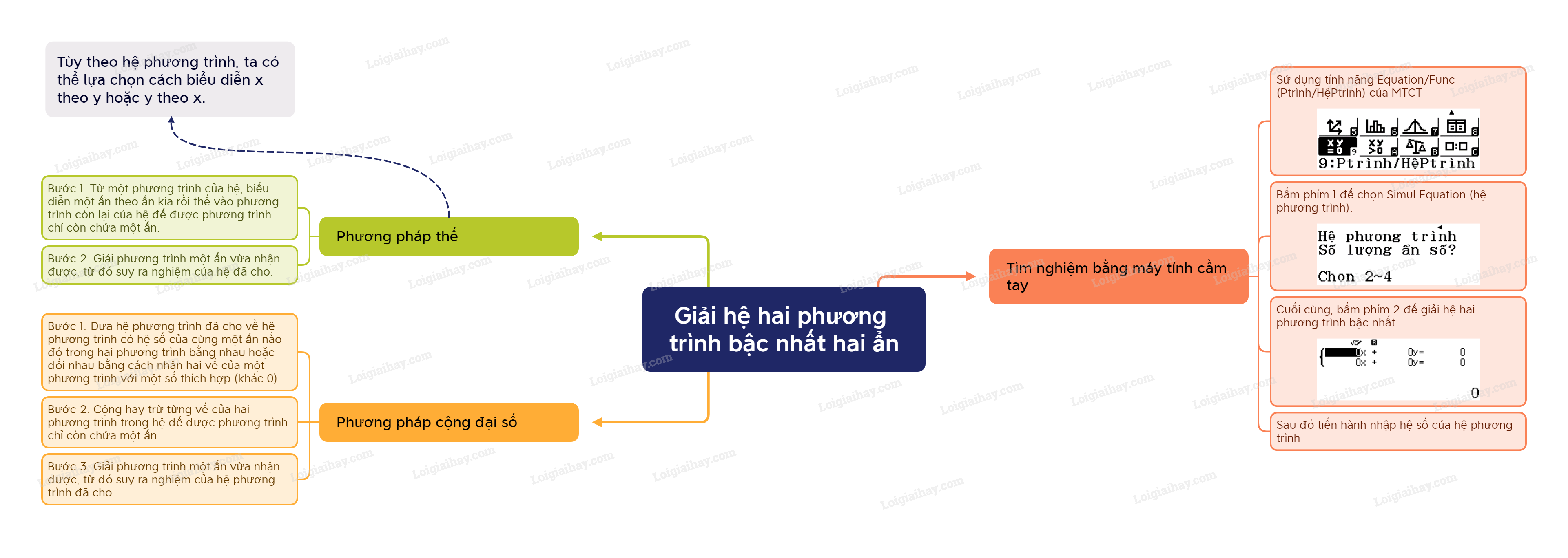
C. Sơ đồ tư duy Giải hệ hai phương trình bậc nhất hai ẩn