Lý thuyết Bất đẳng thức và tính chất – Toán lớp 9 Kết nối tri thức
Với lý thuyết Toán lớp 9 Bài 5: Bất đẳng thức và tính chất chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 9.
Lý thuyết Toán 9 Bài 5: Bất đẳng thức và tính chất - Kết nối tri thức
A. Lý thuyết Bất đẳng thức và tính chất
1. Bất đẳng thức
1.1. Nhắc lại thứ tự trên tập hợp số thực
– Trên tập số thực, với hai số a và b có ba trường hợp sau:
• Số a bằng số b, kí hiệu a = b;
• Số a lớn hơn số b, kí hiệu a > b;
• Số a nhỏ hơn số b, kí hiệu a < b.
Ví dụ 1.Thay trong các biểu thức sau bằng dấu thích hợp (=,>,<).
a)
b)
c)
Hướng dẫn giải
a)
b)
c)
– Khi biểu diễn số thực trên trục số, điểm biểu diễn số bé hơn nằm trước điểm biểu diễn số lớn hơn.
• Số a lớn hơn hoặc bằng số b, tức là a > b hoặc a = b, kí hiệu a ≥ b;
• Số a nhỏ hơn hoặc bằng số b, tức là a < b hoặc a = b, kí hiệu a ≤ b.
Ví dụ 2. Vì nên khi biểu diễn trên trục số thì điểm biểu diễn số nằm bên trái điểm biểu diễn số .
1.2. Khái niệm bất đẳng thức
Ta gọi hệ thức dạng a > b (hay a < b, a ≥ b, a ≤ b), được gọi là bất đẳng thức và a được gọi là vế trái, b được gọi là vế phải của bất đẳng thức.
Ví dụ 3. Xác định vế trái và vế phải của bất đẳng thức sau:
a) –6 < –4;
b) a2 + 5 ≥ 0.
Hướng dẫn giải
a) Vế trái là –6, vế phải là –4;
b) Vế trái là a2 + 5, vế phải là 0.
1.3. Tính chất bắc cầu
Bất đẳng thức có tính chất quan trọng sau:
Nếu a < b và b < c thì a < c (tính chất bắc cầu của bất đẳng thức).
Chú ý: Tương tự, các thứ tự lớn hơn (>), lớn hơn hoặc bằng (≥), nhỏ hơn hoặc bằng (≤) cũng có tính chất bắc cầu.
Ví dụ 4. Chứng minh
Hướng dẫn giải
Ta có ;
Do đó (điều phải chứng minh).
2. Liên hệ giữa thứ tự và phép cộng
Khi cộng cùng một số vào cả hai vế của một bất đẳng thức ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Với ba số a, b và c, ta có:
• Nếu a < b thì a + c < b + c.
• Nếu a ≤ b thì a + c ≤ b + c.
• Nếu a > b thì a + c > b + c.
• Nếu a ≥ b thì a + c ≥ b + c.
Ví dụ 5. Không thực hiện phép tính, hãy so sánh 2 025 + (–26) và 2 024 + (–26).
Hướng dẫn giải
Vì 2 025 > 2 024 nên
2 025 + (–26) > 2 024 + (–26). ← Cộng hai vế với cùng một số (–26).
3. Liên hệ giữa thứ tự và phép nhân
− Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương thì được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Với ba số a, b và c > 0, ta có:
• Nếu a < b thì ac < bc;
• Nếu a ≤ b thì ac ≤ bc;
• Nếu a > b thì ac > bc;
• Nếu a ≥ b thì ac ≥ bc.
− Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm thì được một bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.
Với ba số a, b và c > 0, ta có:
• Nếu a < b thì ac > bc;
• Nếu a ≤ b thì ac ≥ bc;
• Nếu a > b thì ac < bc;
• Nếu a ≥ b thì ac ≤ bc.
Ví dụ 6. Thay trong các biểu thức sau bởi dấu thích hợp (<, >) để được khẳng định đúng.
a)
b)
Hướng dẫn giải
a) Ta có –11,5 < 2,2 và 35 > 0 nên 35 . (–11,5) < 35 . 2,2.
Vậy
b) Ta có –11,5 < 2,2 và –35 < 0 nên (–35) . (–11,5) > (–35) . 2,2.
Vậy
B. Bài tập Bất đẳng thức và tính chất
Bài 1. Trên trục số, điểm biểu diễn số a nằm bên phải điểm biểu diễn số b. Khẳng định nào sau đây là đúng?
A. a < b.
B. a > b.
C. a ≤ b.
D. a = b.
Hướng dẫn giải
Đáp án đúng là: B
Vì trên trục số, điểm biểu diễn số a nằm bên phải điểm biểu diễn số b nên a lớn hơn b hay a > b.
Bài 2. Cho a > b. Khi đó ta có:
A. 2a > 7b.
B. 2a > 2b + 1.
C. 5a + 2 > 5b + 2.
D. –6a < –6b – 1.
Hướng dẫn giải
Đáp án đúng là: C
Ta có: a > b, suy ra 5a > 5b, do đó 5a + 2 > 5b + 2.
Bài 3. Xác định vế trái và vế phải của bất đẳng thức sau:
a) –3x + 2 > 7;
b) 2x – 1 ≤ 3x + 5;
c) x2 + 2 ≥ 0.
Hướng dẫn giải
a) Vế trái là –3x + 2, vế phải là 7;
b) Vế trái là 2x – 1, vế phải là 3x + 5;
c) Vế trái là x2 + 2, vế phải là 0.
Bài 4. Hãy cho biết các bất đẳng thức được tạo thành khi:
a) Cộng hai vế của bất đẳng thức a > 5 với −1;
b) Cộng hai vế của bất đẳng thức 2a – 1 ≤ b2 – 1 với 4;
c) Nhân hai vế của bất đẳng thức a < 3 với (–2), rồi tiếp tục cộng với 4;
Hướng dẫn giải
a) Cộng hai vế của bất đẳng thức a > 5 với −1 ta được:
a – 1 > 5 – 1
a – 1 > 4.
Vậy bất đẳng thức được tạo thành là a – 1 > 4.
b) Cộng hai vế của bất đẳng thức 2a – 1 ≤ b2 – 1 với 4 ta được:
2a – 1 + 4 ≤ b2 – 1 + 4
2a + 3 ≤ b2 + 3.
Vậy bất đẳng thức được tạo thành là 2a + 3 ≤ b2 + 3.
c) Nhân hai vế của bất đẳng thức a < 3 với (–2), rồi tiếp tục cộng với 4 ta được:
–2a > (–2) . 3
–2a + 4 > (–2) . 3 + 4
–2a + 4 > –2.
Vậy bất đẳng thức được tạo thành là –2a + 4 > –2.
Bài 5. Cho m > n, hãy so sánh:
a) 4m +5 và 4n +5;
b) –2m –11 và –2n –11.
Lời giải:
a) Vì m > n nên 4a >4b, suy ra 4m +5 > 4n +5.
Vậy 4m +5 > 4n +5.
b) Vì m > n nên –2m < –2n, suy ra –2m –11 và –2n –11.
Vậy –2m –11 và –2n –11.
Bài 6. Hệ thức nào sau đây là bất đẳng thức?
A. 2x – 8 = 0.
B. 3x = y.
C. 3x2 + 1 = 0.
D. y2 – 2 ≥ 0.
Hướng dẫn giải
Đáp án đúng là: D
• Các hệ thức 2x – 8 = 0; 3x2 + 1 = 0; 3x = y là đẳng thức.
• Hệ thức y2 – 2 ≥ 0 là bất đẳng thức.
C. Sơ đồ tư duy Bất đẳng thức và tính chất
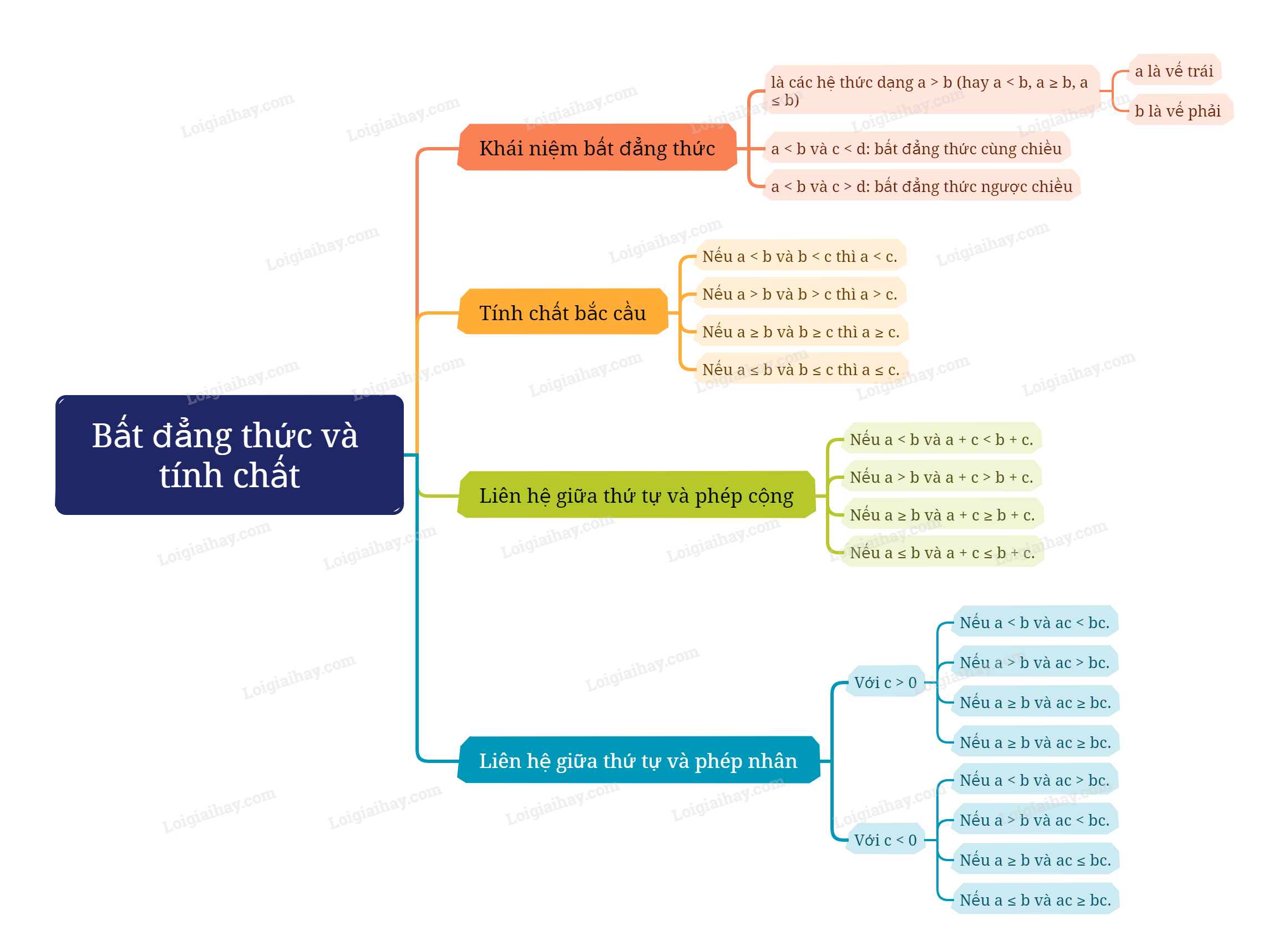
Xem thêm các chương trình khác:
- Soạn văn 9 Kết nối tri thức (hay nhất)
- Văn mẫu 9 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 9 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 9 - Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 9 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn 9 – Kết nối tri thức
- Soạn văn 9 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 9 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 9 - Global success
- Trọn bộ Từ vựng Tiếng Anh 9 Global success đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 9 Global success đầy đủ nhất
- Giải sbt Tiếng Anh 9 – Global Success
- Giải sgk Khoa học tự nhiên 9 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sgk Lịch sử 9 – Kết nối tri thức
- Giải sbt Lịch sử 9 – Kết nối tri thức
- Giải sgk Địa lí 9 – Kết nối tri thức
- Giải sbt Địa lí 9 – Kết nối tri thức
- Giải sgk Tin học 9 – Kết nối tri thức
- Giải sbt Tin học 9 – Kết nối tri thức
- Giải sgk Công nghệ 9 – Kết nối tri thức
- Giải sgk Giáo dục công dân 9 – Kết nối tri thức
- Giải sbt Giáo dục công dân 9 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 9 – Kết nối tri thức

