Lý thuyết Giải bài toán bằng cách lập hệ phương trình Toán lớp 9 (Kết nối tri thức)

Lý thuyết Toán 9 Bài 3: Giải bài toán bằng cách lập hệ phương trình - Kết nối tri thức

A. Lý thuyết Giải bài toán bằng cách lập hệ phương trình

Các bước giải một bài toán bằng cách lập hệ phương trình:

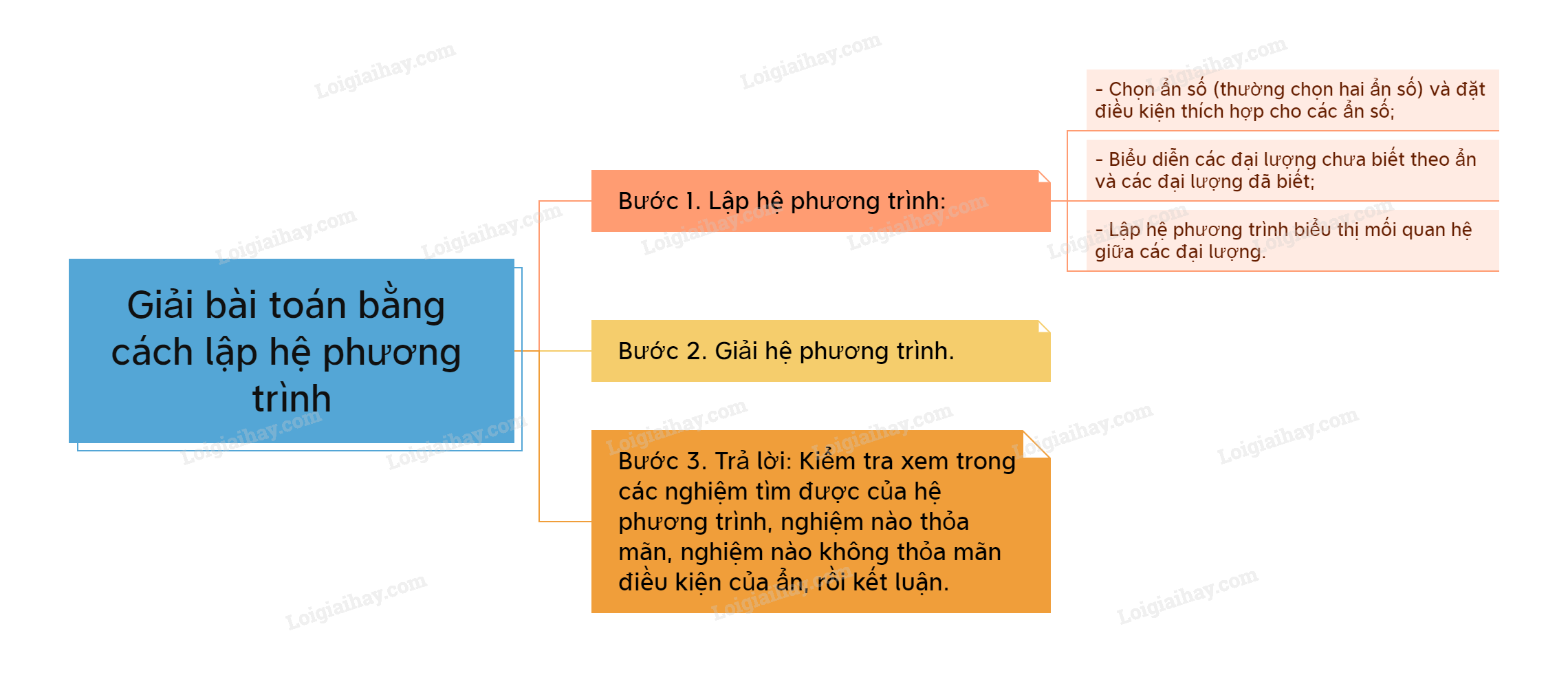
Bước 1. Lập hệ phương trình:

– Chọn ẩn số (thường chọn hai ẩn số) và đặt điều kiện thích hợp cho các ẩn số;

– Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết;

Bước 2. Giải hệ phương trình.

Bước 3. Trả lời: Kiểm tra xem trong các nghiệm tìm được của hệ phương trình, nghiệm nào thỏa mãn, nghiệm nào không thỏa mãn điều kiện của ẩn, rồi kết luận.

Ví dụ: Bác Phương chia số tiền 800 triệu đồng của mình cho hai khoản đầu tư. Sau một năm, tổng số tiền lãi thu được là 54 triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là 6%/năm và khoản đầu tư thứ hai là 8%/năm. Tính số tiền bác Phương đầu tư cho mỗi khoản.

Hướng dẫn giải

⦁ Gọi số tiền bác Phương đã đầu tư cho khoản thứ nhất và thứ hai lần lượt là x, y (triệu đồng) (0 < x < 800, 0 < y < 800).

Theo bài, tổng số tiền cho hai khoản đầu tư là 800 triệu đồng nên ta có phương trình:

x + y = 800.

Số tiền lãi thu được mỗi năm từ khoản đầu tư thứ nhất là x.6% = 0,06x (triệu đồng).

Số tiền lãi thu được mỗi năm từ khoản đầu tư thứ hai là x.8% = 0,08y (triệu đồng).

Theo bài, tổng số tiền lãi thu được là 54 triệu đồng nên ta có phương trình:

0,06x + 0,08y = 54, hay 3x + 4y = 2 700.

Ta có hệ phương trình: $\left\{\begin{array}{l}x+y=800\\ 3x+4y=2700.\end{array}\right.$

⦁ Giải hệ phương trình: $\left\{\begin{array}{l}x+y=800\\ 3x+4y=2700.\end{array}\right.$

Nhân hai vế của phương trình thứ nhất với 4, ta được hệ phương trình sau: $\left\{\begin{array}{l}4x+4y=3200\\ 3x+4y=2700.\end{array}\right.$

Trừ hai vế của hai phương trình trên, ta nhận được: x = 500.

Thay x = 500 vào phương trình x + y = 800, ta có 500 + y = 800. (1)

Giải phương trình (1):

500 + y = 800

y = 300.

⦁ Các giá trị tìm được của x và y thỏa mãn điều kiện của ẩn.

Trả lời: Số tiền bác Phương đã đầu tư cho khoản thứ nhất là 500 triệu đồng và cho khoản thứ hai là 300 triệu đồng.

B. Bài tập Giải bài toán bằng cách lập hệ phương trình

Bài 1. Hai người thợ cùng làm công việc trong 16 giờ thì xong. Nếu người thứ nhất làm một mình trong 15 giờ rồi người thứ hai làm tiếp 6 giờ thì hoàn thành được 75% công việc. Hỏi mỗi người làm công việc đó một mình hoàn thành trong bao lâu?

Hướng dẫn giải

– Gọi x là số giờ để người thứ nhất hoàn thành công việc nếu làm một mình; y là số giờ để người thứ hai hoàn thành công việc nếu làm một mình. Điều kiện: x > 0 và y > 0.

Mỗi giờ người thứ nhất làm được $\frac{1}{x}$ (công việc) và người thứ hai làm được $\frac{1}{y}$ (công việc).

Hai người cùng làm công việc trong 16 giờ thì xong nên mỗi giờ, hai người làm chung thì được $\frac{1}{16}$ (công việc). Ta có phương trình: $\frac{1}{x}+\frac{1}{y}=\frac{1}{16}.\left(1\right)$

Người thứ nhất làm một mình trong 15 giờ thì được $15\cdot \frac{1}{x}=\frac{15}{x}$ (công việc).

Người thứ hai làm một mình trong 6 giờ thì được $6\cdot \frac{1}{y}=\frac{6}{y}$ (công việc).

Nếu người thứ nhất làm một mình trong 15 giờ rồi người thứ hai làm tiếp 6 giờ thì hoàn thành được 75% công việc nên ta có phương trình: $\frac{15}{x}+\frac{6}{y}=75\%=\frac{3}{4}.\left(2\right)$

Từ (1) và (2) ta có hệ phương trình: $\left(I\right)\left\{\begin{array}{l}\frac{1}{x}+\frac{1}{y}=\frac{1}{16}\\ \frac{15}{x}+\frac{6}{y}=\frac{3}{4}.\end{array}\right.$

Nếu đặt $u=\frac{1}{x}$ và $v=\frac{1}{y}$ thì ta có hệ phương trình bậc nhất hai ẩn mới là u và v như sau: $\left(II\right)\left\{\begin{array}{l}u+v=\frac{1}{16}\left(3\right)\\ 15u+6v=\frac{3}{4}\left(4\right)\end{array}\right.$

Giải hệ (II):

Nhân hai vế của phương trình (3) với 6, ta được hệ $\left\{\begin{array}{l}6u+6v=\frac{6}{16}\\ 15u+6v=\frac{3}{4}\end{array}\right.$ hay $\left\{\begin{array}{l}6u+6v=\frac{3}{8}\\ 15u+6v=\frac{3}{4}.\end{array}\right.$

Trừ từng vế hai phương trình của hệ trên, ta được: $\left(6u-15u\right)+\left(6v-6v\right)=\frac{3}{8}-\frac{3}{4}$ hay $-9u=-\frac{3}{8},$ suy ra $u=\frac{1}{24}.$

Thay $u=\frac{1}{24}$ vào phương trình (3), ta được: $\frac{1}{24}+v=\frac{1}{16},$ suy ra $v=\frac{1}{16}-\frac{1}{24}=\frac{1}{48}.$

Từ đó, ta có:

⦁ $u=\frac{1}{x}=\frac{1}{24},$ suy ra x = 24;

⦁ $v=\frac{1}{y}=\frac{1}{48},$ suy ra y = 48.

– Các giá trị tìm được của x và y thỏa mãn điều kiện của ẩn.

Trả lời: Nếu làm một mình thì người thứ nhất làm xong công việc trong 24 giờ, còn người thứ hai làm xong trong 48 giờ.

Bài 2. Nhân dịp ngày Giỗ Tổ Hùng Vương, một siêu thị điện máy đã giảm giá nhiều mặt hàng để kích cầu mua sắm. Giá niêm yết của một chiếc tủ lạnh và một chiếc máy giặt có tổng số tiền là 25,4 triệu đồng. Tuy nhiên, trong dịp này tủ lạnh giảm 40% giá niêm yết và máy giặt giảm 25% giá niêm yết. Vì thế, cô Ngọc đã mua hai mặt hàng trên với tổng số tiền là 16,77 triệu đồng. Hỏi giá niêm yết của mỗi mặt hàng trên là bao nhiêu?

Hướng dẫn giải

⦁ Gọi giá niêm yết của một chiếc tủ lạnh và một chiếc máy giặt lần lượt là x, y (triệu đồng) (0 < x < 25,4; 0 < y < 25,4).

Theo bài, giá niêm yết của một chiếc tủ lạnh và một chiếc máy giặt có tổng số tiền là 25,4 triệu đồng nên ta có: x + y = 25,4.

Do tủ lạnh được giảm 40% giá niêm yết nên giá của chiếc tủ lạnh sau giảm giá là x.(100% – 40%) = x.60% = 0,6x (triệu đồng).

Do máy giặt được giảm 25% giá niêm yết nên giá của chiếc máy lạnh sau giảm giá là y.(100% – 25%) = y.75% = 0,75y (triệu đồng).

Theo bài, cô Ngọc đã mua hai mặt hàng trên với tổng số tiền là 16,77 triệu đồng nên ta có phương trình: 0,6x + 0,75y = 16,77 hay 60x + 75y = 1 677.

Ta có hệ phương trình: $\left\{\begin{array}{l}x+y=25,4\\ 60x+75y=1677.\end{array}\right.$

⦁ Giải hệ phương trình $\left\{\begin{array}{l}x+y=25,4\\ 60x+75y=1677.\end{array}\right.$

Nhân hai vế của phương trình thứ nhất với 75, ta nhận được hệ phương trình sau:

$\left\{\begin{array}{l}75x+75y=1905\\ 60x+75y=1677.\end{array}\right.$

Trừ hai vế của phương trình thứ nhất cho phương trình thứ hai của hệ phương trình trên, ta có: 15x = 228. (1)

Giải phương trình (1):

15x = 228

x = 15,2.

Thay x = 15,2 vào phương trình x + y = 25,4, ta được: 15,2 + y = 25,4. (2)

Giải phương trình (2):

15,2 + y = 25,4

y = 10,2.

⦁ Các giá trị tìm được của x và y thỏa mãn điều kiện của ẩn.

Trả lời: Giá niêm yết của một chiếc tủ lạnh là 15,2 triệu đồng và giá niêm yết của một chiếc máy giặt là 10,2 triệu đồng.

C. Sơ đồ tư duy Giải bài toán bằng cách lập hệ phương trình