Lý thuyết Hàm số y = ax^2 (a ≠ 0) - Toán 9 Kết nối tri thức

Lý thuyết Toán 9 Bài 18: Hàm số y = ax² (a ≠ 0)

1. Hàm số y = ax² (a ≠ 0)

Nhận biết hàm số y = ax² (a ≠ 0)

Ví dụ 1.

– Khi thả một vật rơi tự do và bỏ qua sức cản của không khí, quãng đường chuyển động s (mét) của vật được cho bằng công thức s = 4,9t², trong đó t (giây) là thời gian chuyển động của vật.

– Công thức tính diện tích S của hình tròn bán kính r là: S = π.r².

Những công thức tính s theo t, tính S theo r trong Ví dụ 1 biểu thị những hàm số có cùng một dạng, gọi là hàm số y = ax² (a ≠ 0).

Nhận xét: Hàm số y = ax² (a ≠ 0) xác định với mọi giá trị x thuộc ℝ.

Ví dụ 2. Hoàn thành bảng giá trị sau của hàm số y = –4x²:

x	–3	–2	–1	0	1	2	3
y = –4x2	?	?	?	?	?	?	?

Hướng dẫn giải

Thay x = –3 vào hàm số y = –4x², ta có y = –4.(–3)² = –36.

Tương tự, ta thay lần lượt các giá trị x = –2; x = –1; x = 0; x = 1; x = 2; x = 3 vào hàm số y = –4x², ta hoàn thành được bảng sau:

x	–3	–2	–1	0	1	2	3
y = –4x2	–36	–16	–4	0	–4	–16	–36

2. Đồ thị của hàm số y = ax² (a ≠ 0)

2.1. Cách vẽ đồ thị hàm số y = ax² (a ≠ 0)

Bước 1. Lập bảng ghi một số cặp giá trị tương ứng của x và y.

Bước 2. Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số y = ax² (a ≠ 0).

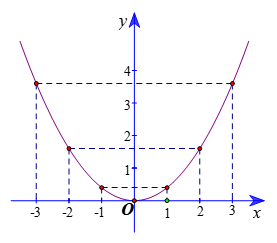
Ví dụ 3. Vẽ đồ thị của hàm số $y=\frac{2}{5}{x}^2.$

Hướng dẫn giải

Lập bảng một số giá trị tương ứng của x và y:

Biểu diễn các điểm $\left(-3;\frac{18}{5}\right),$$\left(-2;\frac{8}{5}\right),$$\left(-1;\frac{2}{5}\right),$$\left(0;0\right),$$\left(1;\frac{2}{5}\right),$$\left(2;\frac{8}{5}\right),$$\left(3;\frac{18}{5}\right)$trên mặt phẳng tọa độ Oxy và nối chúng lại, ta được đồ thị hàm số $y=\frac{2}{5}{x}^2$như hình vẽ dưới.

2.2. Nhận biết tính đối xứng của đồ thị hàm số y = ax² (a ≠ 0)

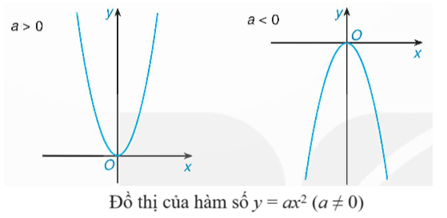
Đồ thị của hàm số y = ax² (a ≠ 0) là một đường cong, gọi là đường parabol, có các tính chất sau:

⦁ Có đỉnh là gốc tọa độ O;

⦁ Có trục đối xứng là Oy;

⦁ Nằm phía trên trục hoành nếu a > 0 và nằm phía dưới trục hoành nếu a < 0.

Chú ý: Hai điểm (x; y) và (–x; y) đối xứng nhau qua trục tung Oy.

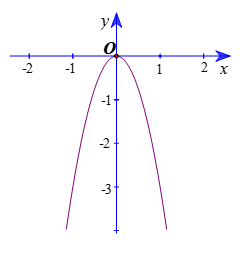
Ví dụ 4. Cho hàm số y = –3x² có đồ thị là parabol như hình vẽ.

a) Hai điểm A(1; –3) và B(–1; –3) có thuộc parabol đã cho không?

b) Nhận xét về tính đối xứng giữa hai điểm A và B.

Hướng dẫn giải

a) Ta có: –3 = 3.1² (đúng). Suy ra A(1; –3) thuộc parabol đã cho.

Tương tự, ta có: –3 = 3.(–1)² (đúng). Suy ra B(–1; –3) thuộc parabol đã cho.

Vậy hai điểm A(1; –3) và B(–1; –3) thuộc parabol đã cho.

b) Hai điểm A(1; –3) và B(–1; –3) đối xứng với nhau qua trục tung Oy.

Nhận xét:

⦁ Khi vẽ đồ thị hàm số y = ax² (a ≠ 0), ta cần xác định tối thiểu 5 điểm thuộc đồ thị là gốc tọa độ O và hai cặp điểm đối xứng với nhau qua trục tung Oy.

⦁ Do đồ thị của hàm số y = ax² (a ≠ 0) nhận trục tung Oy là trục đối xứng nên ta có thể lập bảng giá trị của hàm số này với những giá trị x không âm và vẽ phần đồ thị tương ứng ở bên phải trục tung, sau đó lấy đối xứng phần đồ thị đã vẽ qua trục tung ta sẽ được đồ thị của hàm số đã cho.

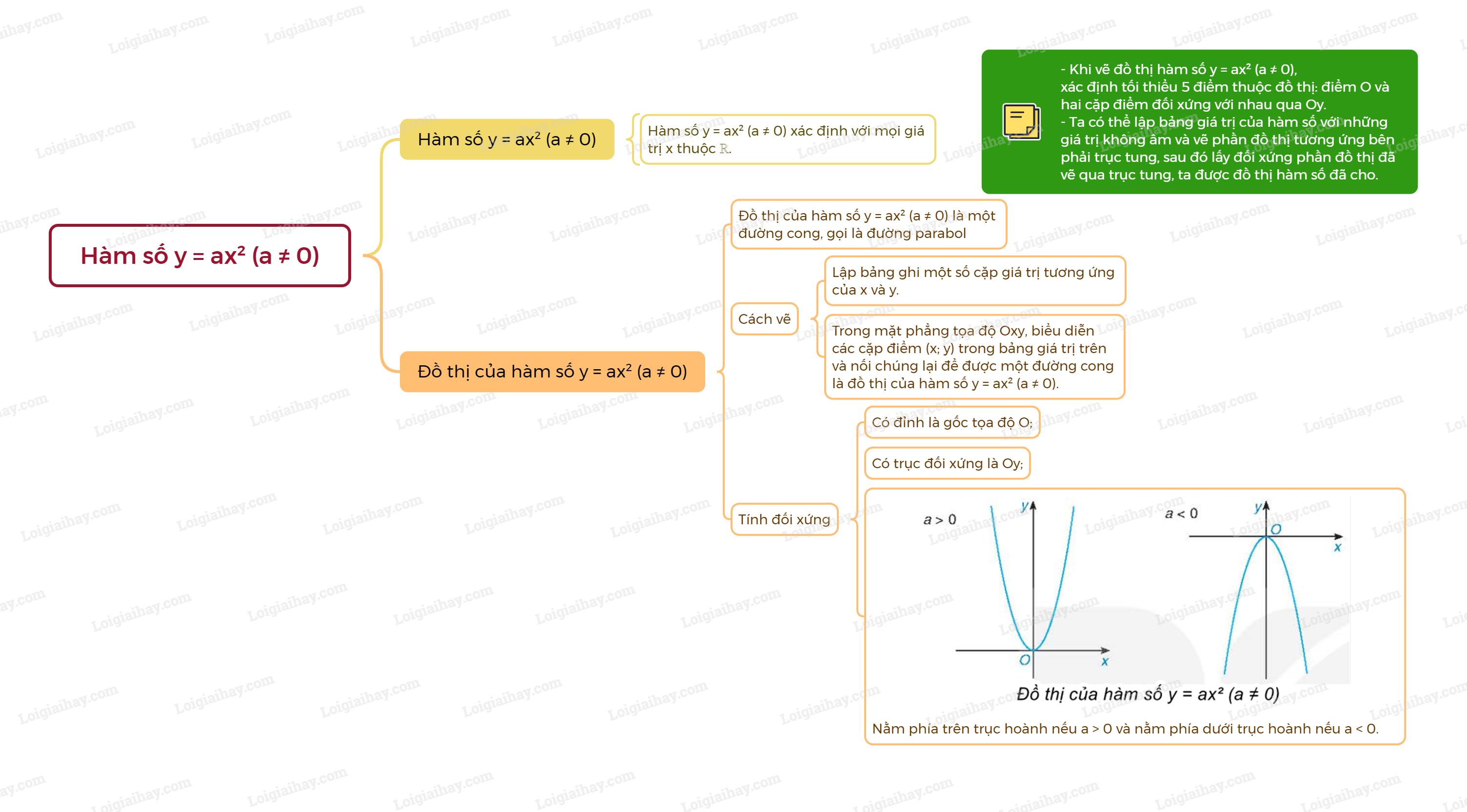
Sơ đồ tư duy Hàm số y = ax² (a ≠ 0)

Bài tập Hàm số y = ax² (a ≠ 0)

Bài 1. Hàm số nào sau đây có dạng y = ax² (a ≠ 0)?

A. y = –6x;

B. y = x²;

C. y = 0x²;

D. $y=\frac{2}{x^2}.$

Hướng dẫn giải

Đáp án đúng là: B

Hàm số y = x² có dạng y = ax² (a ≠ 0) với a = 1.

Các hàm số y = –6x; y = 0x² và $y=\frac{2}{x^2}$ không có dạng y = ax² (a ≠ 0).

Vậy ta chọn phương án B.

Bài 2. Đồ thị của hàm số y = ax² (a ≠ 0) là một đường cong nằm phía trên trục hoành nếu

A. a > 0;

B. a < 0;

C. a = 1;

D. a = –2.

Hướng dẫn giải

Đáp án đúng là: A

Đồ thị của hàm số y = ax² (a ≠ 0) là một đường cong, gọi là parabol, nằm phía trên trục hoành nếu a > 0.

Vậy ta chọn phương án A.

Bài 3. Cho điểm M(–4; 7) thuộc đồ thị hàm số y = ax² (a ≠ 0). Điểm đối xứng của M(–4; 8) qua trục đối xứng của đồ thị hàm số đã cho là

A. N(4; –7);

B. P(–4; –7);

C. M(–4; 7);

D. Q(4; 7).

Hướng dẫn giải

Đáp án đúng là: D

Ta có trục đối xứng của đồ thị hàm số đã cho là trục tung Oy.

Suy ra điểm đối xứng của M(–4; 7) qua trục tung Oy là Q(4; 7).

Vậy ta chọn phương án D.

Bài 4. Cho hàm số y = –2x².

a) Trong các điểm A(4; –32), B(–8; –86), $C\left(\frac{3}{4};-\frac{9}{8}\right),$ điểm nào thuộc đồ thị hàm số?

b) Tìm các điểm thuộc đồ thị của hàm số có hoành độ lần lượt bằng 2 và –5.

c) Tìm các điểm thuộc đồ thị của hàm số có tung độ bằng –98.

Hướng dẫn giải

a) Ta có: –32 = –2.4² (đúng). Suy ra điểm A(4; –32) thuộc đồ thị hàm số.

Ta có: –2.(–8)² = –128 ≠ –86 (sai). Suy ra điểm B(–8; –86) không thuộc đồ thị hàm số.

Ta có: $-\frac{9}{8}=-2.{\left(\frac{3}{4}\right)}^2$ (đúng). Suy ra điểm $C\left(\frac{3}{4};-\frac{9}{8}\right)$ thuộc đồ thị hàm số.

Vậy điểm A(4; –32) và điểm $C\left(\frac{3}{4};-\frac{9}{8}\right)$ thuộc đồ thị hàm số y = –2x²; điểm B(–8; –86) không thuộc đồ thị hàm số y = –2x².

b) Với x = 2, ta có: y = –2.2² = –8.Suy ra tọa độ M(2; –8).

Với x = –5, ta có: y = –2.(–5)² = –50. Suy ra tọa độ N(–5; –50).

Vậy tọa độ M(2; –8) và N(–5; –50) thỏa mãn yêu cầu bài toán.

c) Với y = –98, ta có: –2x² = –98, hay x² = 49.

Suy ra x = 7 hoặc x = –7.

Vậy tọa độ P(7; –98) và Q(–7; –98) thỏa mãn yêu cầu bài toán.

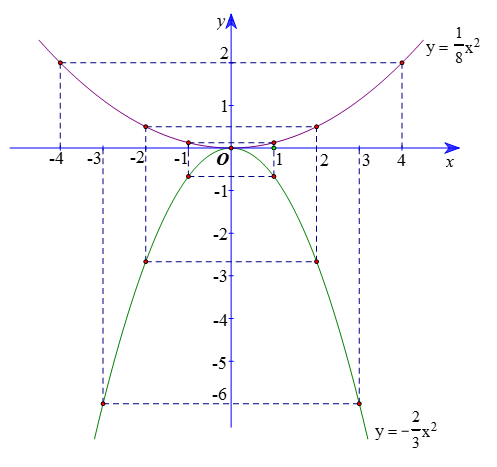
Bài 5. Cho hai hàm số $y=\frac{1}{8}{x}^2$ và $y=-\frac{2}{3}{x}^2.$ Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng tọa độ Oxy.

Hướng dẫn giải

⦁ Lập bảng một số giá trị tương ứng giữa x và y của hàm số $y=\frac{1}{8}{x}^2:$

Biểu diễn các điểm (–4; 2), $\left(-2;\frac{1}{2}\right),$ $\left(-1;\frac{1}{8}\right),$ (0; 0), $\left(1;\frac{1}{8}\right),$ $\left(2;\frac{1}{2}\right),$ (4; 2) trên mặt phẳng tọa độ Oxy và nối chúng lại, ta được đồ thị hàm số $y=\frac{1}{8}{x}^2.$

⦁ Lập bảng một số giá trị tương ứng giữa x và y của hàm số $y=-\frac{2}{3}{x}^2:$

Biểu diễn các điểm (–3; –6), $\left(-2;-\frac{8}{3}\right),$ $\left(-1;-\frac{2}{3}\right),$ (0; 0), $\left(1;-\frac{2}{3}\right),$ $\left(2;-\frac{8}{3}\right),$ (3; –6) trên mặt phẳng tọa độ Oxy và nối chúng lại, ta được đồ thị hàm số $y=-\frac{2}{3}{x}^2.$

Bài 6. Lực F (N) của gió khi thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương tốc độ v (m/s) của gió theo công thức: F = av², ở đó a là một hằng số và a ≠ 0. Biết rằng khi tốc độ gió là 3 m/s thì lực tác động lên cánh buồm của con thuyền bằng 405 N.

a) Tính hằng số a.

b) Khi tốc độ của gió là v = 12 m/s thì lực F của gió tác động lên cánh buồm là bao nhiêu?

c) Cánh buồm của thuyền chỉ chịu được lực tác động tối đa là 15 000 N. Hỏi con thuyền có thể ra khơi khi tốc độ của gió là 72 km/h hay không? Vì sao?

Hướng dẫn giải

a) Thay v = 3, F = 405 vào công thức F = av², ta được:

405 = a.3² hay 9a = 405.Suy ra a = 45 (thỏa mãn).

Vậy a = 45.

b) Vì a = 45 nên F = 45v².

Với v = 12, ta có: F = 45.12² = 6480 (N).

Vậy khi tốc độ của gió là v = 12 m/s thì lực F của gió tác động lên cánh buồm là 6 480 N.

c) Đổi 72 km/h = 20 m/s.

Với v = 20 m/s, ta có: F = 45.20² = 18 000 (N).

Vì 18 000 > 15 000 nên con thuyền không thể ra khơi khi tốc độ gió là 72 km/h.