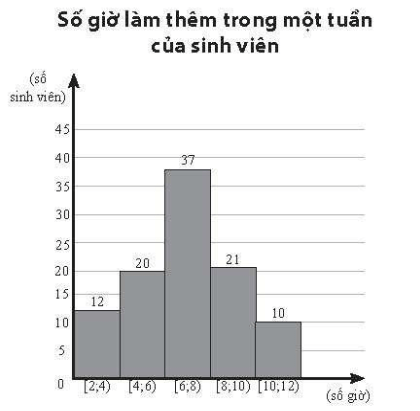
Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được cho ở biểu đồ bên

Lời giải Bài 5 trang 162 SBT Toán 11 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

1 293 05/11/2023

Trang trước

Trang sau

Giải SBT Toán 11 Bài tập cuối chương 5 trang 160

Bài 5 trang 162 SBT Toán 11 Tập 1: Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được cho ở biểu đồ bên.

Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được

Hãy ước lượng số trung bình, mốt và các tứ phân vị của số liệu đó.

Lời giải:

Từ mẫu số liệu ghép nhóm, ta có bảng thống kê số giờ làm thêm trong một tuần của 100 sinh viên như sau:

Số giờ làm thêm	[2; 4)	[4; 6)	[6; 8)	[8; 10)	[10; 12)
Số giờ làm thêm đại diện	3	5	7	9	11
Số sinh viên	12	20	37	21	10

Cỡ mẫu n = 100.

Số trung bình của mẫu số liệu ghép nhóm trên là

$\bar{x} = \frac{3 \cdot 12 + 5 \cdot 20 + 7 \cdot 37 + 9 \cdot 21 + 11 \cdot 10}{100}$ = 6,94.

Nhóm chứa mốt của mẫu số liệu trên là nhóm [6; 8).

Do đó: u_m = 6; n_m = 37; n_{m ‒ 1} = 20; n_{m + 1} = 21; u_{m + 1} =8.

Vậy mốt của mẫu số liệu ghép nhóm là

$M_{O} = 6 + \frac{37 - 20}{(37 - 20) + (37 - 21)} \cdot (8 - 6) = \frac{232}{33} \approx 7, 03$ .

Gọi x₁; x₂; ...; x₁₀₀ là mẫu số liệu được xếp theo thứ tự không giảm.

Tứ phân vị thứ hai của mẫu số liệu x₁; x₂; ...; x₁₀₀ là $\frac{1}{2} (x_{50} + x_{51})$ . Do x₅₀ và x₅₁ thuộc nhóm [6; 8) nên tứ phân vị thứ hai của mẫu số liệu là

$Q_{2} = 6 + \frac{\frac{100}{2} - (12 + 20)}{37} \cdot (8 - 6) = \frac{258}{37} \approx 6, 97$ .

Tứ phân vị thứ nhất của dãy số liệu x₁; x₂; ...; x₁₀₀ là $\frac{1}{2} (x_{25} + x_{26})$ . Do x₂₅ và x₂₆ thuộc nhóm [4; 6) nên tứ phân vị thứ nhất của mẫu số liệu là

$Q_{1} = 4 + \frac{\frac{100}{4} - (12 + 0)}{20} \cdot (6 - 4)$ = 5,3.

Tứ phân vị thứ ba của dãy số liệu x₁; x₂; ...; x₁₀₀ là $\frac{1}{2} (x_{75} + x_{76})$ . Do x₇₅ và x₇₆ thuộc nhóm [8; 10) nên tứ phân vị thứ ba của mẫu số liệu là