Nội dung bài viết

    Xem thêm

    Giải SBT Toán 7 trang 24 Tập 1 Kết nối tri thức

    Với Giải SBT Toán 7 trang 24 Tập 1 trong Bài 5: Làm quen với số thập phân vô hạn tuần hoàn Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 24.

    1 582 30/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 7 trang 24 Tập 1 Kết nối tri thức

    Bài 2.1 trang 24 SBT Toán 7 Tập 1: Trong các phân số sau, phân số nào viết được dưới dạng số thập phân vô hạn tuần hoàn? Vì sao?

    2160;−8125;28−63;37800

    Lời giải:

    *) 2160

    Ta có:

    2160=21:360:3=720.

    Mẫu số: 20 = 2.2.5 nên 20 chỉ có ước nguyên tố là 2 và 5.

    Do đó, phân số 720 hay 2160 viết được dưới dạng số thập phân hữu hạn.

    *) −8125

    Mẫu số 125 = 53 nên 125 chỉ có ước nguyên tố là 5.

    Do đó, phân số −8125 viết được dưới dạng số thập phân hữu hạn.

    *) 28−63

    Ta có:

    28−63=28:(−7)(−63):(−7)=−49

    Mẫu số 9 = 3.3 nên 9 có ước nguyên tố là 3.

    Do đó, phân số −49 hay 28−63 viết được dưới dạng số thập phân vô hạn tuần hoàn.

    *) 37800

    Mẫu số 800 = 25.52 nên 800 chỉ có ước nguyên tố là 2 và 5.

    Do đó, phân số 37800 viết được dưới dạng số thập phân hữu hạn.

    Vậy phân số viết được thành số thập phân vô hạn tuấn hoàn là 28−63.

    Bài 2.2 trang 24 SBT Toán 7 Tập 1: Viết số thập phân 2,75 dưới dạng phân số tối giản.

    Lời giải:

    Ta có:

    2,75 = 275100=275:25100:25=74.

    Số thập phân 2,75 được viết dưới dạng phân số tối giản là 74

    Bài 2.3 trang 24 SBT Toán 7 Tập 1: Nỗi mỗi phân số ở cột bên trái với cách viết thập phân của nói ở cột bên phải:

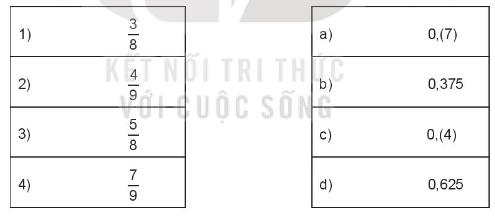
    Sách bài tập Toán 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn - Kết nối tri thức (ảnh 1)

    Lời giải:

    Ta có:

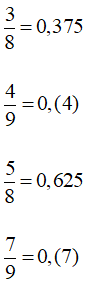
    Sách bài tập Toán 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn - Kết nối tri thức (ảnh 1)

    Ta có kết quả nối sau:

    1 – b

    2 – c

    3 – d

    4 – a

    Bài 2.4 trang 24 SBT Toán 7 Tập 1: Trong các phân số: 1315;134; −118;116;720;−1950, gọi A là tập hợp các phân số được viết thành số thập phân hữu hạn và B là tập hợp các phân số viết được thành số thập phân vô hạn tuần hoàn. Liệt kê và viết các phần tử của hai tập hợp theo thứ tự từ nhỏ đến lớn.

    Lời giải:

    1315 mẫu số là 15 có ước nguyên tố là 3 và 5 nên phân số được viết dưới dạng số thập phân vô hạn tuần hoàn.

    134 mẫu số là 4 có ước nguyên tố là 2 nên phân số được viết dưới dạng số thập phân hữu hạn.

    -118 mẫu số là 18 có ước nguyên tố là 3 và 2 nên phân số được viết dưới dạng số thập phân vô hạn tuần hoàn.

    116 mẫu số là 6 có ước nguyên tố là 2 và 3 nên phân số được viết dưới dạng số thập phân vô hạn tuần hoàn.

    720 mẫu số là 20 có ước nguyên tố là 2 và 5 nên phân số được viết dưới dạng số thập phân hữu hạn.

    -1950 mẫu số là 50 có ước nguyên tố là 2 và 5 nên phân số được viết dưới dạng số thập phân hữu hạn.

    Các phần tử của tập hợp A là 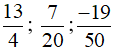Sách bài tập Toán 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn - Kết nối tri thức (ảnh 1)

    Các phần tử của tập hợp B là 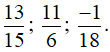Sách bài tập Toán 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn - Kết nối tri thức (ảnh 1)

    + Ta đi so sánh các phần tử của tập hợp A.

    −1950 là phân số âm và 134; 720 là phân số dương nên -1950 bé nhất.

    Lại có 134 là phân số dương có tử số lớn hơn mẫu số nên 134 > 1

    720 là phân số dương có tử số bé hơn mẫu số nên 720 < 1.

    Tập hợp A gồn các phân số được viết thành số thập phân hữu hạn, khi liệt kê và viết các phần tử theo thứ tự từ bé đến lớn là:

    A=−1950;720;134

    + Ta đi so sánh các phần tử của tập hợp B.

    −118 là phân số âm và 1315; 116 là phân số dương nên −118 bé nhất.

    Lại có 116 là phân số dương có tử số lớn hơn mẫu số nên 116 > 1

    1315 là phân số dương có tử số bé hơn mẫu số nên 1315 < 1.

    Tập hợp B gồn các phân số được viết thành số thập phân hữu hạn, khi liệt kê và viết các phần tử theo thứ tự từ bé đến lớn là:

    B=−118;1315;116

    Bài 2.5 trang 24 SBT Toán 7 Tập 1: Viết số thập phân 3,(5) dưới dạng phân số.

    Lời giải:

    3,(5)=3+0,(5)=3+5.0,(1)=3+5.19=3+59=329

    Xem thêm lời giải sách bài tập Toán lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

    Giải SBT Toán 7 trang 25 Tập 1

    Xem thêm lời giải sách bài tập Toán lớp 7 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

    Bài 6: Số vô tỉ. Căn bậc hai số học

    Bài 7: Tập hợp các số thực

    Ôn tập chương 2

    Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc

    Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết

    Xem thêm lời giải sách bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

    Bài 6: Số vô tỉ. Căn bậc hai số học

    Bài 7: Tập hợp các số thực

    Ôn tập chương 2

    Bài 8: Góc ở vị trí đặc biệt. Tia phân giác của một góc

    Bài 9: Hai đường thẳng song song và dấu hiệu nhận biết

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 582 30/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: