Nội dung bài viết

    Xem thêm

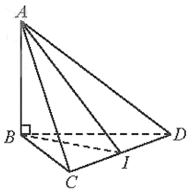
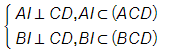    Cho tứ diện ABCD có tam giác BCD vuông cân tại B và AB vuông góc (BCD). Cho biết BC=a căn 2

    Lời giải Bài 1 trang 61 SBT Toán 11 Tập 2 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 358 15/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 11 Bài 3: Hai mặt phẳng vuông góc

    Bài 1 trang 61 SBT Toán 11 Tập 2: Cho tứ diện ABCD có tam giác BCD vuông cân tại B và AB ⊥ (BCD). Cho biết BC = a2 , AB = a3. Xác định và tính góc giữa hai mặt phẳng (ACD) và (BCD).

    Lời giải:

    Cho tứ diện ABCD có tam giác BCD vuông cân tại B và AB ⊥ (BCD)

    Gọi I là trung điểm của CD.

    Ta có: CD ⊥ BI và CD ⊥ AB suy ra CD ⊥ AI.

    Ta nhận thấy: CD là giao tuyến của 2 mặt phẳng (ACD) và (BCD);

    Mà Cho tứ diện ABCD có tam giác BCD vuông cân tại B và AB ⊥ (BCD)

    Suy ra ((ACD),  (BCD))=(AI,  BI)=AIB^.

    Tam giác BCD vuông cân tại B nên BI=12CD=12.BC.2=a.

    Xét tam giác ABI vuông tại B, ta có:

    tanAIB^=ABBI=13⇒AIB^=30°.

    Vậy góc giữa hai mặt phẳng (ACD) và (BCD) là AIB^=30° .

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1 trang 61 SBT Toán 11 Tập 2: Cho tứ diện ABCD có tam giác BCD vuông cân tại B và AB ⊥ (BCD)....

    Bài 2 trang 61 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a...

    Bài 3 trang 61 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và SA ⊥ (ABC)....

    Bài 4 trang 61 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Hai mặt phẳng (SAB)...

    Bài 5 trang 62 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a...

    Bài 6 trang 62 SBT Toán 11 Tập 2: Người ta cần sơn tất cả các mặt của một khối bê tông hình chóp cụt tứ giác đều...

    Bài 7 trang 62 SBT Toán 11 Tập 2: Một hộp đèn treo trần có hình dạng lăng trụ đứng lục giác đều (Hình 15),...

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 4: Khoảng cách trong không gian

    Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

    Bài tập cuối chương 8

    Bài 1: Biến cố giao và quy tắc nhân xác suất

    Bài 2: Biến cố hợp và quy tắc cộng xác suất

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 358 15/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: