Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J, K, L lần lượt là trọng tâm

a) Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

Do MN là đường trung bình của tam giác ABC nên MN // AC và MN = $\frac{1}{2}$AC.

Tương tự ta có QP là đường trung bình của tam giác ACD nên QP // AC và QP = $\frac{1}{2}$AC.

Suy ra MN // QP và MN = QP. (1)

Lại có I, J lần lượt là trọng tâm của các tam giác SAB, SBC nên $\frac{SJ}{SN}=\frac{SL}{SQ}=\frac{2}{3}$.

Suy ra IJ // MN và $\frac{IJ}{MN}=\frac{2}{3}$. (2)

Tương tự, ta có LK // QP và $\frac{LK}{QP}=\frac{2}{3}$. (3)

Từ (1), (2) và (3) suy ra IJ // LK và IJ = LK.

Vậy bốn điểm I, J, K, L đồng phẳng và tứ giác IJKL là hình bình hành.

b) Vì J, L lần lượt là trọng tâm của các tam giác SBC, SAD nên $\frac{SI}{SM}=\frac{SJ}{SN}=\frac{2}{3}$.

Suy ra JL // NQ.

Trong hình bình hành ABCD ta có NQ // CD (do N và Q lần lượt là trung điểm của BC và AD).

Do đó, JL // CD.

c) Hai mặt phẳng (IJKL) và (SCD) có điểm chung là K và lần lượt chứa hai đường thẳng JL và CD song song với nhau nên giao tuyến của hai mặt phẳng (IJKL) và (SCD) là đường thẳng d đi qua K và song song với CD.

*Phương pháp giải:

Nắm vững lý thuyết về hai đường thẳng song song trong không gian

* Một số lý thuyết và dạng bài thêm về hai đường thẳng song song trong không gian:

1. Vị trí tương đối giữa hai đường thẳng trong không gian

- Hai đường thẳng gọi là đồng phẳng nếu chúng cùng nằm trong một mặt phẳng.

- Hai đường thẳng gọi là chéo nhau nếu chúng không đồng phẳng. Hai đường thẳng chéo nhau thì không có điểm chung.

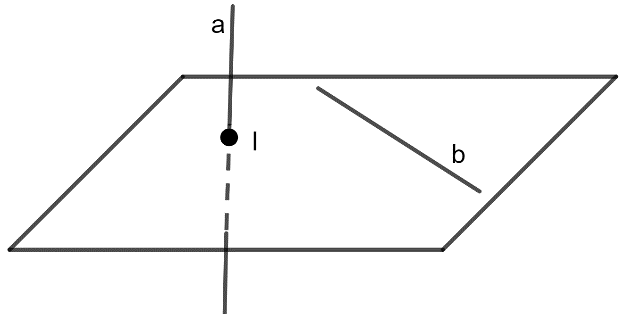
- Hai đường thẳng gọi là cắt nhau nếu chúng đồng phẳng và có một điểm chung.

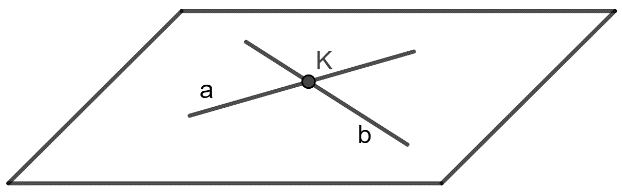
- Hai đường thẳng gọi là song song nếu chúng đồng phẳng và không có điểm chung.

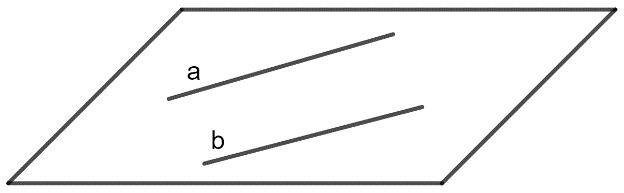
- Như vậy, trong không gian, có 4 vị trí tương đối của hai đường thẳng, đó là: song song, trùng nhau, cắt nhau và chéo nhau.

- Khi nhắc đến hai đường thẳng phân biệt, thì ta hiểu là có 3 vị trí tương đối của hai đường thẳng đó (bỏ đi trường hợp trùng nhau).

2. Hai đường thẳng song song

a. Tính chất của hai đường thẳng song song

Tính chất 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó.

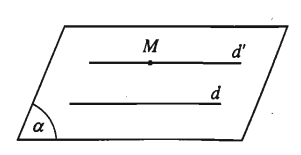
Tính chất 2: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.

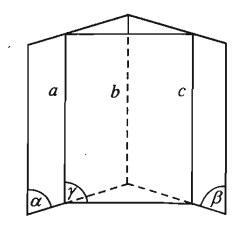
b. Định lý (về giao tuyến của ba mặt phẳng)

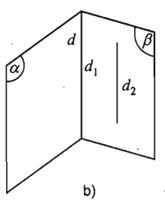
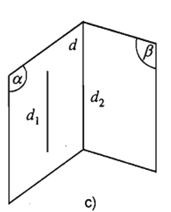
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song.

Giả sử (P), (Q), (R) là ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt a, b, c, trong đó: $a=\left(P\right)\cap \left(R\right),$ $b=\left(Q\right)\cap \left(R\right),$ $c=\left(P\right)\cap \left(Q\right)$. Khi đó:

TH1: a, b, c đồng quy

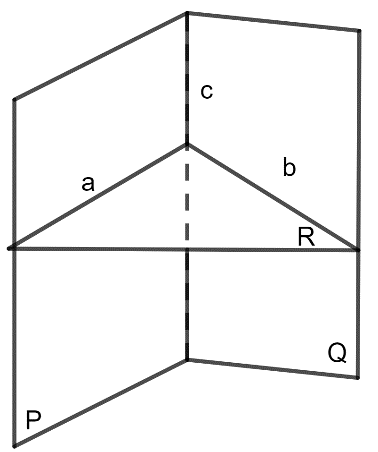
TH2: a // b // c

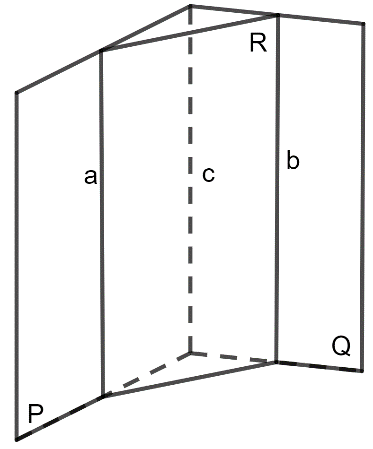
c. Hệ quả (Định lý về giao tuyến của ba mặt phẳng)

Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến (nếu có) của hai mặt phẳng nói trên sẽ song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

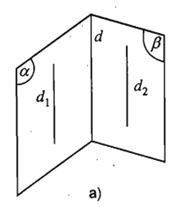
Các dạng bài tập về hai đường thẳng song song trong không gian

Dạng 1: Chứng minh hai đường thẳng song song

Phương pháp giải: Sử dụng một trong các cách sau

- Chứng minh hai đường thẳng đó đồng phẳng rồi áp dụng phương pháp chứng minh song song trong hình học phẳng.

- Chứng minh hai đường thẳng đó cùng song song với một đường thẳng thứ ba.

- Áp dụng định lí về giao tuyến song song.

- Áp dụng hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Dạng 2: Chứng minh bốn điểm đồng phẳng, ba đường thẳng đồng quy trong không gian

a. Chứng minh bốn điểm đồng phẳng

Phương pháp giải:

Chứng minh bốn điểm A, B, C, D đồng phẳng ta tìm hai đường thẳng a, b lần lượt đi qua hai trong bốn điểm trên và chứng minh a, b song song hoặc cắt nhau. Khi đó A, B, C, D thuộc mặt phẳng (a, b).

b. Chứng minh ba đường thẳng đồng quy

Phương pháp giải:

- Cách 1: Chứng minh đường thẳng thứ nhất đi qua giao điểm của hai đường thẳng còn lại.

- Cách 2: Chứng minh ba đường thẳng đôi một cắt nhau và chúng đôi một nằm trong ba mặt phẳng phân biệt

Bước 1: Xác định $\{\begin{array}{c}{d}_1,d_2\subset \left(P\right),d_1\cap d_2=I_1\\ d_2,d_3\subset \left(Q\right),d_2\cap d_3=I_2\\ d_3,d_1\subset \left(R\right),d_3\cap d_1=I_3\end{array}$ với (P), (Q), (R) phân biệt

Bước 2: Kết luận $d_1,d_2,d_3$ đồng quy tại $I\equiv I_1\equiv I_2\equiv I_3$

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

50 bài tập về Hai đường thẳng song song trong không gian (có đáp án 2024) và cách giải

Toán 11 Bài 2 giải vở bài tập (Cánh diều): Hai đường thẳng song song trong không gian