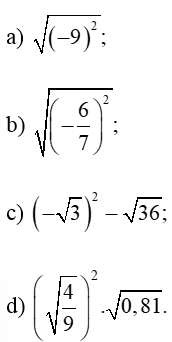Nội dung bài viết

    Xem thêm

    Lý thuyết Tính chất của phép khai phương - Toán 9 Chân trời sáng tạo

    Tóm tắt lý thuyết Toán lớp 9 Bài 3: Tính chất của phép khai phương hay, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 9.

    1 145 12/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 9 Bài 3: Tính chất của phép khai phương

    1. Căn thức bậc hai của một bình phương

    • Với mọi số thực a, ta có a2=a.

    • Với biểu thức A bất kì, ta có A2=A, nghĩa là

    + A2=A khi A ≥ 0 (tức là khi A nhận giá trị không âm)

    + A2=−A khi A < 0 (tức là khi A nhận giá trị âm)

    Ví dụ: Rút gọn các biểu thức sau:

    a) 2−32;

    b) 2n−72 với n > 5;

    c) a4 với a < 0.

    Hướng dẫn giải

    a) Ta có: 2−32=2−3=2−3 (vì 2−3>0).

    b) Ta có: 2n−72=2n−7

    Với n > 5, suy ra 2n−7>10−7>0.

    Do đó, 2n−72=2n−7.

    c) Ta có: a4=a22=a2=a2 (do a2 ≥ 0).

    2. Căn thức bậc hai của một tích

    • Với hai số thực a và b không âm, ta có:

    a.b=a.b.

    • Với hai biểu thức A và B nhận giá trị không âm, ta có:

    A.B=A.B.

    Ví dụ: Tính:

    a) 10.8;

    b) 1,6.3.5.

    Hướng dẫn giải

    a) Ta có: 10.8=10.8=180=62.5=65.

    b) Ta có: 1,6.3.5=1,6.3.5=24=22.6=26.

    • Với số thực a bất kì và b không âm, ta có

    a2b=ab.

    + Biến đổi này được gọi là đưa thừa số ra ngoài dấu căn.

    • Ngược lại, ta có biến đổi đưa thừa số vào trong dấu căn:

    + Nếu a ≥ 0 thì ab=a2b.

    + Nếu a < 0 thì ab=−a2b.

    Nhận xét: Tổng quát hơn, với hai biểu thức A, B mà B ≥ 0, ta có A2B=AB.

    Ví dụ: Đưa thừa số vào trong dấu căn bậc hai:

    a) 53

    b) −27;

    c) b3b với b > 0.

    Hướng dẫn giải

    a) Ta có: 53=52.3=75.

    b) Ta có: −27=−22.7=−28.

    c) Ta có: b3b=b2.3b=3b (vì b > 0).

    3. Căn thức bậc hai của một thương

    • Với số thực a không âm và số thực b dương, ta có

    ab=ab.

    • Với biểu thức A nhận giá trị không âm và biểu thức B nhận giá trị dương, ta có

    AB=AB.

    Ví dụ: Tính:

    a) 605;

    b) 16:8;

    c) 0,7:1,4.

    Hướng dẫn giải

    a) Ta có: 605=605=12=23.

    b) Ta có: 16:8=168=2.

    c) Ta có: 0,7:1,4=0,71,4=12=12=22.

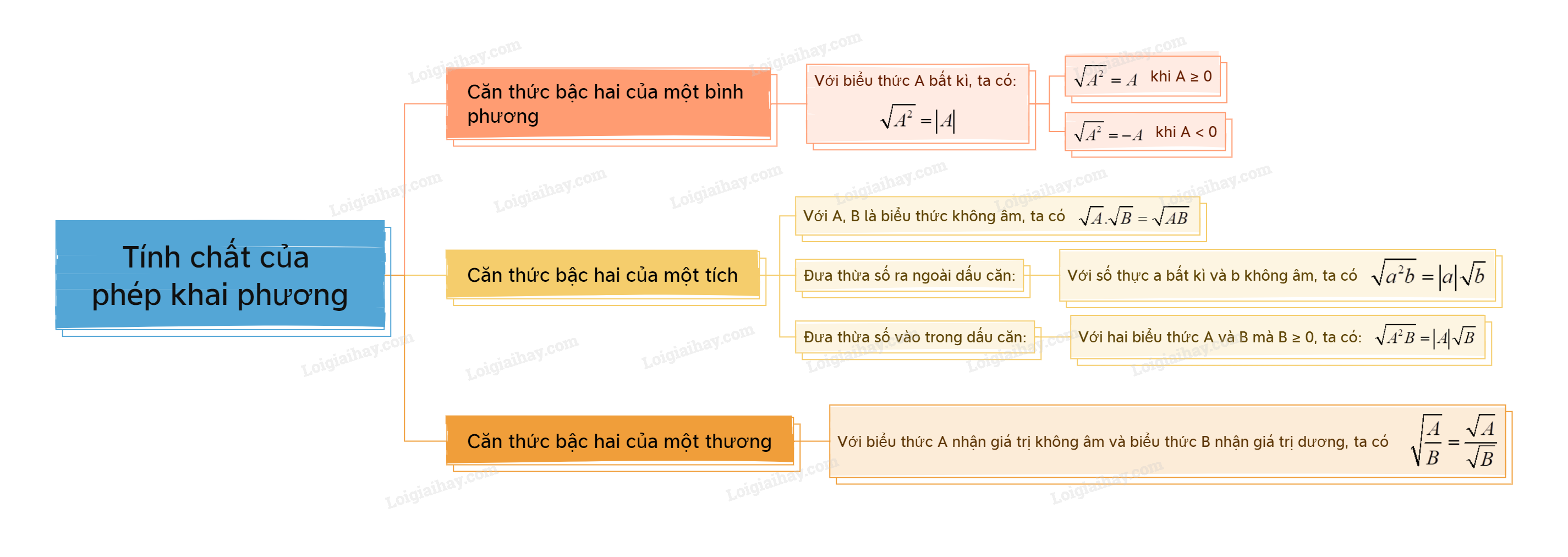
    Sơ đồ tư duy Tính chất của phép khai phương

    Lý thuyết Tính chất của phép khai phương - Toán 9 Chân trời sáng tạo (ảnh 1)

    Bài tập Tính chất của phép khai phương

    Bài 1. Rút gọn các biểu thức sau:

    a) 72.5;

    b) 100a2 với a < 0;

    c) 6b.24b−4b với b ≥ 0.

    Hướng dẫn giải

    a) Ta có: 72.5=75.

    b) Ta có: 100a2=10a2=10a=−10a với a < 0.

    c) Với b ≥ 0, ta có:

    6b.24b−4b=6b.24b−4b=144b2−4b

    =12b2−4b=12b−4b=12b−4b=8b

    Bài 2. Cho hình chữ nhật có chiều rộng a (cm), chiều dài b (cm) và diện tích S (cm2).

    a) Tìm S, biết a=6, b=48;

    b) Tìm a, biết S=56, b=3.

    Hướng dẫn giải

    a) Ta có: S = a.b

    =6.48=6.48

    =288=122

    Vậy S=122 cm2.

    b) Ta có: a = S : b

    =56:3

    =563=52

    Vậy a=52cm

    Bài 3. Tính:

    Tính chất của phép khai phương (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

    Hướng dẫn giải

    a) Ta có: −92=−9=9.

    b) Ta có: −672=−67=67.

    c) Ta có: −32−36=3−6=−3.

    d) 492.0,81=49.0,9=49.910=25.

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 145 12/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: