Lý thuyết Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Toán 9 Chân trời sáng tạo

Lý thuyết Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

1. Đường tròn ngoại tiếp tam giác

− Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác, khi đó tam giác được gọi là tam giác nội tiếp đường tròn.

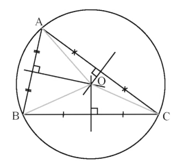
− Đường tròn ngoại tiếp tam giác có tâm là giao điểm của ba đường trung trực của tam giác và có bán kính bằng khoảng cách từ giao điểm đó đến một đỉnh bất kỳ của tam giác.

− Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác và bán kính bằng $\frac{a\sqrt{3}}{3}$.

− Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền và bán kính bằng nửa cạnh huyền.

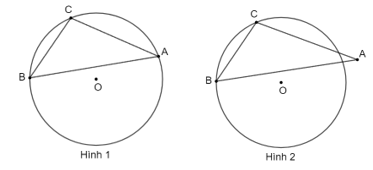
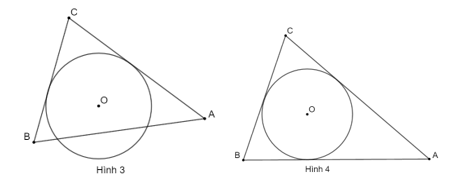
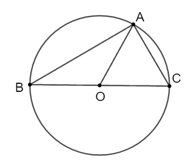
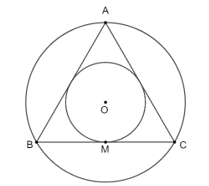
Ví dụ: Cho hình vẽ sau:

Hình nào có đường tròn (O) ngoại tiếp tam giác ABC? Giải thích?

Hướng dẫn giải:

Hình 1, đường tròn (O) là đường tròn ngoại tiếp tam giác ABC vì nó đi qua ba đỉnh A, B, C của tam giác ABC.

2. Đường tròn nội tiếp tam giác

− Đường tròn tiếp xúc với ba cạnh của tam giác gọi là đường tròn nội tiếp tam giác, khi đó tam giác được gọi là tam giác ngoại tiếp đường tròn.

− Đường tròn nội tiếp tam giác có tâm là giao điểm của ba đường phân giác trong và bán kính bằng khoảng cách từ giao điểm đó đến một cạnh bất kì của tam giác.

− Đường tròn nội tiếp tam giác đều có cạnh a có tâm là trọng tâm của tam giác và bán kính bằng $\frac{a\sqrt{3}}{6}$.

− Tam giác đều có tâm đường tròn nội tiếp và tâm đường tròn ngoại tiếp trùng nhau.

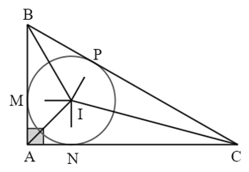
Ví dụ: Cho ∆ABC vuông tại A, có AB = 6 cm và AC = 8 cm ngoại tiếp đường tròn (I; r). Tính r.

Hướng dẫn giải:

Đường tròn (I; r) tiếp xúc với các cạnh AB, AC, BC theo thứ tự M, N, P.

Ta có:

⦁ $S_{AIB}=\frac{1}{2}IM.AB=\frac{1}{2}.r.AB$ (1)

⦁ $S_{AIC}=\frac{1}{2}IN.AC=\frac{1}{2}r.AC$ (2)

⦁ $S_{BIC}=\frac{1}{2}r.BC$ (3)

Cộng (1), (2), (3) vế theo vế, ta được:

$\frac{S_{AIB}+S_{AIC}+S_{BIC}}{S_{ABC}}=\frac{1}{2}r.\left(AB+AC+BC\right)$

Mà $S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}\mathrm{.6.8}=24$ (cm²), $BC=\sqrt{6^2+8^2}=10$ (cm)

Nên ta có: $24=\frac{1}{2}r.\left(6+8+10\right)$ nên $r=2$ (cm).

Vậy r = 2 cm.

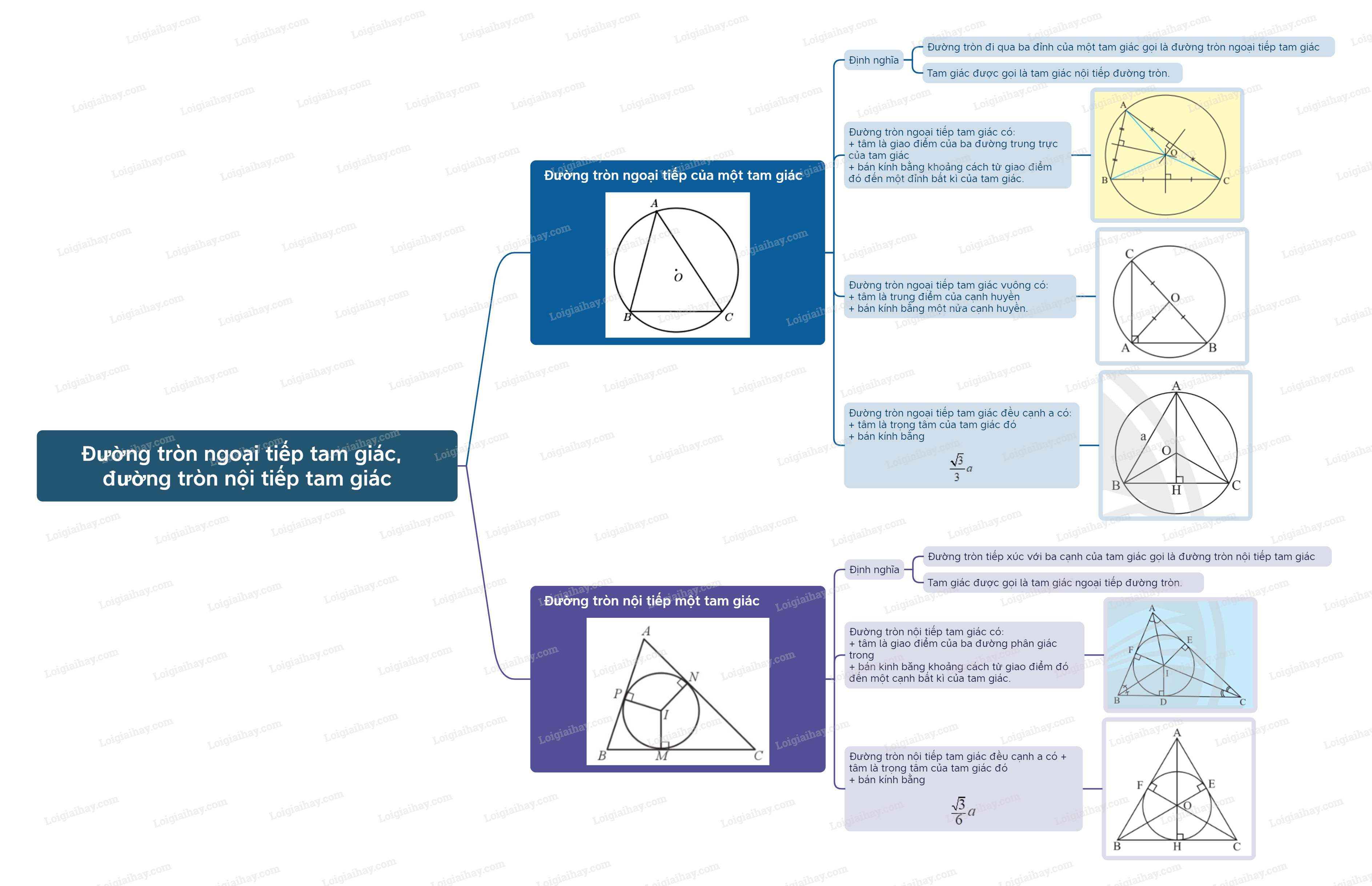
Sơ đồ tư duy Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

Bài tập Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

Bài 1. Cho tam giác ∆ABC vuông tại A, có AB = 10 cm và AC = $\sqrt{21}$ cm. Bán kính đường tròn ngoại tiếp tam giác ABC là

A. 5 cm.

B. 5,5 cm.

C. 6 cm.

D. 6,5 cm.

Hướng dẫn giải

Đáp án đúng là: B

Xét ∆ABC vuông tại A, theo định lý Pythagore ta có:

$B{C}^2=A{B}^2+A{C}^2={10}^2+{\left(\sqrt{21}\right)}^2=121$.

Suy ra BC = 11 (cm).

Tam giác ABC vuông tại A nên bán kính R đường tròn ngoại tiếp tam giác ABC bằng nửa cạnh huyền BC hay $R=\frac{BC}{2}=\frac{11}{2}=5,5$ (cm).

Bài 2. Cho tam giác ABC đều cạnh a ngoại tiếp đường tròn tâm O. Tính bán kính đường tròn nội tiếp tam giác ABC?

A. $\frac{a\sqrt{3}}{3}$.

B. $\frac{a\sqrt{3}}{2}$.

C. $\frac{a\sqrt{3}}{6}$.

D. $\frac{a\sqrt{2}}{3}$.

Hướng dẫn giải

Đáp án đúng là: C

Gọi M là trung điểm của BC. Ta có $BM=MC=\frac{BC}{2}=\frac{a}{2}$.

Do tam giác ABC đều nên tâm đường tròn nội tiếp tam giác ABC là trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC.

Áp dụng định lí Pythagore vào tam giác ABM ta có:

$A{M}^2=A{B}^2-B{M}^2=a^2-\frac{a^2}{4}=\frac{3a^2}{4}$, suy ra $AM=\frac{a\sqrt{3}}{2}.$

Bán kính đường tròn nội tiếp tam giác ABC là:

$r=OM=\frac{AM}{3}=\frac{a\sqrt{3}}{6}$.

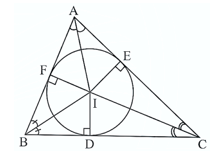
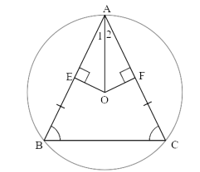
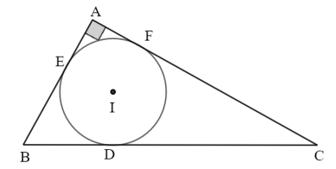
Bài 3. Cho ∆ABC cân tại A nội tiếp đường tròn (O). Gọi E, F theo thứ tự là hình chiếu của (O) lên AB và AC. Chứng minh rằng AO là tia phân giác của $\widehat{BAC}$.

Hướng dẫn giải

Ta có: ∆ABC cân tại A ⇒ AB = AC ⇒ OE = OF

Xét hai tam giác vuông AOE và AOF, có:

Cạnh OA chung

OE = OF (cmt)

Do đó ∆AOE = ∆AOF

Suy ra $\widehat{A_1}=\widehat{A_2}$ (hai góc tương ứng).

Do đó AO là phân giác của $\widehat{BAC}$.

Bài 4. Cho ∆ABC vuông tại A, $\widehat{BAC}=90°$ (AB ≤ AC) . Đường tròn (I) nội tiếp tam giác ABC tiếp xúc với BC tại D. Chứng minh $BD=\frac{BC+AB-AC}{2}$.

Hướng dẫn giải

Gọi E, F là tiếp điểm của đường tròn (I) với các cạnh AB, AC.

Theo tính chất của hai tiếp tuyến cắt nhau, ta có: AE = AF; BE = BD; CD = CF.

Do đó: 2BD = BD + BE

= BC – CD + AB – AE = BC + AB – (CD + AE)

= BC + AB – (CF + AF) = BC + AB – AC

Do đó $BD=\frac{BC+AB-AC}{2}$.

Bài 5. Cho tam giác ABC có AB = 6cm; BC= 10 cm và AC = 8cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC?

Hướng dẫn giải

Ta có: AB² + AC² = BC² ( = 100)

Suy ra tam giác ABC vuông tại A.

Do đó, tâm đường tròn ngoại tiếp tam giác ABC là trung điểm cạnh huyền BC.

Đường kính đường tròn là :

d = BC = 10 cm

Suy ra, bán kính đường tròn ngoại tiếp tam giác ABC là R = $\frac{d}{2}$ = 5 (cm).

Vậy R = 5 cm.