Nội dung bài viết

    Xem thêm

    Lý thuyết Hình cầu - Toán 9 Chân trời sáng tạo

    Tóm tắt lý thuyết Toán lớp 9 Bài 3: Hình cầu hay, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 9.

    1 108 14/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 9 Bài 3: Hình cầu

    1. Hình cầu

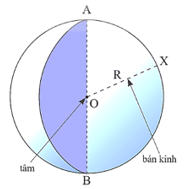
    Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định ta được một hình cầu tâm O, bán kính R.

    Khi đó, nửa đường tròn quét thành mặt cầu. Ta cũng gọi O và R lần lượt là tâm và bán kính của mặt cầu đó.

    Đoạn thẳng đi qua tâm của hình cầu với hai đầu mút nằm trên mặt cầu gọi là đường kính của hình cầu (hay mặt cầu).

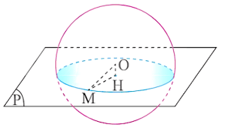
    Hình cầu (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

    Khi cắt hình cầu bởi một mặt phẳng thì phần chung của mặt cầu và mặt phẳng (còn gọi là mặt cắt) là một hình tròn.

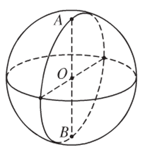
    Hình cầu (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

    Ví dụ: Hình cầu dưới đây có tâm O, đường kính AB, bán kính OA = OB.

    Khi cắt hình cầu bởi mặt phẳng đi qua AB (như hình vẽ) ta được một hình tròn.

    Hình cầu (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

    2. Diện tích của mặt cầu

    Diện tích của mặt cầu được tính bằng công thức:

    S = 4πR2.

    Trong đó: S là diện tích mặt cầu;

    R là bán kính.

    Ví dụ: Tính diện tích mặt cầu có bán kính 3 cm.

    Hướng dẫn giải:

    Diện tích của mặt cầu có bán kính 3 cm là:

    S = 4πR2 = 4π . 32 = 36π (cm2)

    3. Thể tích của hình cầu

    Thể tích của hình cầu được tính bằng công thức:

    V=43πR3.

    Trong đó: V là thể tích của hình cầu;

    R là bán kính.

    Ví dụ: Tính thể tích mặt cầu có bán kính 6 cm.

    Hướng dẫn giải:

    Thể tích tích của mặt cầu có bán kính 6 cm là:

    V=43πR3=43π.63=432π (cm3).

    Sơ đồ tư duy Hình cầu

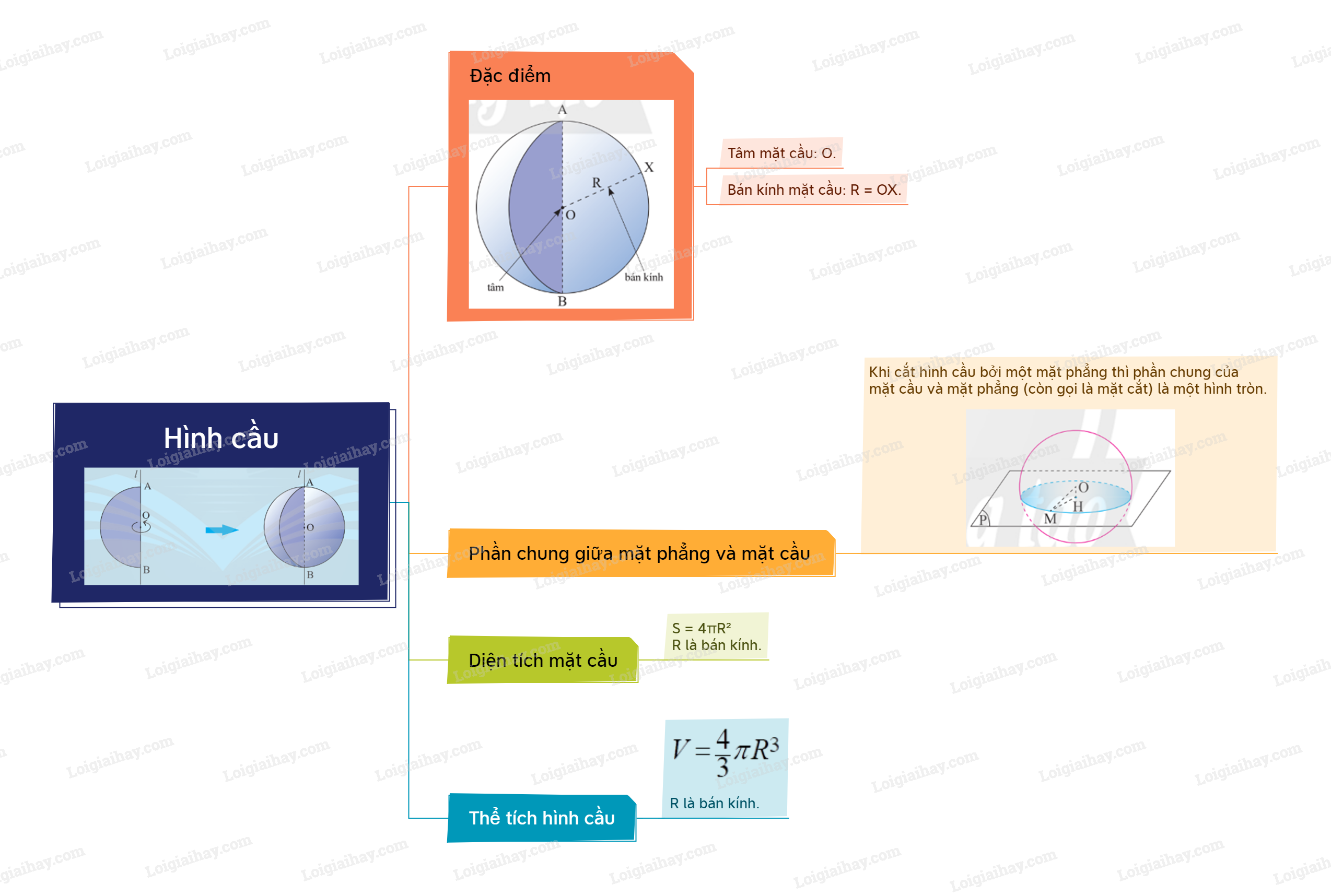
    Lý thuyết Hình cầu - Toán 9 Chân trời sáng tạo (ảnh 1)

    Bài tập Hình cầu

    Bài 1. Một hình cầu có số đo thể tích (tính bằng m3) bằng số đo diện tích mặt cầu (tính bằng m2). Bán kính hình cầu đó là

    A. 2 m.

    B. 3 m.

    C. 4 m.

    D. 5 m.

    Hướng dẫn giải

    Đáp án đúng là: B

    Gọi bán kính hình cầu là R (m).

    Vì số đo thể tích bằng số đo diện tích mặt cầu nên ta có:

    43πR3=4πR2 nên R = 3 (m).

    Vậy bán kính hình cầu đó là 3 m.

    Bài 2. Một hình cầu có thể tích bằng 972π cm3. Diện tích của mặt cầu đó là

    A. 234π cm2.

    B. 432π cm2.

    C. 324π cm2.

    D. 243π cm2.

    Hướng dẫn giải

    Đáp án đúng là: C

    Thể tích của hình cầu đó là:

    43πR3=972π hay nên R = 9 (cm)

    Diện tích của mặt cầu đó là:

    S = 4πR2 = 4π . 92 = 324π (cm2)

    Bài 3. Một hình cầu có bán kính bằng bán kính đáy của một hình nón. Biết đường sinh của hình nón bằng 12 cm và diện tích xung quanh của hình nón bằng diện tích mặt cầu. Tính thể tích hình cầu.

    Hướng dẫn giải

    Gọi bán kính hình cầu cũng như bán kính đáy hình nón là R.

    Diện tích xung quanh hình nón là: πRl = 12πR

    Diện tích mặt cầu là: 4πR2

    Vì diện tích xung quanh hình nón bằng diện tích mặt cầu nên:

    12πR = 4πR2 nên R = 3 (cm).

    Thể tích hình cầu là:

    V=43πR3=43π.33=36π (cm3)

    Vậy thể tích hình cầu đó là 36π cm3.

    Bài 4. Một hình cầu nội tiếp một hình trụ. Biết diện tích toàn phần hình trụ là 384π cm2. Tính thể tích hình cầu.

    Hướng dẫn giải

    Gọi bán kính hình cầu là R thì bán kính đáy hình trụ là R và chiều cao hình trụ là 2R.

    Vì diện tích toàn phần hình trụ là 384π cm2 nên ta có:

    2πR(2R + R) = 384π hay 6πR2 = 384π nên R = 8 (cm).

    Thể tích hình cầu là:

    V=43πR3=43π.83=20483π (cm3)

    Vậy thể tích hình cầu đó là 20483π cm3.

    Bài 5. Một chiếc thuyền thúng có dạng nửa hình cầu, có khối lượng 45kg, người chèo thuyền khối lượng 65kg. Biết đường kính của thuyền là 1,2m và trên thuyền có thêm 2,4 tạ cá, hỏi nước có ngập đến mép thuyền không? Biết khối lượng riêng của nước là

    1 kg/dm3 và nếu khối lượng riêng của thuyền nhỏ hơn khối lượng riêng của nước thì nước không ngập đến mép thuyền và ngược lại.

    Hướng dẫn giải

    Bán kính của thuyền thúng là:

    1,2 : 2 = 0,6 (m) = 6 (dm).

    Thể tích của thuyền là:

    V=12.43πR3=12.43π.63=144π (dm3) ≈ 425 (dm3)

    Tổng khối lượng của thuyền, người và cá là:

    45 + 65 + 240 = 350 (kg)

    Khối lượng riêng của thuyền là:

    350 : 452 = 0,8 (kg/dm3)

    Khối lượng riêng của nước là 1 kg/dm3.

    Vậy khối lượng riêng của thuyền nhỏ hơn khối lượng riêng của nước nên nước không ngập đến mép thuyền.

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 108 14/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: