Tổng hợp lý thuyết Chương 1– Toán lớp 9 Chân trời sáng tạo

Lý thuyết Toán 9: Bài tập cuối Chương 1 - Chân trời sáng tạo

A. Tổng hợp lý thuyết Toán 9 Chương 1

1. Phương trình tích

Muốn giải phương trình (a₁x + b₁)(a₂x + b₂) = 0, ta giải hai phương trình a₁x + b₁ = 0 và a₂x + b₂ = 0, rồi lấy tất cả các nghiệm của chúng.

Chú ý: Trong nhiều trường hợp, để giải một phương trình, ta biến đổi để đưa phương trình đó về phương trình tích.

2. Phương trình chứa ẩn ở mẫu quy về phương trình bậc nhất

2.1. Điều kiện xác định của phương trình

Đối với phương trình chứa ẩn ở mẫu, điều kiện của ẩn để tất cả các mẫu thức trong phương trình đều khác 0 gọi là điều kiện xác định của phương trình.

Nhận xét:Những giá trị của ẩn không thỏa mãn điều kiện xác định không thể là nghiệm của phương trình.

2.2. Giải phương trình chứa ẩn ở mẫu

Các bước giải phương trình chứa ẩn ở mẫu

Bước 1. Tìm điều kiện xác định của phương trình.

Bước 2. Quy đồng mẫu thức hai vế của phương trình, rồi khử mẫu.

Bước 3. Giải phương trình vừa nhận được.

Bước 4. Xét mỗi giá trị tìm được ở Bước 3, giá trị nào thỏa mãn điều kiện xác định thì đó là nghiệm của phương trình đã cho.

3. Phương trình bậc nhất hai ẩn

Phương trình bậc nhất hai ẩn x và y là hệ thức có dạng

ax + b = c,

trong đó a, b, c là các số đã biết (gọi là hệ số), a và b không đồng thời bằng 0.

Nếu giá trị của vế trái tại x = x₀ và y = y₀ bằng vế phải thì cặp số (x₀; y₀) được gọi là một nghiệm của phương trình.

Giải phương trình là tìm tất cả các nghiệm của phương trình đó.

4. Hệ hai phương trình bậc nhất hai ẩn

Hệ hai phương trình bậc nhất hai ẩn x, y có dạng:

$\left(\mathrm{I}\right)\left\{\begin{array}{l}\text{ax}+\mathrm{by}=\mathrm{c}\left(1\right)\\ ax+{\mathrm{b}}^{\text{'}}\mathrm{y}={\mathrm{c}}^{\text{'}}.\left(2\right)\end{array}\right.$

Giải hệ phương trình là tìm tất cả các nghiệm của hệ phương trình đó.

5. Giải hệ phương trình bằng phương pháp thế

Các bước giải hệ phương trình bằng phương pháp thế

Bước 1. Từ một phương trình của hệ, ta biểu diễn ẩn này theo ẩn kia, rồi thế vào phương trình còn lại của hệ để nhận được một phương trình một ẩn.

Bước 2. Giải phương trình một ẩn đó rồi suy ra nghiệm của hệ.

6. Giải hệ phương trình bằng phương pháp cộng đại số

Các bước giải hệ phương trình bằng phương pháp cộng đại số

Bước 1. Nhân hai vế của mỗi phương trình với mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.

Bước 2. Cộng hay trừ từng vế hai phương trình của hệ để được một phương trình một ẩn và giải phương trình đó.

Bước 3. Thế giá trị của ẩn tìm được ở Bước 2 vào một trong hai phương trình của hệ đã cho để tìm giá trị của ẩn còn lại. Kết luận hệ của nghiệm.

7. Giải bài toán bằng cách lập hệ phương trình

Các bước giải bài toán bằng cách lập hệ phương trình

Bước 1. Lập hệ phương trình

− Chọn hai ẩn biểu thị hai đại lượng chưa biết và đặt điều kiện thích hợp cho các ẩn.

− Biểu diễn các đại lượng liên quan theo các ẩn và các đại lượng đã biết.

− Lập hệ hai phương trình bậc nhất hai ẩn biểu thị mối quan hệ giữa các đại lượng.

Bước 2. Giải hệ phương trình nhận được.

Bước 3. Kiểm tra nghiệm tìm được ở Bước 2 có thỏa mãn điều kiện của ẩn hay không, rồi trả lời bài toán.

B. Bài tập Bài tập cuối chương 1

Bài 1. Tìm điều kiện xác định của mỗi phương trình sau:

a) $\frac{x+2}{4x-1}=1;$

b) $1-\frac{2}{x-3}=\frac{x+1}{2x-1}.$

Hướng dẫn giải

a) Điều kiện xác định của phương trình là 4x – 1 ≠ 0 hay $x\ne \frac{1}{4}$

b) Ta có x – 3 ≠ 0 khi x ≠ 3 và 2x – 1 ≠ 0 khi $x\ne \frac{1}{2}$

Vậy điều kiện xác định của phương trình là x ≠ 3 và $x\ne \frac{1}{2}$

Bài 2. Giải các phương trình:

a) 4x(x + 2) = 0;

b) (2x – 8)(x – 7) = 0;

c) 3x – x² = 0;

d) (x – 4)² – 25x² = 0.

Hướng dẫn giải

a) Ta có 4x(x + 2) = 0

4x = 0 hoặc x + 2 = 0

x = 0 hoặc x = –2.

Vậy phương trình đã cho có hai nghiệm là x = 0 và x = –2.

b) Ta có (2x – 8)(x – 7) = 0

2x – 8 = 0 hoặc x – 7 = 0

2x = 8 hoặc x = 7

x = 4 hoặc x = 7.

Vậy phương trình đã cho có hai nghiệm là x = 4 và x = 7.

c) Ta có 3x – x² = 0

x(3 – x) = 0

x = 0 hoặc 3 – x = 0

x = 0 hoặc x = 3.

Vậy phương trình đã cho có hai nghiệm là x = 0 và x = 3.

d) Ta có (x – 3)² – 16x² = 0

(x – 3)² – (4x)² = 0

(x – 3 + 4x)(x – 3 – 4x) = 0

(5x – 3)(–3x – 3) = 0

5x – 3 = 0 hoặc –3x – 3 = 0

5x = 3 hoặc 3x = –3

$x=\frac{3}{5}$hoặc x = –1.

Vậy phương trình đã cho có hai nghiệm là $x=\frac{3}{5}$và x = –1.

Bài 3. Giải các phương trình:

a) $\frac{2x}{x+2}-2=\frac{x}{x+2}$

b) $\frac{x-1}{x-3}-\frac{1}{x+3}=\frac{3x+3}{\left(x-3\right)\left(x+3\right)}$

c) $\frac{x-1}{x+2}-\frac{x}{x-2}=\frac{4-6x}{x^2-4}.$

Hướng dẫn giải

a) Điều kiện xác định: x + 2 ≠ 0 hay x ≠-2.

Ta có $\frac{2x}{x+2}-2=\frac{x}{x+2}$

$\frac{2x-2\left(x+2\right)}{x+2}=\frac{x}{x+2}$

2x – 2(x + 2) = x

2x – 2x – 4 = x

x = -4 (thỏa mãn điều kiện)

Vậy phương trình đã cho có hai nghiệm là x = –4.

b) Điều kiện xác định: x ≠ 3 và x ≠ –3.

Ta có $\frac{x-1}{x-3}-\frac{1}{x+3}=\frac{3x+3}{\left(x-3\right)\left(x+3\right)}$

$\frac{\left(x-1\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}-\frac{x-3}{\left(x-3\right)\left(x+3\right)}=\frac{3x+3}{\left(x-3\right)\left(x+3\right)}$

(x – 1)(x + 3) – (x – 3) = 3x + 3

x² + 2x – 3 – x + 3 = 3x + 3

x² + x = 3x + 3

x(x + 1) = 3(x + 1)

x(x + 1) -3(x + 1) = 0

(x + 1)(x -3) = 0

x + 1 = 0 hoặc x -3 = 0

x =-1 (thỏa mãn điều kiện) hoặc x = 3 (không thỏa mãn điều kiện).

Vậy phương trình đã cho có hai nghiệm là x = -1.

c) Điều kiện xác định: x ≠ 2 và x ≠ –2.

Ta có $\frac{x-1}{x+2}-\frac{x}{x-2}=\frac{4-6x}{x^2-4}$

$\frac{x-1}{x+2}-\frac{x}{x-2}=\frac{4-6x}{\left(x-2\right)\left(x+2\right)}$

$\frac{\left(x-1\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\frac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{4-6x}{\left(x-2\right)\left(x+2\right)}$

$\frac{x^2-x-2x+2}{\left(x-2\right)\left(x+2\right)}-\frac{x^2+2x}{\left(x-2\right)\left(x+2\right)}=\frac{4-6x}{\left(x-2\right)\left(x+2\right)}$

$\frac{-5x+2}{\left(x-2\right)\left(x+2\right)}=\frac{4-6x}{\left(x-2\right)\left(x+2\right)}$

-5x + 2 = 4 - 6x

6x - 5x = 4 - 2

x = 2 (không thỏa mãn điều kiện xác định).

Vậy phương trình đã cho vô nghiệm.

Bài 4. Trong các hệ phương trình sau, hệ phương trình nào là hệ phương trình bậc nhất hai ẩn?

a) $\left\{\begin{array}{l}x-\frac{1}{2}y=1\\ 4x+y=2;\end{array}\right.$

b) $\left\{\begin{array}{l}2x+3y=-1\\ 0x+0y=7;\end{array}\right.$

c) $\left\{\begin{array}{l}\frac{1}{3}x-y=2\\ 0x+\sqrt{3}y=-1.\end{array}\right.$

Hướng dẫn giải

a) Hệ phương trình $\left\{\begin{array}{l}x-\frac{1}{2}y=1\\ 4x+y=2\end{array}\right.$là hệ phương trình bậc nhất hai ẩn với a = 1, $b=-\frac{1}{2},$c = 1, a' = 4, b' = 1, c' = 2.

b) Hệ phương trình $\left\{\begin{array}{l}2x+3y=-1\\ 0x+0y=7\end{array}\right.$>không phải là hệ phương trình bậc nhất hai ẩn vì a' = b' = 0.

c) Hệ phương trình $\left\{\begin{array}{l}\frac{1}{3}x-y=2\\ 0x+\sqrt{3}y=-1\end{array}\right.$là hệ phương trình bậc nhất hai ẩn với $a=\frac{1}{3},$b = –1, c = 2, a' = 0, $b\text{'}=\sqrt{3},$c' = –1.

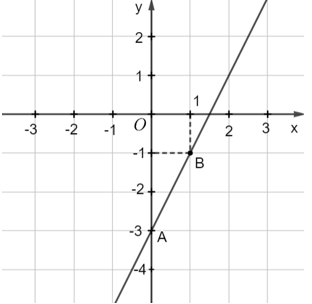
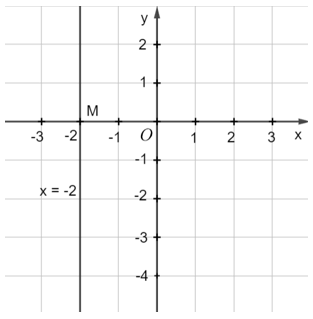
Bài 5. Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) 2x – y = 3;

b) x + 0y = −2.

Hướng dẫn giải

a) Viết lại phương trình thành y = 2x – 3.

Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d: y = 2x – 3 (như hình vẽ).

b) Viết lại phương trình thành x = −2.

Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d vuông góc với Ox tại điểm M(−2; 0).

Bài 6. Giải các hệ phương trình:

a) $\left\{\begin{array}{l}x+2y=5\\ 2x-5y=1;\end{array}\right.$

b) $\left\{\begin{array}{l}5x+6y=6\\ 5x+2y=2;\end{array}\right.$

c) $\left\{\begin{array}{l}5x-4y=3\\ 2x+y=4.\end{array}\right.$

Hướng dẫn giải

a) $\left\{\begin{array}{l}x+2y=5\\ 2x-5y=1\end{array}\right.$

$\left\{\begin{array}{l}x=5-2y\\ 2(5-2y)-5y=1\end{array}\right.$

$\left\{\begin{array}{l}x=5-2y\\ -9y=-9\end{array}\right.$

$\left\{\begin{array}{l}x=3\\ y=1\end{array}\right.$

Vậy hệ phương trình có nghiệm duy nhất là (3; 1).

b) $\left\{\begin{array}{l}5x+6y=6\\ 5x+2y=2\end{array}\right.$

$\left\{\begin{array}{l}5x+6y-(5x+2y)=6-2\\ x=\frac{2-2y}{5}\end{array}\right.$

$\left\{\begin{array}{l}4y=4\\ x=\frac{2-2y}{5}\end{array}\right.$

$\left\{\begin{array}{l}y=1\\ x=0\end{array}\right.$

Vậy hệ phương trình có nghiệm duy nhất là (0; 1).

c) $\left\{\begin{array}{l}5x-4y=3\\ 2x+y=4\end{array}\right.$

$\left\{\begin{array}{l}5x-4\left(4-2x\right)=3\\ y=4-2x\end{array}\right.$

$\left\{\begin{array}{l}5x-16+8x=3\\ y=4-2x\end{array}\right.$

$\left\{\begin{array}{l}13x=19\\ y=4-2x\end{array}\right.$

$\left\{\begin{array}{l}x=\frac{19}{13}\\ y=\frac{14}{13}\end{array}\right.$

Vậy hệ phương trình có nghiệm duy nhất là $\left(\frac{19}{13};\frac{14}{13}\right)$

Bài 7. Giải các hệ phương trình:

a) $\left\{\begin{array}{l}8x-4y=-12\\ -8x+9y=3;\end{array}\right.$

b) $\left\{\begin{array}{l}12x+18y=-24\\ -2x-3y=4;\end{array}\right.$

c) $\left\{\begin{array}{l}\left(x+1\right)\left(y-1\right)=xy-1\\ \left(x-3\right)(y-3)=xy-3.\end{array}\right.$

Hướng dẫn giải

a) Cộng từng vế hai phương trình của hệ mới, ta được 5y = –9 hay $y=-\frac{9}{5}.$

Thế $y=-\frac{9}{5}$vào phương trình thứ nhất của hệ đã cho, ta có $2x+\frac{9}{5}=–3$hay $2x=-\frac{24}{5},$ suy ra $x=-\frac{12}{5}.$

Vậy hệ phương trình đã cho có nghiệm là $\left(-\frac{12}{5};-\frac{9}{5}\right).$

b) Nhân hai vế của phương trình thứ hai với 6, ta được hệ phương trình sau:

$\left\{\begin{array}{l}12x+18y=-24\\ -12x-18y=24.\end{array}\right.$

Cộng từng vế hai phương trình của hệ trên, ta được phương trình:

0x + 0y = 0, hay 0x = 0. Phương trình này có vô số nghiệm x ∈ ℝ.

Từ phương trình thứ hai ta có 3y = –2x – 4, suy ra $y=-\frac{2}{3}x-\frac{4}{3}.$

Vậy hệ phương trình đã cho có vô số nghiệm $\left\{\begin{array}{l}x\in ℝ\\ y=-\frac{2}{3}x-\frac{4}{3}.\end{array}\right.$

c) $\left\{\begin{array}{l}\left(x+1\right)\left(y-1\right)=xy-1\\ \left(x-3\right)(y-3)=xy-3\end{array}\right.$

$\left\{\begin{array}{l}xy-x+y-1=xy-1\\ xy-3x-3y+9=xy-3\end{array}\right.$

$\left\{\begin{array}{l}-x+y=0\\ -3x-3y=-12\end{array}\right.$

$\left\{\begin{array}{l}x-y=0\\ x+y=4\end{array}\right.$

$\left\{\begin{array}{l}x=y\\ x+y=4\end{array}\right.$

$\left\{\begin{array}{l}x=y\\ 2x=4\end{array}\right.$

$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$

Vậy hệ phương trình có nghiệm duy nhất là (2; 2).

Bài 8. Xác định a, b để đồ thị hàm số y = ax + b đi qua hai điểm A(2; 1) và B(4; –2).

Hướng dẫn giải

• Đồ thị hàm số y = ax + b đi qua hai điểm A(2; 1) nên

1 = a . 2 + b hay 2a + b = 1.(1)

• Đồ thị hàm số y = ax + b đi qua hai điểm B(4; –2) nên

–2 = a . 4 + b hay 4a + b = –2.(2)

Từ (1) và (2) ta có hệ phương trình $\left\{\begin{array}{l}2a+b=1\\ 4a+b=-2\end{array}\right.$(I)

Trừ từng vế hai phương trình của hệ (I), ta được –2a = 3. Suy ra $a=-\frac{3}{2}$

Thay $a=-\frac{3}{2}$vào phương trình thứ nhất của hệ (I), ta được

$2\cdot \left(-\frac{3}{2}\right)+b=1$hay –3 + b = 1 nên b = 4.

Vậy $a=-\frac{3}{2}$; b = 4.

Bài 9. Một khách du lịch đi trên ôtô 4 giờ, sau đó đi tiếp bằng tàu hỏa trong 7 giờ được quãng đường dài 640km. Hỏi vận tốc của tàu hỏa và ôtô, biết rằng mỗi giờ tàu hỏa đi nhanh hơn ôtô 5km?

Hướng dẫn giải

Gọi x (km/h) là vận tốc của xe ôtô (x > 0);

y (km/h) là vận tốc của tàu hỏa (y > 0).

Quãng đường đi được bằng ôtô là: 4x (km).

Quãng đường đi được tàu hỏa là: 7y (km).

Tổng quãng đường đi được là 640km nên ta có: 4x + 7y = 640 (km) (1)

Mỗi giờ tàu hỏa đi nhanh hơn ôtô 5km nên ta có: y − x = 5 (km) (2)

Từ (1) và (2), ta có hệ phương trình:

$\left\{\begin{array}{l}4x+7y=640\\ y-x=5\end{array}\right.$

$\left\{\begin{array}{l}4x+7y=640\\ y=x+5\end{array}\right.$

$\left\{\begin{array}{l}4x+7(x+5)=640\\ y=x+5\end{array}\right.$

$\left\{\begin{array}{l}11x=605\\ y=x+5\end{array}\right.$

$\left\{\begin{array}{l}x=55\\ y=60\end{array}\right.$ (thỏa mãn điều kiện)

Vậy vận tốc của ôtô là 55 km/h và vận tốc của tàu hỏa là 60km/h.

Bài 10. Hai vòi nước cùng chảy vào một bể cạn trong 18 giờ thì đầy bể. Nếu vòi 1 chảy trong 4 giờ, vòi 2 chảy trong 7 giờ thì chỉ được $\frac{1}{3}$bể. Hỏi nếu mỗi vòi chảy một mình thì trong bao lâu sẽ đầy bể?

Hướng dẫn giải

Gọi x (bể) là phần nước của bể vòi một chảy được trong 1 giờ (x > 0)

y (bể) là phần nước của bể vòi hai chảy dược trong 1 giờ (y > 0)

Hai vòi nước cùng chảy vào một bể cạn trong 18 giờ thì đầy bể nên

18x + 18y = 1.(1)

Vòi 1 chảy trong 4 giờ, vòi 2 chảy trong 7 giờ thì chỉ được $\frac{1}{3}$ bể nên

4x + 7y = $\frac{1}{3}.$(2)

$\left\{\begin{array}{l}18x+18y=1\\ 4x+7y=\frac{1}{3}\end{array}\right.$

$\left\{\begin{array}{l}18x+18y=1\\ x=\frac{1}{4}\left(\frac{1}{3}-7y\right)\end{array}\right.$

$\left\{\begin{array}{l}\frac{18}{4}\left(\frac{1}{3}-7y\right)+18y=1\\ x=\frac{1}{4}\left(\frac{1}{3}-7y\right)\end{array}\right.$

$\left\{\begin{array}{l}\frac{-27}{2}y=-\frac{1}{2}\\ x=\frac{1}{4}\left(\frac{1}{3}-7y\right)\end{array}\right.$

$\left\{\begin{array}{l}y=\frac{1}{27}\\ x=\frac{1}{54}\end{array}\right.$(thỏa mãn điều kiện)

Ta có vòi 1 mỗi giờ chảy được $\frac{1}{54}$bể suy ra vòi 1 chảy một mình 54 giờ thì đầy bể,

vòi 2 mỗi giờ chảy được $\frac{1}{27}$bể suy ra vòi 2 chảy một mình 27 giờ thì đầy bể.

Vậy vòi 1 chảy một mình 54 giờ thì đầy bể, vòi 2 chảy một mình trong 27 giờ thì đầy bể.

Bài 11. Để chuẩn bị cho buổi liên hoan của gia đình, cô Lan mua hai loại thực phẩm là thịt lợn và cá chép. Giá tiền thịt lợn là 120 nghìn đồng/kg, giá tiền cá chép là 50 nghìn đồng/kg. Cô Lan đã chi 290 nghìn để mua 3 kg hai loại thực phẩm trên. Gọi x và y lần lượt là số kilôgam thịt lợn và cá chép mà cô Lan đã mua.

a) Viết hệ hai phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng.

b) Cặp số (2; 1) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Hướng dẫn giải

a) Cô Lan đã mua 3 kg hai loại thực phẩm (thịt lợn và cá chép) nên ta có phương trình:

x + y = 3. (1)

Số tiền cô Lan đã chi để mua x kilôgam thịt lợn là 120x (nghìn đồng).

Số tiền cô Lan đã chi để mua y kilôgam cá chép là 50y (nghìn đồng).

Theo bài, cô Lan đã chi 295 nghìn để mua hai loại thực phẩm trên nên ta có phương trình: 120x + 50y = 290. (2)

Từ (1) và (2) ta có hệ phương trình bậc nhất hai ẩn x, y biểu thị mối quan hệ giữa các đại lượng: $\left\{\begin{array}{l}x+y=3\\ 120x+50y=290.\end{array}\right.$

b) Thay x = 2 và y = 1 vào mỗi phương trình trong hệ $\left\{\begin{array}{l}x+y=3\\ 120x+50y=290,\end{array}\right.$ ta có:

2 + 1 = 3;

120. 2 + 50. 1 = 240 + 50 = 290.

Do đó, cặp số (2; 1) là nghiệm của từng phương trình trong hệ.

Vậy cặp số (2; 1) là nghiệm của hệ phương trình ở câu a.