Lý thuyết Hình quạt tròn và hình vành khuyên - Toán 9 Chân trời sáng tạo

Lý thuyết Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên

1. Độ dài cung tròn

• Người ta chứng minh được tỉ số giữa chu vi và đường kính của một đường tròn luôn bằng một số không đổi gọi là π (ta thường lấy π ≈ 3,14 hoặc lấy π theo máy tính).

• Độ dài của cung tỉ lệ thuận với số đo của chúng.

• Ta có công thức tính chu vi C của đường tròn là: C = πd = 2πR, trong đó d là đường kính và R là bán kính.

• Trên đường tròn bán kính R, độ dài ℓ của một cung có số đo n° được tính theo công thức: $\mathcal{l}=\frac{\pi Rn}{180}.$

Ví dụ: Tính độ dài cung 60° của một đường tròn có bán kính 15 cm. (Lấy π theo máy tính và làm tròn kết quả đến hàng phần mười).

Hướng dẫn giải

Cung 60°, bán kính R = 15 cm có độ dài là:

$\mathcal{l}=\frac{\pi Rn}{180}=\frac{\pi \mathrm{.15.60}}{180}=5\pi \approx 15,7$ (cm).

Vậy độ dài cung 60° của một đường tròn có bán kính 15 cm khoảng 15,7 cm.

2. Hình quạt tròn

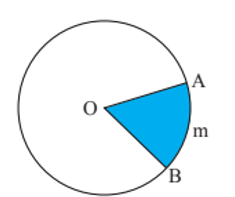
• Hình quạt tròn là một phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai mút của cung đó.

• Diện tích hình quạt tròn bán kính R, ứng với cung n° được tính theo công thức: $S=\frac{\pi R^{2}n}{360}.$

Ví dụ: Tính diện tích hình quạt tròn bán kính R = 5 cm, ứng với cung 30° (kết quả làm tròn đến hàng phần trăm của cm²).

Hướng dẫn giải

Hình quạt tròn bán kính R = 5 cm, ứng với cung 30° có diện tích là:

$S=\frac{\pi R^{2}n}{360}=\frac{\pi .5^2.30}{360}\approx 6,54$ (cm²).

Chú ý:

• Hình quạt tròn giới hạn bởi hai bán kính OA, OB và cung tròn AmB được gọi là hình quạt tròn OAmB hoặc hình quạt tròn OAB.

• Người ta chứng minh được diện tích hình quạt tròn tỉ lệ thuận với số đo của cung ứng với nó.

3. Hình vành khuyên

• Cho hai đường tròn đồng tâm (O; R) và (O; r) với R > r. Hình vành khuyên là phần mặt phẳng giới hạn bởi hai đường tròn (O; r) và (O; R).

• Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) được tính bởi công thức: $S=\pi \left(R^2-r^2\right).$

Ví dụ: Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 6 cm) và (O; 10 cm) (kết quả làm tròn đến hàng phần trăm).

Hướng dẫn giải

Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 6 cm) và (O; 10 cm) là:

$S=\pi \left(R^2-r^2\right)=\pi \left({10}^2-8^2\right)=36\pi \approx 113,09$ (cm²).

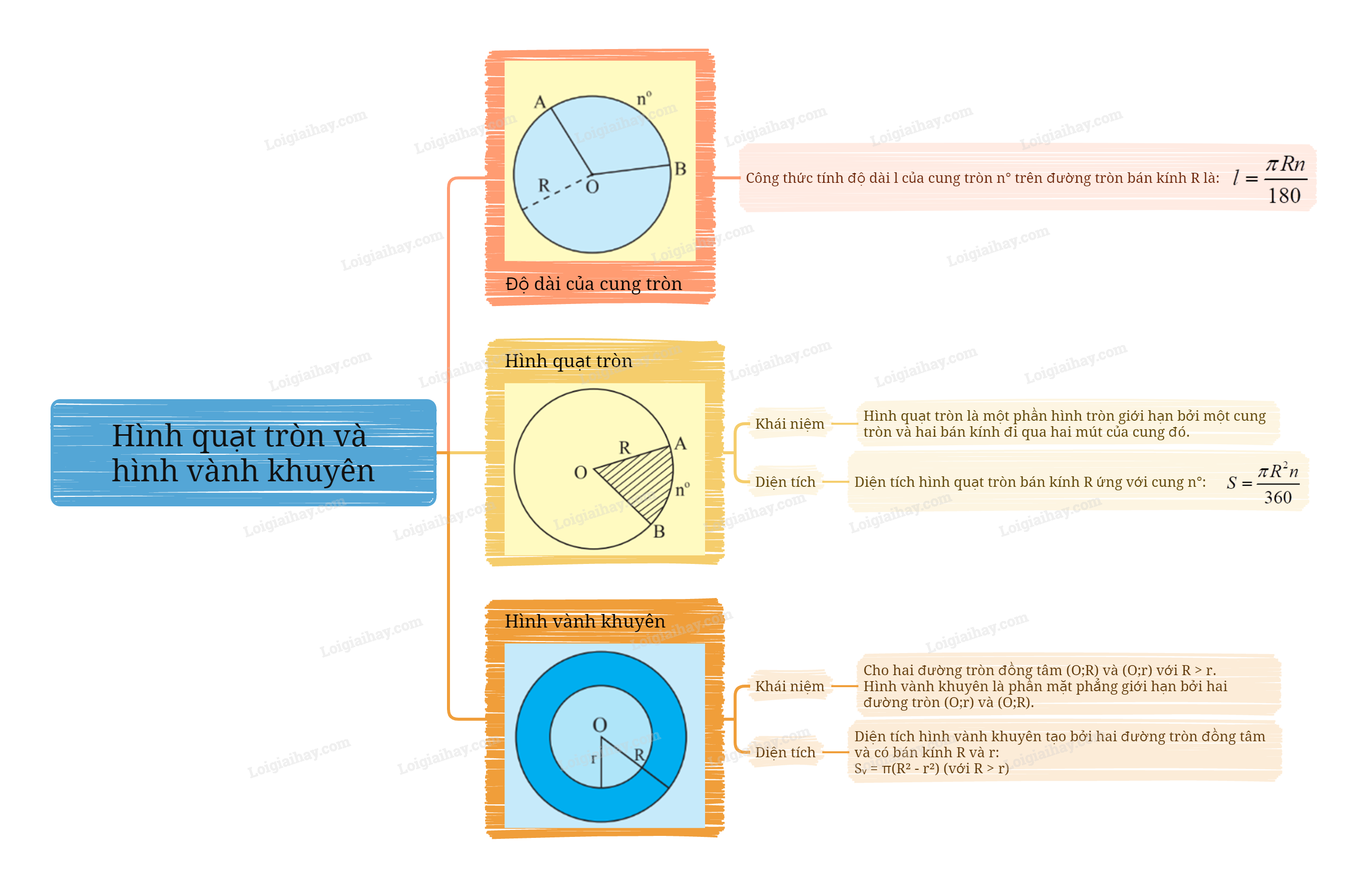
Sơ đồ tư duy Hình quạt tròn và hình vành khuyên

Bài tập Hình quạt tròn và hình vành khuyên

Bài 1. Diện tích hình quạt tròn bán kính R, ứng với cung 45° là

A. $\pi R^2;$

B. $\frac{\pi R^2}{2};$

C. $\frac{\pi R^2}{4};$

D. $\frac{\pi R^2}{8}.$

Hướng dẫn giải

Đáp án đúng là: D

Diện tích hình quạt tròn bán kính R, ứng với cung 45° là:

$S=\frac{\pi R^{2}n}{360}=\frac{\pi .R^2.45}{360}=\frac{\pi R^2}{8}.$

Diện tích hình quạt tròn bán kính R, ứng với cung 45° là $\frac{\pi R^2}{8}.$

Bài 2. Diện tích hình vành khuyên giới hạn bởi đường tròn (O; 1 cm) và (O; 3 cm) là

A. 10 cm²;

B. 8 cm²;

C. 8π cm²;

D. 10π cm².

Hướng dẫn giải

Đáp án đúng là: C

Diện tích hình vành khuyên giới hạn bởi đường tròn (O; 1 cm) và (O; 3 cm) là:

$S=\pi \left(R^2-r^2\right)=\pi \left(3^2-1^2\right)=8\pi$ (cm²).

Bài 3. Cho đường tròn (O; 5 cm).

a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây bằng 2,5 cm;

b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm);

c) Tính số đo và độ dài của cung nhỏ AB;

d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.

Hướng dẫn giải

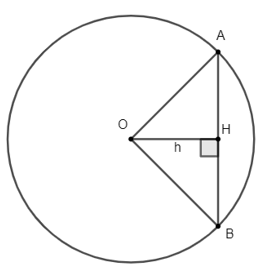
Theo đề bài, ta có hình vẽ sau:

a) Vẽ bán kính OM của đường tròn, trên OM lấy điểm H sao cho OH = 2,5 cm.

Kẻ đoạn thẳng AB vuông góc với OH tại H, cắt đường tròn tại A và B.

Khi đó, ta được dây cung AB cần vẽ.

b) Gọi H là trung điểm của AB.

Xét ∆OAH và ∆OBH có:

OA = OB = R; OH chung; $\widehat{OHA}=\widehat{OHB}=90°$.

Do đó ∆OAH = ∆OBH (cạnh huyền – cạnh góc vuông)

Suy ra AH = BH (hai cạnh tương ứng) và AB = 2AH.

Xét ∆OAH vuông tại H có: AH² + OH² = OA² (định lí Pythagore)

Hay AH² = OA² – OH² = 5² – 2,5² = 18,75.

Suy ra $AH=\frac{5\sqrt{3}}{2}$ (cm) và $AB=2.\frac{5\sqrt{3}}{2}=5\sqrt{3}\approx 8,66$ (cm).

Vậy độ dài của dây AB khoảng 8,66 cm.

c) Xét ∆OAH vuông tại H có:

$\cos \widehat{AOH}=\frac{OH}{OA}=\frac{2,5}{5}=\frac{1}{2}$ suy ra $\widehat{AOH}=60°.$

Mà ∆OAH = ∆OBH suy ra $\widehat{BOH}=\widehat{AOH}=60°$ (hai góc tương ứng)

Suy ra $\widehat{AOB}=\widehat{BOH}+\widehat{AOH}=60°+60°=120°$ và $sđ\stackrel{⏜}{AB}=120°.$

Độ dài cung AB là: $\frac{120}{180}.\pi .5=\frac{10}{3}\pi$ (cm).

Vậy $sđ\stackrel{⏜}{AB}=120°$ và độ dài cung nhỏ AB bằng $\frac{10}{3}\pi cm$ .

d) Diện tích hình quạt tròn ứng với cung nhỏ AB là:

$\frac{\pi .5^2.120}{360}=\frac{25\pi }{3}$ (cm²).

Vậy diện tích hình quạt tròn ứng với cung nhỏ AB bằng $\frac{25\pi }{3}$ cm².

Bài 4. Tính độ dài các cung 60°; 90°; 150° của đường tròn (O; 5 cm) (làm tròn kết quả đến hàng phần trăm).

Hướng dẫn giải

Cung 60°, bán kính R = 5 cm có độ dài là: $\mathcal{l}=\frac{\pi Rn}{180}=\frac{\pi .5.60}{180}=\frac{5\pi }{3}\approx 5,23$ (cm).

Cung 90°, bán kính R = 5 cm có độ dài là: $\mathcal{l}=\frac{\pi Rn}{180}=\frac{\pi \mathrm{.5.90}}{180}=\frac{5\pi }{2}\approx 7,85$ (cm).

Cung 150°, bán kính R = 5 cm có độ dài là: $\mathcal{l}=\frac{\pi Rn}{180}=\frac{\pi \mathrm{.5.60}}{180}=\frac{25\pi }{6}\approx 13,09$