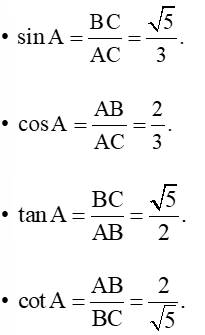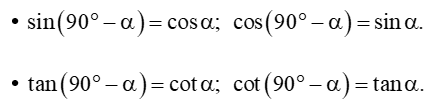Lý thuyết Tỉ số lượng giác của góc nhọn - Toán 9 Chân trời sáng tạo

Lý thuyết Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn

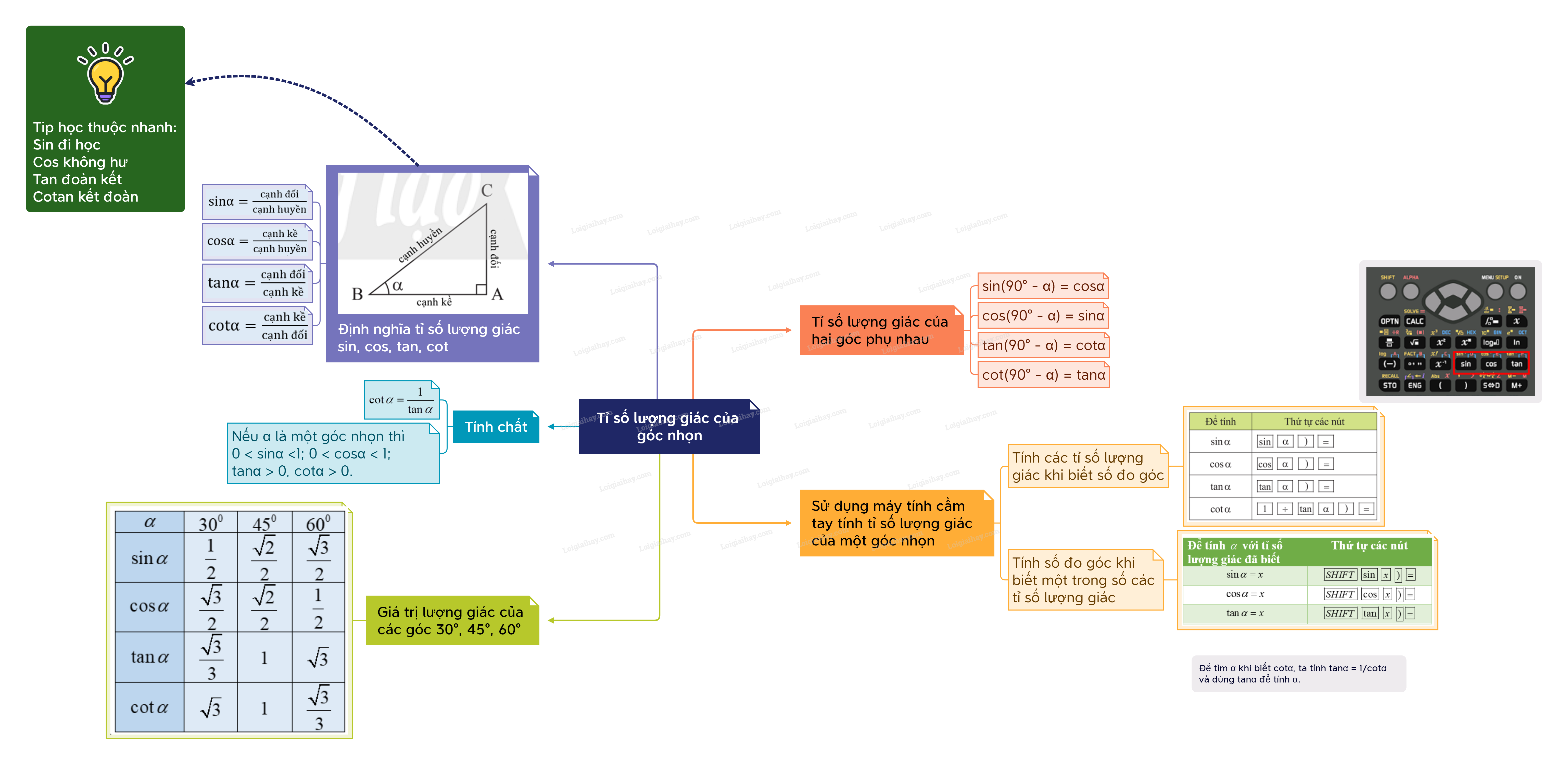
1. Định nghĩa tỉ số lượng giác của góc nhọn

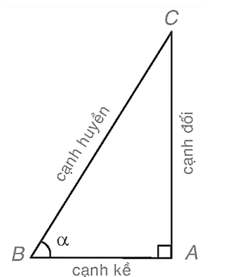
Cho tam giác ABC vuông tại A có góc nhọn B bằng α. Ta gọi AC là cạnh đối của góc α, AB là cạnh kề của góc α.

Xét tam giác ABC vuông tại A có $\widehat{ABC}=\alpha ,$ ta có:

• Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu sin α.

• Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu cos α.

• Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu tan α.

• Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu cot α.

Chú ý: Với góc nhọn α, ta có:

• 0 < sin α < 1; 0 < cos α < 1.

• $\cot \alpha =\frac{1}{\tan \alpha }.$

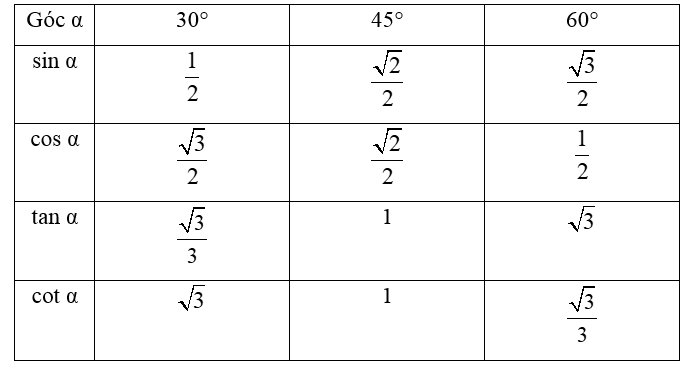
• Ta có bảng tỉ số lượng giác của các góc 30°, 45°, 60° như sau:

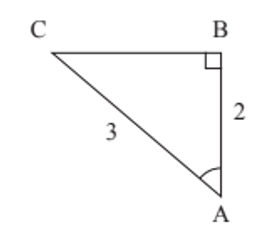
Ví dụ 1: Cho tam giác ABC vuông tại B có AB = 2, AC = 3. Tính các tỉ số lượng giác của góc nhọn A.

Hướng dẫn giải

Theo định lí Pythagore, ta có: AC² = AB² + BC²

Nên BC² = AC² – AB² = 3² − 2² = 5 nên $BC=\sqrt{5}.$

Ta có các tỉ số lượng giác của góc A là:

Vậy $\sin A=\frac{\sqrt{5}}{3},\cos A=\frac{2}{3},\tan A=\frac{\sqrt{5}}{2},\cot A=\frac{2}{\sqrt{5}}.$

Ví dụ 2: Tính giá trị của biểu thức $A=\frac{\sin 60°.\cos 30°}{\cot 45°}.$

Hướng dẫn giải

Ta có: $A=\frac{\sin 60°.\cos 30°}{\cot 45°}=\frac{\frac{\sqrt{3}}{2}.\frac{\sqrt{3}}{2}}{1}=\frac{3}{4}.$

2. Tỉ số lượng giác của hai góc phụ nhau

• Hai góc được gọi là phụ nhau nếu chúng có tổng bằng 90°. Như vậy, góc phụ của góc nhọn α là góc (90° − α).

• Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Chú ý: Khi viết các tỉ số lượng giác của một góc nhọn trong tam giác, ta có thể viết sin A thay cho $\sin \widehat{A}.$

Ví dụ: So sánh:

a) sin 65° và cos 35°;

b) tan 15° và cot 70°.

Hướng dẫn giải

a) Ta có: $\sin 65°=\cos \left(90°-65°\right)=\cos 25°$ mà 25° < 35°.

Suy ra, sin 65° < cos 35°.

b) Ta có: $\tan 15°=\cot \left(90°-15°\right)=\cot 75°$ mà 75° > 70°.

Suy ra, tan 15° > cot 70°.

Sơ đồ tư duy Tỉ số lượng giác của góc nhọn

Bài tập Tỉ số lượng giác của góc nhọn

Bài 1. Cho α là góc nhọn bất kỳ. Chọn khẳng định sai.

A. $\tan \alpha =\frac{\sin \alpha }{\cos \alpha };$

B. $\cot \alpha =\frac{\cos \alpha }{\sin \alpha };$

C. $\tan \alpha .\cot \alpha =1;$

D. ${\tan }^2\alpha -1={\cos }^2\alpha .$

Hướng dẫn giải

Đáp án đúng là: D

Cho α là góc nhọn bất kỳ, khi đó:

• ${\sin }^2\alpha +{\cos }^2\alpha =1;$$\tan \alpha .\cot \alpha =1.$

• $\tan \alpha =\frac{\sin \alpha }{\cos \alpha };$$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }.$

• $1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha };$$1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }.$

Bài 2. Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác của góc B trong mỗi trường hợp sau:

a) BC = 12 cm; AB = 8 cm;

b) $AB=a\sqrt{2};$$AC=2\sqrt{2}a.$

Hướng dẫn giải

a) Theo định lí Pythagore, ta có: BC² = AB² + AC²

Suy ra AC² = BC² – AB² = 12² – 8² = 80.

Do đó $AC=4\sqrt{5}$ cm.

Các tỉ số lượng giác của góc B là:

• $\sin B=\frac{AC}{BC}=\frac{4\sqrt{5}}{12}=\frac{\sqrt{5}}{3};$$\cos B=\frac{AB}{BC}=\frac{8}{12}=\frac{2}{3}.$

• $\tan B=\frac{AC}{AB}=\frac{4\sqrt{5}}{8}=\frac{\sqrt{5}}{2};$$\cot B=\frac{AB}{AC}=\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}.$

Vậy $\sin B=\frac{\sqrt{5}}{3};\cos B=\frac{2}{3};\tan B=\frac{\sqrt{5}}{2};\cot B=\frac{2\sqrt{5}}{5}.$

b) Theo định lí Pythagore, ta có: BC² = AB² + AC²

$={\left(a\sqrt{2}\right)}^2+{\left(2\sqrt{2}a\right)}^2$$=2a^2+8a^2$$=10a^2$

Suy ra $BC=a\sqrt{10}.$

Các tỉ số lượng giác của góc B là:

• $\sin B=\frac{AC}{BC}=\frac{2\sqrt{2}a}{a\sqrt{10}}=\frac{2\sqrt{5}a}{5};$$\cos B=\frac{AB}{BC}=\frac{a\sqrt{2}}{a\sqrt{10}}=\frac{\sqrt{5}}{5}.$

• $\tan B=\frac{AC}{AB}=\frac{2\sqrt{2}a}{a\sqrt{2}}=2;$$\cot B=\frac{1}{\tan B}=\frac{1}{2}.$

Vậy $\sin B=\frac{2\sqrt{5}a}{5};\cos B=\frac{\sqrt{5}}{5};\tan B=2;\cot B=\frac{1}{2}.$

Bài 3. Cho α là góc nhọn bất kỳ. Chọn khẳng định đúng.

A. $\sin \alpha +\cos \alpha =1;$

B. ${\sin }^2\alpha +{\cos }^2\alpha =1;$

C. ${\sin }^3\alpha +{\cos }^3\alpha =1;$

D. $\sin \alpha -\cos \alpha =1.$

Hướng dẫn giải

Đáp án đúng là: B

Cho α là góc nhọn bất kỳ, khi đó ${\sin }^2\alpha +{\cos }^2\alpha =1.$

Bài 4. Rút gọn và tính các biểu thức sau:

a) $A=\sin 15°-\sin 60°+\cos 30°-\cos 75°+5;$

b) $B={\sin }^{2}82°+\cot 24°.\cot 66°+{\cos }^{2}82°.$

Hướng dẫn giải

a) Ta có: $A=\sin 15°-\sin 60°+\cos 30°-\cos 75°+5$

$=\left(\sin 15°-\cos 75°\right)+\left(\cos 30°-\sin 60°\right)+5$

$=\left(\cos 75°-\cos 75°\right)+\left(\cos 30°-\cos 30°\right)+5$

= 0 + 0 + 5 = 5.

b) Ta có: $B={\sin }^{2}82°+\cot 24°.\cot 66°+{\cos }^{2}82°$

$=\left({\sin }^{2}82°+{\cos }^{2}82°\right)+\cot 24°.\cot 66°$

$=1+\tan 66°.\cot 66°$

= 1 + 1 = 2.

Bài 5. Cho tam giác ABC vuông tại A có AC = 10 cm, $\cos A=\frac{1}{2}.$ Tính sinA và độ dài cạnh AB và BC.

Hướng dẫn giải

Ta có: ${\sin }^{2}A+{\cos }^{2}A=1$ suy ra ${\sin }^{2}A=1-{\cos }^{2}A.$

Do đó $\sin A=\sqrt{1-{\cos }^{2}A}.$

• Thay $\cos A=\frac{1}{2},$ ta có: $\sin A=\sqrt{1-{\left(\frac{1}{2}\right)}^2}=\frac{\sqrt{3}}{2}$ (do sin A > 0 vì góc A nhọn).

Ta lại có: $\cos A=\frac{AB}{AC}$ suy ra AB = AC.cos A.

• Thay $\cos A=\frac{1}{2},$ AC = 10 cm, ta có: $AB=10\cdot \frac{1}{2}=5$ (cm).

Mà $\sin A=\frac{BC}{AC}$ suy ra BC = AC.sin A.

• Thay $\sin A=\frac{\sqrt{3}}{2},$ AC = 10 cm, ta có: $BC=10\cdot \frac{\sqrt{3}}{2}=5\sqrt{3}$ (cm)

Vậy $\sin A=\frac{\sqrt{3}}{2},$AB = 5 cm, $BC=5\sqrt{3}$ cm

Trắc nghiệm: Tỉ số lượng giác của góc nhọn

I. Nhận biết

Câu 1. Cho tam giác MNP vuông tại M có góc nhọn P bằng α. Khi đó cosα bằng

A. $\cos \alpha =\frac{MP}{NP}$.

B. $\cos \alpha =\frac{MN}{MP}$.

C. $\cos \alpha =\frac{MN}{NP}$.

D. $\cos \alpha =\frac{MP}{MN}$.

Câu 2. Cho góc nhọn α. Khẳng định nào sau đây đúng?

A. 0 < sinα < 1; 0 < cosα < 1.

B. –1 < sinα < 1; –1 < cosα < 1.

C. –1 < sinα < 0; –1 < cosα < 0.

D. –1 < sinα < 1; –1 < cosα < 1.

Câu 3. Cho β là góc nhọn bất kì. Khẳng định nào sau đây đúng?

A. $\sin \beta =\frac{1}{\tan \beta }$.

B. $\cos \beta =\frac{1}{\tan \beta }$.

C. $cot\beta =\frac{1}{\tan \beta }$.

D. $cot\beta =\frac{1}{\sin \beta }$.

Câu 4. Cho tam giác vuông có góc nhọn α. Khẳng định nào sau đây sai?

A. Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu tan α.

B. Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu sin α.

C. Tỉ số giữa cạnh huyền và cạnh kề được gọi là côsin của góc α, kí hiệu cot α.

D. Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu cos α.

Câu 5. Cho α, β là hai góc phụ nhau. Kết luận nào sau đây đúng?

A. sinα = cotβ.

B. sinα = tanβ.

C. sinα = cosβ.

D. cosα = cotβ.

II. Thông hiểu

Câu 6. Cho tam giác ABC vuông tại A. Trong các khẳng định sau, khẳng định nào đúng?

A. sinB = tanC.

B. tanB = cosC.

C. sinC = cosB.

D. $\frac{AB}{AC}=\frac{\cos C}{\cos B}$.

Câu 7. Cho tam giác ABC vuông tại C có AC = 1 cm, BC = 2 cm. Tỉ số lượng giác sinB, cosB là

A. $\sin B=\frac{\sqrt{5}}{5};\cos B=\frac{2\sqrt{5}}{5}$.

B. $\sin B=\frac{1}{\sqrt{3}};\cos B=\frac{2\sqrt{3}}{3}$.

C. $\sin B=\frac{2\sqrt{5}}{5};\cos B=\frac{\sqrt{5}}{5}$.

D. $\sin B=\frac{1}{2};\cos B=\frac{2}{\sqrt{5}}$.

Câu 8. Cho tam giác ABC vuông tại C có AC = 1,2 cm, AB = 1,5 cm. Tỉ số lượng giác tanB là

A. $\tan B=\frac{4\sqrt{41}}{41}$.

B. $\tan B=\frac{4}{3}$.

C. $\tan B=\frac{3}{4}$.

D. $\tan B=\frac{4}{5}$.

Câu 9. Cho tam giác DEF vuông tại D có DE = $\sqrt{2}$ cm, EF = $\sqrt{10}$ cm. Tỉ số lượng giác cot E là

A. $cotE=\frac{1}{2}$.

B. cotE = 2.

C. $cotE=\frac{\sqrt{5}}{5}$.

D. $cotE=\sqrt{5}$.

III. Vận dụng

Câu 10. Một mảnh vườn hình chữ nhật có chiều dài 30 m, chiều rộng $10\sqrt{3}$ m. Khi đó góc giữa đường chéo và chiều dài của mảnh vườn bằng

A. 30^o

B. 45^o

C. 60^o

D. 75^o