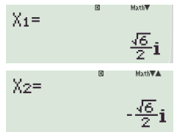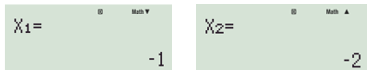Lý thuyết Phương trình bậc hai một ẩn - Toán 9 Chân trời sáng tạo

Lý thuyết Toán 9 Bài 2: Phương trình bậc hai một ẩn

1. Phương trình bậc hai một ẩn

– Phương trình bậc hai một ẩn (còn gọi là phương trình bậc hai) là phương trình có dạng ax² + bx + c = 0, trong đó x là ẩn, a, b, c là những số cho trước gọi là các hệ số và a ≠ 0.

Ví dụ: Phương trình 3x² + 5x + 6 = 0 là phương trình bậc hai một ẩn với các hệ số a, b, c lần lượt là 3, 5, 6.

2. Giải một số phương trình bậc hai dạng đặc biệt

– Để giải các phương trình bậc hai có dạng ax² + bx = 0 hoặc ax² + c = 0 (với a ≠ 0, c < 0), ta có thể đưa phương trình về dạng phương trình tích rồi giải phương trình.

Ví dụ: Để giải phương trình x² – 1 = 0, ta biến đổi như sau:

x² – 1 = 0

(x – 1)(x + 1) = 0

x = 1 hoặc –1.

Để giải phương trình x² + 2x = 0, ta biến đổi như sau:

x² + 2x = 0

x(x + 2) = 0

x = 0 hoặc x = –2.

3. Công thức nghiệm của phương trình bậc hai

Cho phương trình ax² + bx + c = 0 (a ≠ 0) và biệt thức ∆ = b² – 4ac.

• Nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a},x_2=\frac{-b-\sqrt{\Delta }}{2a}$.

• Nếu ∆ = 0 thì phương trình có nghiệm kép $x_1=x_2=\frac{-b}{2a}$.

• Nếu ∆ < 0 thì phương trình vô nghiệm.

Ví dụ: Để giải phương trình x² – 4x + 3 = 0 ta thực hiện các bước như sau:

Xác định các hệ số của phương trình: a = 1, b = –4, c = 3.

Tính giá trị của biệt thức ∆ và xác định số nghiệm của phương trình.

∆ = (­–4)² – 4 . 1 . 3 = 4 > 0 nên phương trình có hai nghiệm phân biệt.

Tính giá trị các nghiệm của phương trình:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-\left(-4\right)+\sqrt{4}}{2.1}=3$;

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-\left(-4\right)-\sqrt{4}}{2.1}=1$.

Đưa ra kết luận phương trình có hai nghiệm phân biệt là x = 3 và x = 1.

4. Tìm nghiệm của phương trình bậc hai một ẩn bằng máy tính cầm tay

– Ta có thể sử dụng máy tính cầm tay để tìm nghiệm của các phương trình bậc hai bằng cách thực hiện các bước sau:

• Ấn nút ON để khởi động máy.

• Ấn nút MODE.

• Ấn nút 5

• Ấn nút 3, nhập các hệ số a, b, c

• Ấn nút = để xem các nghiệm của phương trình.

Chú ý: Nếu các nghiệm của phương trình được hiển thị dưới dạng ai (trong đó a là hệ số như dưới đây) thì phương trình vô nghiệm.

Ví dụ: Giải phương trình x² + 3x + 2 = 0 bằng máy tính cầm tay ta thu được kết quả như sau:

Vậy phương trình có hai nghiệm là x = –1 và x = –2.

5. Giải bài toán bằng cách lập phương trình bậc hai

Để giải bài toán bằng cách lập phương trình bậc hai, ta thực hiện như sau:

• Bước 1: Lập phương trình:

– Chọn ẩn và đặt điều kiện thích hợp cho ẩn.

– Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.

– Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

• Bước 2: Giải phương trình nói trên.

• Bước 3: Kiểm tra các nghiệm tìm được ở Bước 2 có thoả mãn điều kiện của ẩn hay không, rồi trả lời bài toán.

Ví dụ: Một mảnh đất có chiều dài gấp 4 lần chiều rộng và nếu giảm chiều rộng đi 2 m, tăng chiều dài lên gấp đôi thì diện tích mảnh đất đó sẽ tăng thêm 20 m². Tính chiều dài và chiều rộng của mảnh đất.

Hướng dẫn giải

Gọi chiều rộng của mảnh đất là x (m) (điều kiện: x > 2).

Khi đó chiều dài của mảnh đất là: 4x (m).

Diện tích mảnh đất là: x . 4x = 4x² (m²).

Diện tích mảnh đất sau khi giảm chiều rộng 2 m và tăng chiều dài lên gấp đôi là:

8x.(x – 2) (m²) .

Theo bài ra ta có phương trình: 8x(x – 2) – 4x² = 20.

Giải phương trình ta được x = 5 và x = –1.

Đối chiếu với điều kiện ta được x = 5.

Vậy chiều rộng mảnh đất là 5 m và chiều dài mảnh đất là 20 m.

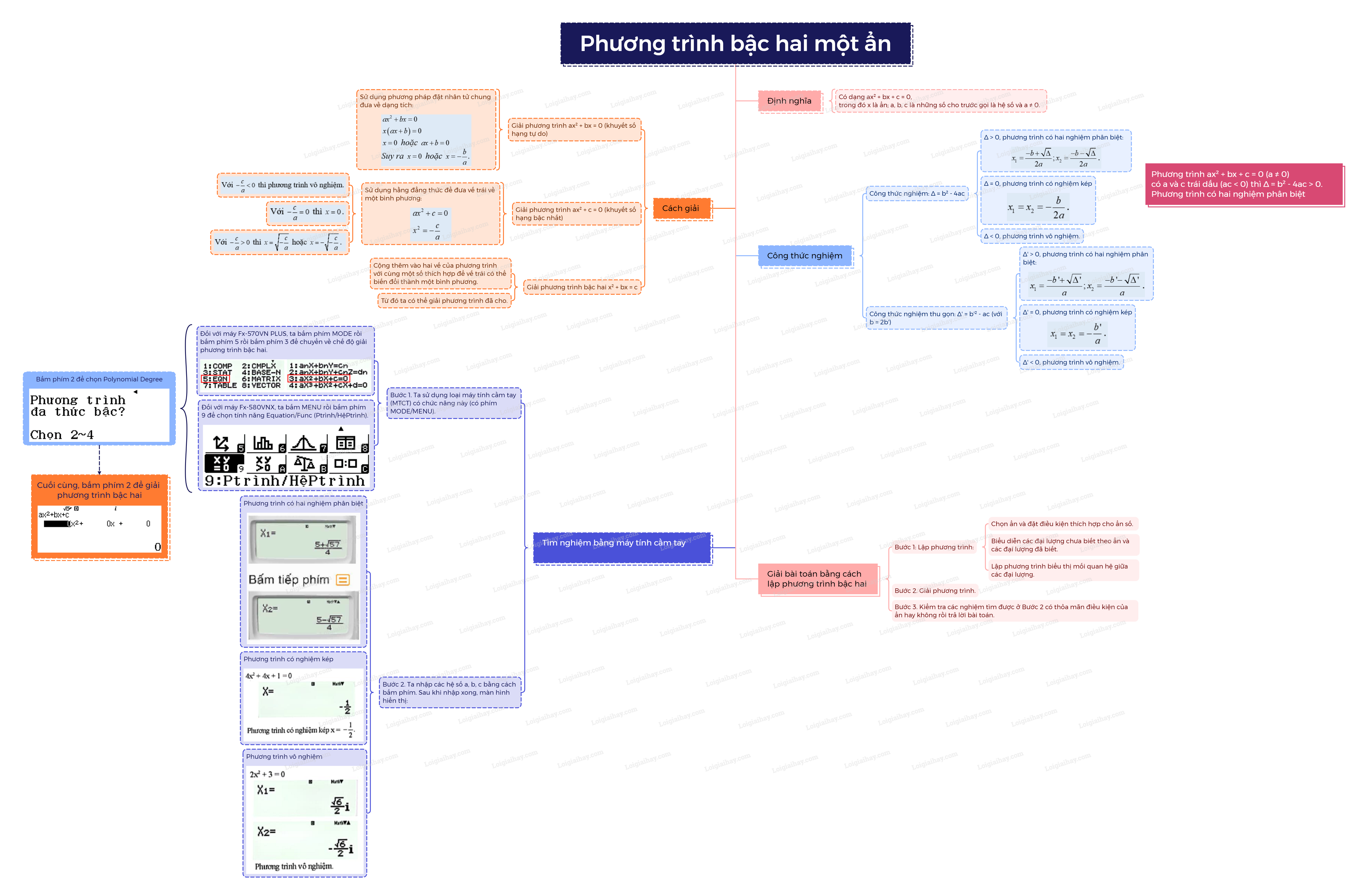
Sơ đồ tư duy Phương trình bậc hai một ẩn

Bài tập Phương trình bậc hai một ẩn

Bài 1. Số nghiệm của phương trình 3x² + 5x – 6 = 0 là

A. 1.

B. 2.

C. Vô nghiệm.

D. Một đáp án khác.

Hướng dẫn giải

Đáp án đúng là: B.

Ta có: ∆ = 5² – 4 . 3 . (–6) = 97 > 0 nên phương trình có 2 nghiệm phân biệt.

Bài 2. Nghiệm dương của phương trình x² + 5x – 6 = 0 là

A. 6.

B. 3.

C. 1.

D. Phương trình không có nghiệm dương.

Hướng dẫn giải

Đáp án đúng là: C.

Ta có: ∆ = 5² – 4 . 1 . (–6) = 49 > 0 nên phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-5+\sqrt{49}}{2.1}=1$;

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-5-\sqrt{49}}{2.1}=-6$.

Vậy nghiệm dương của phương trình là x = 1.

Bài 3. Giải các phương trình sau:

a) x² – x – 11 = 0;

b) –2x² + x – 3 = 0.

Hướng dẫn giải

a) Ta có: ∆ = (–1)² – 4 . 1 . (–11) = 45 > 0 nên phương trình có 2 nghiệm phân biệt.

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-\left(-1\right)+\sqrt{45}}{2.1}=\frac{1+3\sqrt{5}}{2}$;

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-\left(-1\right)-\sqrt{45}}{2.1}=\frac{1-3\sqrt{5}}{2}$.

b) Ta có: ∆ = 1² – 4 . (–2) . (–3) = –23 < 0 nên phương trình vô nghiệm.

Bài 4. Một mảnh đất hình chữ nhật có chu vi bằng 28 m. Đường chéo của hình chữ nhật dài 10 m. Tính chiều dài và chiều rộng của mảnh đất hình chữ nhật đó.

Hướng dẫn giải:

Nửa chu vi của mảnh đất là:

28 : 2 = 14 (m).

Gọi chiều dài của mảnh đất là x (m).

Chiều rộng của mảnh đất là 14 – x (m).

Độ dài đường chéo của mảnh đất là 10 m nên ta có phương trình:

x² + (14 – x)² = 10²

x² + 196 – 28x + x² = 100

2x² – 28x + 96 = 0

Ta có: ∆ = 28² – 4 . 2 . 96 = 16 > 0 nên phương trình có hai nghiệm phân biệt.

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-\left(-28\right)+\sqrt{16}}{2.2}=8$;

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-\left(-28\right)-\sqrt{16}}{2.2}=6$.

• Nếu chiều dài là 8 m thì chiều rộng là 14 – 8 = 6 (m)

• Nếu chiều dài là 6 m thì chiều rộng là 14 – 6 = 8 (m) (loại).

Vậy chiều dài và chiều rộng mảnh đất lần lượt là 8 m và 6 m.