Lý thuyết Đa giác đều và phép quay - Toán 9 Chân trời sáng tạo

Lý thuyết Toán 9 Bài 3: Đa giác đều và phép quay

1. Khái niệm đa giác đều

− Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau được gọi là đa giác đều.

Chú ý:

− Đa giác đều có số cạnh bằng n được gọi là n-giác đều.

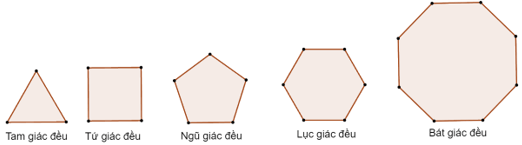
− Với n lần lượt bằng 3, 4, 5, 6, 8 … ta có tam giác đều, tứ giác đều (hình vuông), ngũ giác đều, lục giác đều, bát giác đều,…

− Khi nói đến đa giác đều mà không chú thích gì thêm, ta hiểu đó là đa giác lồi.

− Người ta chứng minh được, với mỗi đa giác đều có đúng một điểm I cách đều tất cả các đỉnh của đa giác. Điểm I gọi là tâm của đa giác đó.

Ví dụ: Dưới đây là một số đa giác đều thường gặp:

2. Phép quay

− Phép quay thuận chiều α° (0° < α° < 360°) tâm O giữ nguyên điểm O, biến điểm M khác điểm O thành điểm M' thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM' thì điểm M tạo nên cung MM' có số đo α°.

− Định nghĩa tương tự cho phép quay ngược chiều α° tâm O.

− Phép quay 0° hay 360° giữ nguyên mọi điềm.

Chú ý:

− Ta coi mỗi phép quay tâm O biến O thành chính nó.

− Nếu một phép quay biến các điểm M trên hình a thành các điểm M' thì các điểm M' tạo thành hình a'. Khi đó, ta nói phép quay biến hình a thành hình a'. Nếu hình a' trùng với hình a thì ta nói phép quay biến hình a thành chính nó.

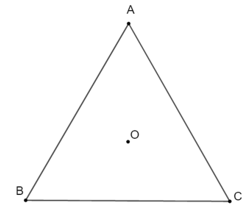
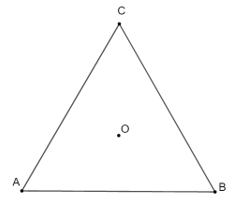
Ví dụ: Cho tam giác đều ABC tâm O như hình dưới đây:

Phép quay biến điểm A thành điểm C sẽ biến các điểm C, B tương ứng thành các điểm B, A như hình dưới đây:

Đây là phép quay thuận chiều 120° tâm O hoặc phép quay ngược chiều 240° tâm O.

3. Hình phẳng đều trong thực tế

− Tương tự như các đa giác đều, trong tự nhiên, sản xuất, thiết kế, … cũng có các hình phẳng đều.

Ví dụ: Dưới đây là một số đa giác đều trong thực tế:

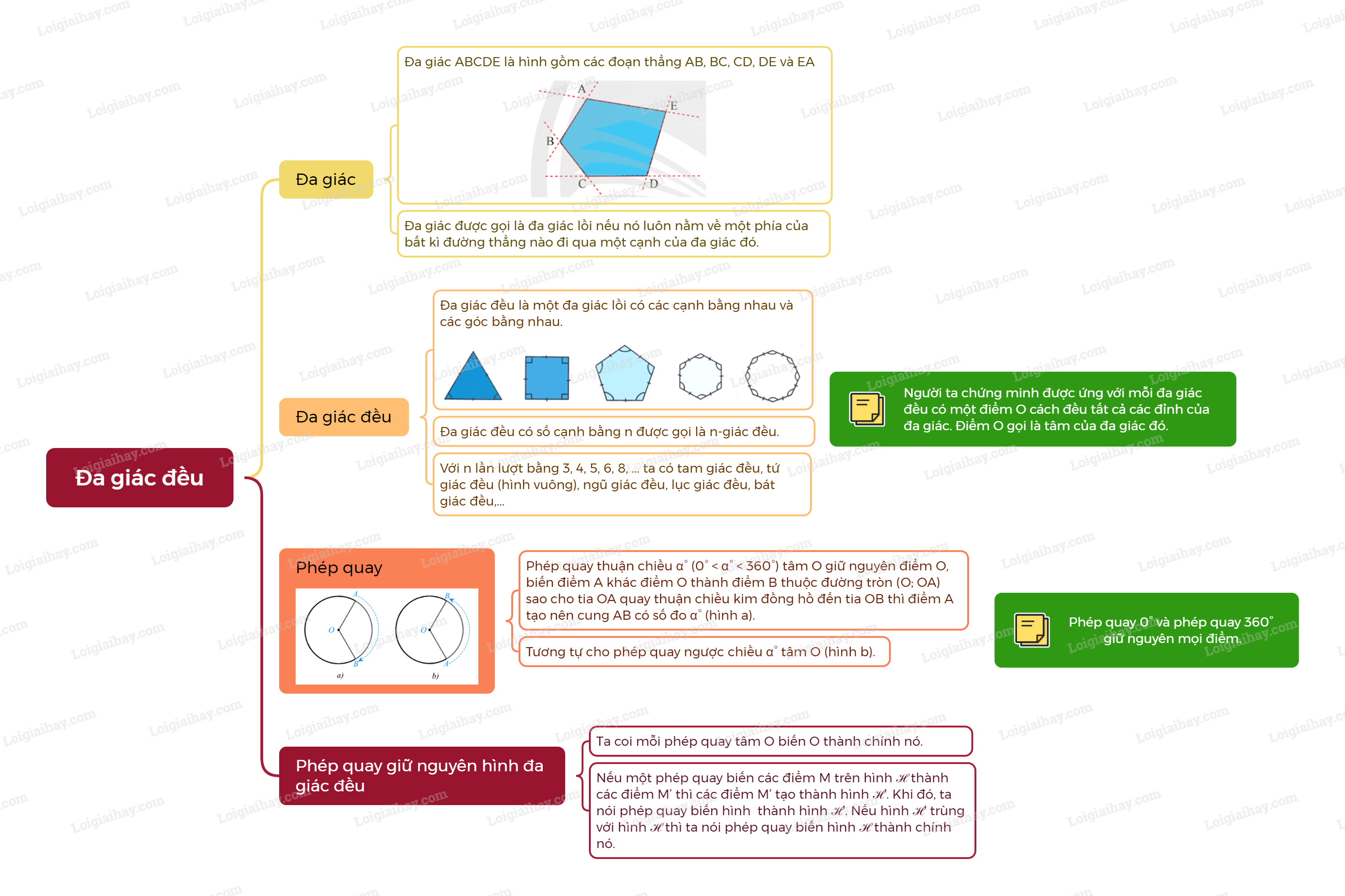
Sơ đồ tư duy Đa giác đều và phép quay

Bài tập Đa giác đều và phép quay

Bài 1. Số đo của mỗi góc của ngũ giác đều là

A. 100°.

B. 108°.

C. 110°.

D. 120°.

Hướng dẫn giải

Đáp án đúng là: B

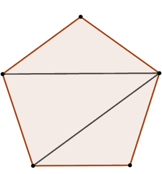
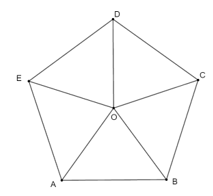
Chia ngũ giác đều thành 3 tam giác như hình trên.

Mỗi góc của ngũ giác đều bằng: $\frac{3.180}{5}=108°$.

Bài 2. Ssố cạnh của một đa giác đều, biết mỗi góc của nó bằng 135° là

A. 5.

B. 6.

C. 7.

D. 8.

Hướng dẫn giải

Đáp án đúng là: D

Gọi n là số cạnh của đa giác đều.

Từ đa giác đều ta chia được n – 2 tam giác.

Số đo mỗi góc của đa giác đều là: $\frac{\left(n-2\right).180°}{n}=135°$ nên $n=8$ .

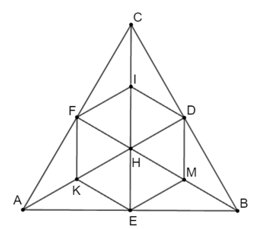
Bài 3. Cho tam giác đều ABC, các đường cao AD , BE , CF cắt nhau tại H. Gọi I , K , M theo thứ tự là trung điểm của HA, HB, HC. Chứng minh rằng DKFIEM là lục giác đều.

Hướng dẫn giải

Xét ∆HDC vuông tại D, DM là đường trung tuyến ứng với cạnh huyền nên DM = HM.

Ta lại có $\widehat{C_1}=30°$ nên $\widehat{H_1}=60°$.

Do đó HDM∆ là tam giác đều.

Tương tự các tam giác HME, HEI, HIF, HFK, HKD là các tam giác đều.

Lục giác DKFIEM có các cạnh bằng nhau và các góc bằng nhau (bằng 120° ) nên là lục giác đều.

Bài 4.

a) Tính số đường chéo của đa giác n cạnh.

b) Đa giác nào có số đường chéo bằng số cạnh?

Hướng dẫn giải

a) Từ mỗi đỉnh của hình n – giác lồi, kẻ được n − 1 đoạn thẳng đến các đỉnh còn lại, trong đó có hai đoạn thẳng là cạnh của đa giác, n − 3 đoạn thẳng là đường chéo.

Đa giác có n đỉnh nên kẻ được n(n – 3) đường chéo, trong đó mỗi đường chéo tính 2 lần. Vậy số đường chéo của hình n − giác lồi là $\frac{n\left(n-3\right)}{2}$.

b) Ta có $\frac{n\left(n-3\right)}{2}=n$ nên $n=5$.

Vậy ngũ giác có số đường chéo bằng số cạnh.

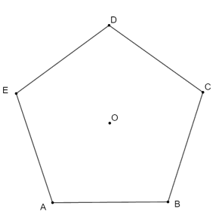
Bài 5. Cho hình ngũ giác đều ABCDE tâm O.

a) Phép quay thuận chiều tâm O biến điểm A thành điểm E thì các điểm B, C, D, E tương ứng biến thành các điểm nào?

b) Phép quay ngược chiều tâm O biến điểm A thành điểm C thì các điểm B, C, D, E tương ứng biến thành các điểm nào?

c) Chỉ ra các phép quay tâm O giữ nguyên hình ngũ giác đều.

Hướng dẫn giải

a) Phép quay thuận chiều tâm O biến điểm A thành điểm E thì các điểm B, C, D, E tương ứng biến thành các điểm A, B, C, D.

b) Phép quay ngược chiều tâm O biến điểm A thành điểm C thì các điểm B, C, D, E tương ứng biến thành các điểm D, E, A, B.

c)

Ta có $\widehat{DOC}=\widehat{COB}=\widehat{BOA}=\widehat{AOE}=\widehat{EOD}=\frac{360}{5}=72°$.

Vậy các phép quay giữ nguyên hình ngũ giác đều là phép quay thuận chiều tâm O một góc 72°, 144°, 216°, 288°, 360° và phép quay ngược chiều tâm O một góc 72°, 144°, 216°, 288°, 360°.