Nội dung bài viết

    Xem thêm

    Lý thuyết Hàm số và đồ thị của hàm số y = ax^2 (a ≠ 0) - Toán 9 Chân trời sáng tạo

    Tóm tắt lý thuyết Toán lớp 9 Bài 1: Hàm số và đồ thị của hàm số y = ax2 (a ≠ 0) hay, chi tiết sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 9.

    1 79 12/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Lý thuyết Toán 9 Bài 1: Hàm số và đồ thị của hàm số y = ax2 (a ≠ 0)

    1. Hàm số y = ax2 (a ≠ 0)

    – Hàm số y = ax2 (a ≠ 0) xác định với mọi giá trị x∈ℝ nên tập xác định của hàm số là D=ℝ.

    Ví dụ: Các hàm số sau đây có dạng y = ax2 (a ≠ 0): y = 5x2; y = –3x2; y=13x2 ; …

    2. Bảng giá trị của hàm số y = ax2 (a ≠ 0)

    Để lập bảng giá trị của hàm số y = ax2 (a ≠ 0), ta lần lượt cho x nhận các giá trị x1, x2, x3,... (x1, x2, x3,... tăng dần) và tính các giá trị tương ứng của y rồi ghi vào bảng như sau:

    x

    x1

    x2

    x3

    …

    y = ax2

    y1

    y2

    y3

    …

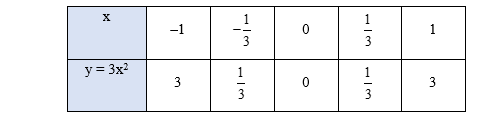
    Ví dụ: Dưới đây là bảng giá trị của hàm số y = 3x2 với các giá trị x lần lượt bằng –3; –2; –1; 0; 1; 2; 3:

    x

    –3

    –2

    –1

    0

    1

    2

    3

    y = 3x2

    27

    12

    3

    0

    3

    12

    27

    3. Đồ thị của hàm số y = ax2 (a ≠ 0)

    Đồ thị của hàm số số y = ax2 (a ≠ 0) là một đường cong đi qua gốc toạ độ, nhận trục tung làm trục đối xứng. Đường cong đó được gọi là một parabol đỉnh O.

    • Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.

    • Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.

    Chú ý: Để vẽ đồ thị hàm số y = ax2 (a ≠ 0), ta thực hiện các bước sau:

    – Lập bảng giá trị của hàm số với một số giá trị của x (thường lấy 5 giá trị gồm 0 và hai cặp giá trị đối nhau).

    – Trên mặt phẳng tọa độ Oxy, đánh dấu các điểm (x; y) trong bảng giá trị (gồm điểm (0; 0) và hai cặp điểm đối xứng nhau qua trục Oy).

    – Vẽ đường parabol đi qua các điểm vừa được đánh dấu.

    Vì đồ thị của hàm số y = ax2 (a ≠ 0) luôn đi qua gốc toạ độ O và nhận trục Oy làm trục đối xứng nên khi vẽ đồ thị hàm số, ta chỉ cần tìm một số điểm bên phái trục Oy rồi lấy các điểm đối xứng với chúng qua trục Oy.

    Ví dụ: Để vẽ đồ thị của hàm số y = 2x2 ta lập bảng giá trị của hàm số:

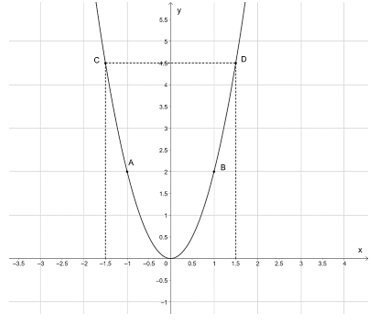
    Trên mặt phẳng tọa độ Oxy, lấy các điểm A(–1; 2); B(1; 2); O(0; 0); C(–1,5; 4,5); D(1,5; 4,5).

    Đồ thị của hàm số y = 2x2 là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như sau:

    Hàm số và đồ thị của hàm số y = ax^2 (a ≠ 0) (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

    Sơ đồ tư duy Hàm số và đồ thị của hàm số y = ax2 (a ≠ 0)

    Lý thuyết Hàm số và đồ thị của hàm số y = ax^2 (a ≠ 0) - Toán 9 Chân trời sáng tạo (ảnh 1)

    Bài tập Hàm số và đồ thị của hàm số y = ax2 (a ≠ 0)

    Bài 1. Trong các hàm số sau, đồ thị hàm số nào nằm dưới trục hoành?

    A. y = x2.

    B. y = 2x2.

    C. y=12x2.

    D. y = –x2.

    Hướng dẫn giải:

    Đáp án đúng là: D

    Đồ thị hàm số y = –x2 nằm dưới trục hoành vì a = –1 < 0.

    Bài 2. Điểm cao nhất của đồ thị của hàm số số y = ax2 (a < 0) có hoành độ là

    A. –1.

    B. 0.

    C. 1.

    D. 2.

    Hướng dẫn giải:

    Đáp án đúng là: B

    Khi a < 0 thì đồ thị của hàm số số y = ax2 nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị. Tọa độ của điểm O là (0; 0).

    Bài 3. Lập bảng giá trị của hàm số y=13x2 với các giá trị x lần lượt bằng –2; –1; 2; 5; 8

    Hướng dẫn giải

    Bảng giá trị của hàm số y=13x2:

    Hàm số và đồ thị của hàm số y = ax^2 (a ≠ 0) (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

    Bài 4. Vẽ đồ thị của hàm số y = 3x2.

    Hướng dẫn giải

    Bảng giá trị của hàm số:

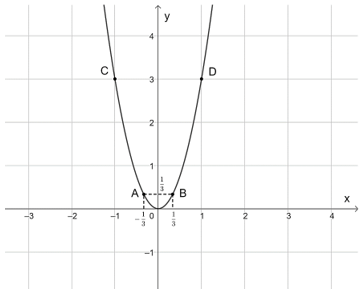
    Hàm số và đồ thị của hàm số y = ax^2 (a ≠ 0) (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

    Trên mặt phẳng tọa độ Oxy, lấy các điểm A−13;13; B13;13; O(0; 0); C(–1; 3); D(1; 3).

    Đồ thị của hàm số y = 3x2 là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như sau:

    Hàm số và đồ thị của hàm số y = ax^2 (a ≠ 0) (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

    Bài 5. Vẽ đồ thị của hàm số y=−13x2.

    Hướng dẫn giải

    Bảng giá trị của hàm số:

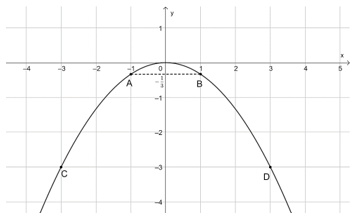
    Hàm số và đồ thị của hàm số y = ax^2 (a ≠ 0) (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

    Trên mặt phẳng tọa độ Oxy, lấy các điểm A−1;−13; B1;−13; O(0; 0); C(–3; –3); D(3; –3).

    Đồ thị của hàm số y=−13x2 là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như sau:

    Hàm số và đồ thị của hàm số y = ax^2 (a ≠ 0) (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

    Bài 6. Viết công thức tính diện tích của hình vuông cạnh 2a. Lập bảng giá trị diện tích của hình lập phương với các giá trị a lần lượt là 1; 2; 3.

    Hướng dẫn giải

    Diện tích hình vuông là S=2a2=4a2.

    Bảng giá trị của hàm số:

    Hàm số và đồ thị của hàm số y = ax^2 (a ≠ 0) (Lý thuyết Toán lớp 9) | Chân trời sáng tạo

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 79 12/10/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: