Gọi A là tập nghiệm của đa thức P(x), B là tập nghiệm của đa thức Q(x), C là tập nghiệm

Lời giải Bài 25 trang 14 SBT Toán 10 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

1 3,422 27/10/2024

Trang trước

Trang sau

Giải SBT Toán 10 Cánh diều Bài 2: Tập hợp. Các phép toán trên tập hợp

Bài 25 trang 14 SBT Toán 10 Tập 1: Gọi A là tập nghiệm của đa thức P(x), B là tập nghiệm của đa thức Q(x), C là tập nghiệm của đa thức P(x).Q(x). C là tập hợp nào sau đây?

A. A∪B;

B. A∩B;

C. A\B;

D. B\A.

Đáp án đúng là A

* Lời giải:

Xét P(x).Q(x) = 0

⇔ $[\begin{array}{l} P (x) = 0 \\ Q (x) = 0 \end{array}$

Do đó nghiệm của đa thức P(x).Q(x) là nghiệm của đa thức P(x) hoặc đa thức Q(x) nên C = A∪B.

* Phương pháp giải:

Ta có C là tập nghiệm của đa thức P(x).Q(x) nên nghiệm của cả 2 đa thức A và B sẽ là nghiệm của đa thức C

* Lý thuyết cần nắm thêm về tập hợp và các phép toán trên tập hợp:

Các khái niệm cơ bản về tập hợp

1.Tập hợp

• Có thể mô tả một tập hợp bằng một trong hai cách sau:

Cách 1. Liệt kê các phần tử của tập hợp;

Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

a ∈ S: phần tử a thuộc tập hợp S.
a ∉ S: phần tử a không thuộc tập hợp S.

Chú ý: Số phần tử của tập hợp S được kí hiệu là n(S).

2. Tập hợp con

• Nếu mọi phần tử của tập hợp T đều là phần tử của tập hợp S thì ta nói T là một tập hợp con (tập con) của S và viết là T ⊂ S (đọc là T chứa trong S hoặc T là tập con của S).

- Thay cho T ⊂ S, ta còn viết S ⊃ T (đọc là S chứa T).

- Kí hiệu T ⊄ S để chỉ T không là tập con của S.

Nhận xét:

- Từ định nghĩa trên, T là tập con của S nếu mệnh đề sau đúng:

∀ x, x ∈ T ⇒ x ∈ S.

- Quy ước tập rỗng là tập con của mọi tập hợp.

• Người ta thường minh họa một tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven.

Tài liệu VietJack

Minh họa T là một tập con của S như sau:

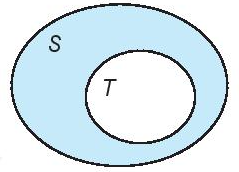
Tài liệu VietJack

Các tập hợp số

1. Mối quan hệ giữa các tập hợp số

- Tập hợp các số tự nhiên ℕ = {0; 1; 2; 3; 4; ....}.

- Tập hợp các số nguyên ℤ gồm các số tự nhiên và số nguyên âm:

ℤ = {...; – 3; – 2; – 1; 0; 1; 2; 3}.

- Tập hợp các số hữu tỉ ℚ gồm các số được viết dưới dạng phân số $\frac{a}{b}$ , với a, b ∈ ℤ, b ≠ 0.

Số hữu tỉ còn được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

- Tập hợp các số thực ℝ gồm các số hữu tỉ và các số vô tỉ. Số vô tỉ là các số thập phân vô hạn không tuần hoàn.

- Mối quan hệ giữa các tập hợp số: ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ.

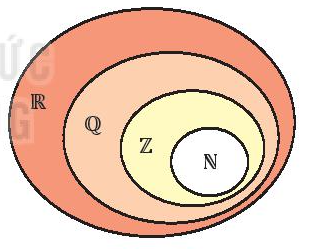
Tài liệu VietJack

2. Các tập con thường dùng của ℝ

- Một số tập con thường dùng của tập số thực ℝ:

+ Khoảng:

$(a; b) = \{x \in ℝ | a < x < b\}$

Tài liệu VietJack

$(a; + \infty) = \{a \in ℝ | x > a\}$

Tài liệu VietJack

$(- \infty; b) = \{x \in ℝ | x < b\}$

Tài liệu VietJack

$(- \infty; + \infty)$

Tài liệu VietJack

+ Đoạn

$[a; b] = \{x \in ℝ | a \leq x \leq b\}$

Tài liệu VietJack

+ Nửa khoảng

$[a; b) = \{x \in ℝ | a \leq x < b\}$

Tài liệu VietJack

$(a; b] = \{x \in ℝ | a < x \leq b\}$

Tài liệu VietJack

$[a; + \infty) = \{x \in ℝ | x \geq a\}$

Tài liệu VietJack

$(- \infty; b] = \{x \in ℝ | x \leq b\}$

Tài liệu VietJack

- Kí hiệu + ∞: Đọc là dương vô cực (hoặc dương vô cùng).

- Kí hiệu – ∞: Đọc là âm vô cực (hoặc âm vô cùng).

- a, b gọi là các đầu mút của đoạn, khoảng hay nửa khoảng.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Tập hợp và các phép toán trên tập hợp - Toán 10

Giải Toán 10 Bài 2 (Cánh diều): Tập hợp. Các phép toán trên tập hợp

Trắc nghiệm Toán 10 Cánh diều Bài 2. Tập hợp. Các phép toán trên tập hợp (phần 2) có đáp án

Bài 18 trang 14 SBT Toán 10 Tập 1: Cho tập hợp A = {x ∈ ℕ| x ≤ 4}. A là tập hợp nào sau đây?...

Bài 19 trang 14 SBT Toán 10 Tập 1: Cho tập hợp A = {0; 1; 2; 3; 4}, B = {3; 4; 5; 6}. Tập hợp ...

Bài 20 trang 14 SBT Toán 10 Tập 1: Cho tập hợp A = {0; 1; 2; 3; 4}, B = {3; 4; 5; 6}. Tập hợp ...

Bài 21 trang 14 SBT Toán 10 Tập 1: Cho hai tập hợp A = (– 3; 3], B = ( – 2; +∞). Tập hợp A∩B ...

Bài 22 trang 14 SBT Toán 10 Tập 1: Cho tập hợp A = {x ∈ ℝ| x ≥ 2, x ≠ 5}. A là tập hợp nào ...

Bài 23 trang 14 SBT Toán 10 Tập 1: Cho hai tập hợp A = {x ∈ ℝ| – 2 ≤ x ≤ 5}, B = {x ∈ ℤ | x² ...

Bài 24 trang 14 SBT Toán 10 Tập 1: Cho hai tập hợp A = [– 1; +∞). Tập hợp C_ℝA bằng:...

Bài 25 trang 14 SBT Toán 10 Tập 1: Gọi A là tập nghiệm của đa thức P(x), B là tập nghiệm của ...

Bài 26 trang 14 SBT Toán 10 Tập 1: Gọi A là tập nghiệm của đa thức P(x), B là tập nghiệm của ...

Bài 27 trang 14 SBT Toán 10 Tập 1: Cho tập hợp X = {a; b; c; d}. Viết tất cả các tập hợp con có ba phần tử của tập hợp X....

Bài 28 trang 14 SBT Toán 10 Tập 1: Cho ba tập hợp: A là tập hợp các tam giác; B là tập hợp ...

Bài 29 trang 14 SBT Toán 10 Tập 1: Dùng kí hiệu ⊂ để mô tả mối quan hệ của hai tập hợp khác ...

Bài 30 trang 15 SBT Toán 10 Tập 1: Cho ba tập hợp sau: A = {x ∈ ℕ| x ⋮ 2}, B = {x ∈ ℕ| x ⋮ 3},...

Bài 31 trang 15 SBT Toán 10 Tập 1: Xác định các tập hợp sau:...

Bài 32 trang 15 SBT Toán 10 Tập 1: Cho A là một tập hợp. Xác định các tập hợp sau:...

Bài 33 trang 15 SBT Toán 10 Tập 1: Cho các tập hợp A. Có nhận xét gì về tập hợp B nếu:...

Bài 34 trang 15 SBT Toán 10 Tập 1: Trong đợt văn nghệ chào mừng ngày 20/11, lớp 10A đăng ...

Bài 35 trang 15 SBT Toán 10 Tập 1: Lớp 10A có 27 học sinh tham gia ít nhất một trong hai câu ...

Bài 36 trang 15 SBT Toán 10 Tập 1: Tìm tập hợp D = E ∩ G, biết E và G lần lượt là tập nghiệm ...

Bài 37 trang 15 SBT Toán 10 Tập 1: Cho các tập hợp: A = [– 1; 7], B = (m – 1; m + 5) với m là ...

Bài 38 trang 16 SBT Toán 10 Tập 1: Cho A = [m; m + 2] và B = [n; n + 1] với m, n là các tham ...

Bài 39 trang 16 SBT Toán 10 Tập 1: Cho A = (– ∞; m + 1), B = [3; +∞) với m là một tham số ...

Bài 40 trang 16 SBT Toán 10 Tập 1: Biểu diễn tập hợp A = {x ∈ ℝ| x² ≥ 9} thành hợp các nửa ...

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 1: Mệnh đề toán học

Bài ôn tập chương 1

Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài ôn tập chương 2

1 3,422 27/10/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: