Nội dung bài viết

    Xem thêm

    Giải Toán 12 trang 85 Tập 1 Chân trời sáng tạo

    Với giải bài tập Toán 12 trang 85 Tập 1 trong Bài tập cuối chương 3 trang 85 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 12 trang 85 Tập 1.

    1 172 17/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 trang 85 Tập 1

    Bài 3 trang 85 Toán 12 Tập 1: Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần tập luyện giải khối rubik 3 × 3, bạn Dũng đã tự thống kê lại thời gian giải rubik trong 25 lần giải liên tiếp ở bảng sau:

    Thời gian giải rubik (giây)

    [8; 10)

    [10; 12)

    [12; 14)

    [14; 16)

    [16; 18)

    Số lần

    4

    6

    8

    4

    3

    a) Khoảng biến thiên của mẫu số liệu ghép nhóm nhận giá trị nào trong các giá trị dưới đây?

    A. 6.

    B. 8.

    C. 10.

    D. 12.

    b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là

    A. 10,75.

    B. 1,75.

    C. 3,63.

    D. 14,38.

    c) Độ lệch chuẩn của mẫu số liệu ghép nhóm có giá trị gần nhất với giá trị nào dưới đây?

    A. 5,98.

    B. 6.

    C. 2,44.

    D. 2,5.

    Lời giải:

    a) Đáp án đúng là: C

    Khoảng biến thiên của mẫu số liệu ghép nhóm là:

    R = 18 – 8 = 10 (giây).

    b) Đáp án đúng là: C

    Cỡ mẫu n = 25.

    Gọi x1; x2; …; x25 là mẫu số liệu gốc về thời gian giải rubik trong 25 lần giải liên tiếp được xếp theo thứ tự không giảm.

    Ta có x1; …; x4 ∈ [8; 10), x5; …; x10 ∈ [10; 12), x11; …; x18 ∈ [12; 14),

       x19; …; x22 ∈ [14; 16), x23; …; x25 ∈ [16; 18).

    Tứ phân vị thứ nhất của mẫu số liệu gốc là 12 (x6 + x7) ∈ [10; 12).

    Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

    Q1 = 10 + 254−46.(12-10) = 10,75.

    Tứ phân vị thứ ba của mẫu số liệu gốc là 12 (x19 + x20) ∈ [14; 16).

    Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

    Q3 = 14 + 3⋅254−4+6+84.(16-14) = 14,375.

    Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

    ∆Q = Q3 – Q1 = 14,375 – 10,75 = 3,625 ≈ 3,63.

    c) Đáp án đúng là: C

    Ta có bảng sau:

    Thời gian giải rubik (giây)

    [8; 10)

    [10; 12)

    [12; 14)

    [14; 16)

    [16; 18)

    Giá trị đại điện

    9

    11

    13

    15

    17

    Số lần

    4

    6

    8

    4

    3

    Số trung bình của mẫu số liệu ghép nhóm là:

    x¯=4⋅9+6⋅11+8⋅13+4⋅15+3⋅1725=12,68.

    Phương sai của mẫu số liệu ghép nhóm là:

    S2 = 125 (4 ∙ 92 + 6 ∙ 112 + 8 ∙ 132 + 4 ∙ 152 + 3 ∙ 172) – (12,68)2 = 5,9776.

    Độ lệch chuẩn của mẫu số liệu ghép nhóm là:

    S=S2=5,9776≈2,44.

    Bài tập tự luận

    Bài 4 trang 85 Toán 12 Tập 1: Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) bác đã lái xe mỗi ngày trong một tháng ở bảng sau:

    Độ dài quãng đường (km)

    [50; 100)

    [100; 150)

    [150; 200)

    [200; 250)

    [250; 300)

    Số ngày

    5

    10

    9

    4

    2

    Hãy xác định khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu trên.

    Lời giải:

    Khoảng biến thiên của mẫu số liệu ghép nhóm là:

    R = 300 – 50 = 250 (km).

    Cỡ mẫu n = 5 + 10 + 9 + 4 + 2 = 30.

    Gọi x1; x2; …; x30 là mẫu số liệu gốc về độ dài quãng đường bác tài xế đã lái xe mỗi ngày trong một tháng được xếp theo thứ tự không giảm.

    Ta có x1; …; x5 ∈ [50; 100), x6; …; x15 ∈ [100; 150), x16; …; x24 ∈ [150; 200),

       x25; …; x28 ∈ [200; 250), x29; x30 ∈ [250; 300).

    Tứ phân vị thứ nhất của mẫu số liệu gốc là x8 ∈ [100; 150).

    Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

    Q1 = 100 + 304−510.(150-100) = 112,5.

    Tứ phân vị thứ ba của mẫu số liệu gốc là x23 ∈ [150; 200).

    Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

    Q3 = 150 +3⋅304−5+109.(200-150) = 5753.

    Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

    ∆Q = Q3 – Q1 = 5753 – 112,5 = ≈ 79,17.

    Ta có bảng sau:

    Độ dài quãng đường (km)

    [50; 100)

    [100; 150)

    [150; 200)

    [200; 250)

    [250; 300)

    Giá trị đại diện

    75

    125

    175

    225

    275

    Số ngày

    5

    10

    9

    4

    2

    Số trung bình của mẫu số liệu ghép nhóm là:

    x¯=5⋅75+10⋅125+9⋅175+4⋅225+2⋅27530=155.

    Phương sai của mẫu số liệu ghép nhóm là:

    S2 = 130 (5 ∙ 752 + 10 ∙ 1252 + 9 ∙ 1752 + 4 ∙ 2252 + 2 ∙ 2752) – 1552 = 3 100.

    Độ lệch chuẩn của mẫu số liệu ghép nhóm là:

    S=S2=3100=1031≈55,68.

    Bài 5 trang 85 Toán 12 Tập 1: Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:

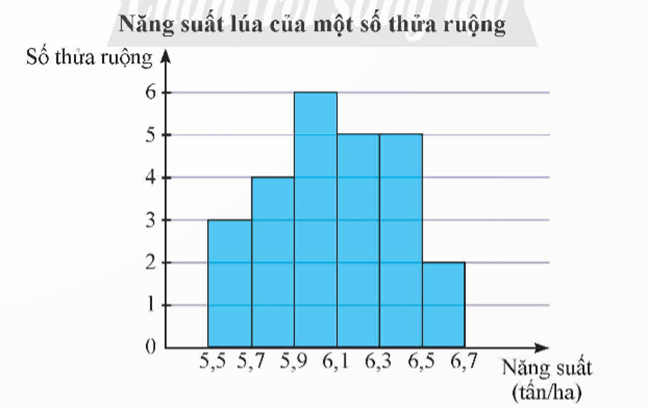
    Bài 5 trang 85 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    a) Có bao nhiêu thửa ruộng đã được khảo sát?

    b) Lập bảng tần số ghép nhóm và tần số tương đối ghép nhóm tương ứng của mẫu số liệu trên.

    c) Hãy xác định khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu trên.

    Lời giải:

    a) Số thửa ruộng được khảo sát là: n = 3 + 4 + 6 + 5 + 5 + 2 = 25.

    b) Từ biểu đồ, ta có bảng tần số ghép nhóm của mẫu số liệu như sau:

    Năng suất (tấn/ha)

    [5,5; 5,7)

    [5,7; 5,9)

    [5,9; 6,1)

    [6,1; 6,3)

    [6,3; 6,5)

    [6,5; 6,7)

    Số thửa ruộng

    3

    4

    6

    5

    5

    2

    Bảng tần số tương đối ghép nhóm của mẫu số liệu:

    Giá trị đại diện (tấn/ha)

    5,6

    5,8

    6,0

    6,2

    6,4

    6,6

    Tần số tương đối

    3

    4

    6

    5

    5

    2

    c) Khoảng biến thiên của mẫu số liệu đã cho là:

    R = 6,7 – 5,5 = 1,2 (tấn/ha).

    Cỡ mẫu n = 25.

    Gọi x1; x2; …; x25 là mẫu số liệu gốc về năng suất của một số thửa ruộng được khảo sát được xếp theo thứ tự không giảm.

    Ta có x1; x2; x3 ∈ [5,5; 5,7), x4; …; x7 ∈ [5,7; 5,9), x8; …; x13 ∈ [5,9; 6,1),

       x13; …; x18 ∈ [6,1; 6,3), x19; …; x23 ∈ [6,3; 6,5), x24; x25 ∈ [6,5; 6,7).

    Tứ phân vị thứ nhất của mẫu số liệu gốc là 12 (x6 + x7) ∈ [5,7; 5,9).

    Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

    Q1 = 5,7 + 254−34.(5,9-5,7) = 5,8625.

    Tứ phân vị thứ ba của mẫu số liệu gốc là 12 (x19 + x20) ∈ [6,3; 6,5).

    Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

    Q3 = 6,3 + 3⋅254−3+4+6+55.(6,5-6,3) = 6,33.

    Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

    ∆Q = Q3 – Q1 = 6,33 – 5,8625 = 0,4675.

    Số trung bình của mẫu số liệu ghép nhóm là:

    x¯=3⋅5,6+4⋅5,8+6⋅6,0+5⋅6,2+5⋅6,4+2⋅6,625=6,088.

    Phương sai của mẫu số liệu ghép nhóm là:

    S2 = 125 [3 ∙ (5,6)2 + 4 ∙ (5,8)2 + 6 ∙ (6,0)2 + 5 ∙ (6,2)2 + 5 ∙ (6,4)2 + 2 ∙ (6,6)2] – (6,088)2

    = 0,086656.

    Độ lệch chuẩn của mẫu số liệu ghép nhóm là:

    S=S2=0,086656≈0,29.

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Giải Toán 12 trang 84 Tập 1

    Giải Toán 12 trang 85 Tập 1

    Giải Toán 12 trang 86 Tập 1

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1 trang 84 Toán 12 Tập 1:Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Hương trong 20 ngày được thống kê lại ở bảng sau...

    Bài 2 trang 84 Toán 12 Tập 1: Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn Chi được thống kê lại ở bảng sau...

    Bài 3 trang 85 Toán 12 Tập 1: Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần tập luyện giải khối rubik 3 × 3,...

    Bài 4 trang 85 Toán 12 Tập 1: Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) bác đã lái xe mỗi ngày trong một tháng ở bảng sau...

    Bài 5 trang 85 Toán 12 Tập 1: Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau...

    Bài 6 trang 86 Toán 12 Tập 1: Thời gian hoàn thành một bài viết chính tả của một số học sinh lớp 4 hai trường X và Y được ghi lại ở bảng sau...

    Bài 7 trang 86 Toán 12 Tập 1: Bảng sau thống kê lại tổng số giờ nắng trong tháng 6 của các năm từ 2002 đến 2021 tại hai trạm quan trắc đặt ở Nha Trang và Quy Nhơn...

    Bài 8 trang 86 Toán 12 Tập 1: Biểu đồ sau mô tả kết quả điều tra về điểm trung bình năm học của học sinh hai trường A và B...

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài tập cuối chương 2 trang 65

    Bài 1: Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm

    Bài 2: Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

    Bài 1: Vẽ đồ thị hàm số bằng phần mềm Geogebra

    Bài 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng máy tính cầm tay

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 172 17/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: