Nội dung bài viết

    Xem thêm

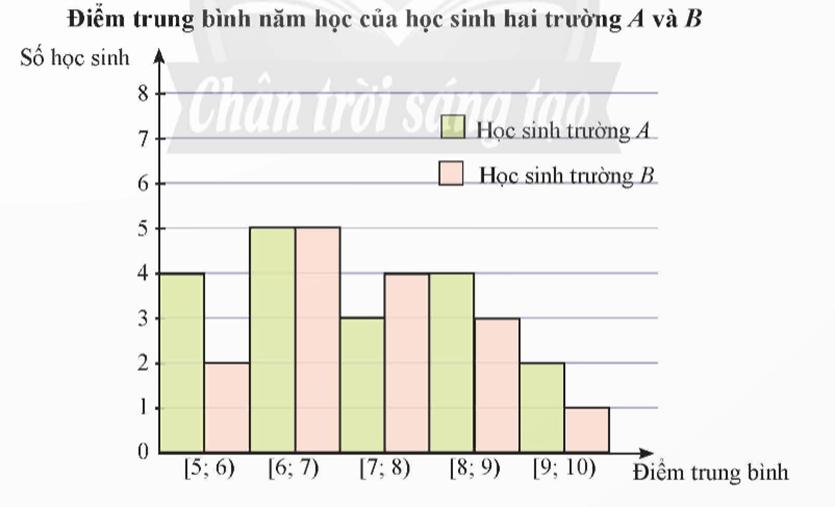
    Biểu đồ sau mô tả kết quả điều tra về điểm trung bình năm học của học sinh hai trường A và B

    Lời giải Bài 8 trang 86 Toán 12 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12.

    1 426 17/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Chân trời sáng tạo Bài tập cuối chương 3 trang 84

    Bài 8 trang 86 Toán 12 Tập 1: Biểu đồ sau mô tả kết quả điều tra về điểm trung bình năm học của học sinh hai trường A và B.

    Bài 8 trang 86 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

    a) Hãy xác định giá trị đại điện cho mỗi nhóm và lập bảng tần số ghép nhóm cho mẫu số liệu trên.

    b) Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn?

    c) Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn?

    Lời giải:

    a) Giá trị đại diện của nhóm [5; 6) là 5,5.

    Giá trị đại diện của nhóm [6; 7) là 6,5.

    Giá trị đại diện của nhóm [7; 8) là 7,5.

    Giá trị đại diện của nhóm [8; 9) là 8,5.

    Giá trị đại diện của nhóm [9; 10) là 9,5.

    Từ biểu đồ, ta có bảng tần số ghép nhóm sau:

    Điểm trung bình

    [5; 6)

    [6; 7)

    [7; 8)

    [8; 9)

    [9; 10)

    Giá trị đại diện

    5,5

    6,5

    7,5

    8,5

    9,5

    Số học sinh trường A

    4

    5

    3

    4

    2

    Số học sinh trường B

    2

    5

    4

    3

    1

    b)

    • Xét mẫu số liệu của trường A:

    Cỡ mẫu nA = 4 + 5 + 3 + 4 + 2 = 18.

    Gọi x1; x2; …; x18 là mẫu số liệu gốc về điểm trung bình năm học của học sinh trường A được xếp theo thứ tự không giảm.

    Ta có x1; …; x4 ∈ [5; 6), x5; …; x9 ∈ [6; 7), x10; x11; x12 ∈ [7; 8),

       x13; …; x16 ∈ [8; 9), x17; x18 ∈ [9; 10).

    Tứ phân vị thứ nhất của mẫu số liệu gốc là x5 ∈ [6; 7).

    Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

    Q1 = 6 +184−45.(7-6) = 6,1.

    Tứ phân vị thứ ba của mẫu số liệu gốc là x14 ∈ [8; 9).

    Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

    Q3 = 8 + 3⋅184−4+5+34.(9-8) = 8,375.

    Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

    ∆Q = Q3 – Q1 = 8,375 – 6,1 = 2,275.

    • Xét mẫu số liệu của trường B:

    Cỡ mẫu nB = 2 + 5 + 4 + 3 + 1 = 15.

    Gọi x1; x2; …; x15 là mẫu số liệu gốc về điểm trung bình năm học của học sinh trường B được xếp theo thứ tự không giảm.

    Ta có x1; x2 ∈ [5; 6), x3; …; x7 ∈ [6; 7), x8; …; x11 ∈ [7; 8),

       x12; x13; x14 ∈ [8; 9), x15 ∈ [9; 10).

    Tứ phân vị thứ nhất của mẫu số liệu gốc là x4 ∈ [6; 7).

    Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

    Q'1=6+154−25⋅7−6=6,35.

    Tứ phân vị thứ ba của mẫu số liệu gốc là x12 ∈ [8; 9).

    Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

    Q'3=8+3⋅154−2+5+43⋅9−8=9712.

    Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

    ∆'Q = Q'3 – Q'1 = 9712 – 6,35 = 2615≈1,73 .

    Vì ∆Q = 2,275 > ∆'Q ≈ 1,73 nên nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường B có điểm trung bình đồng đều hơn.

    c)

    • Xét mẫu số liệu của trường A:

    Số trung bình của mẫu số liệu ghép nhóm là:

    x¯A=4⋅5,5+5⋅6,5+3⋅7,5+4⋅8,5+2⋅9,518=659.

    Phương sai của mẫu số liệu ghép nhóm là:

    SA2=118[4 ∙ (5,5)2 + 5 ∙ (6,5)2 + 3 ∙ (7,5)2 + 4 ∙ (8,5)2 + 2 ∙ (9,5)2] – 6592

    = 569324 .

    Độ lệch chuẩn của mẫu số liệu ghép nhóm là:

    SA=SA2=569324≈1,33.

    • Xét mẫu số liệu của trường B:

    Số trung bình của mẫu số liệu ghép nhóm là:

    x¯B=2⋅5,5+5⋅6,5+4⋅7,5+3⋅8,5+1⋅9,515=21730.

    Phương sai của mẫu số liệu ghép nhóm là:

    SB2=115[2 ∙ (5,5)2 + 5 ∙ (6,5)2 + 4 ∙ (7,5)2 + 3 ∙ (8,5)2 + 1 ∙ (9,5)2] – 217302

    = 284225 .

    Độ lệch chuẩn của mẫu số liệu ghép nhóm là:

    SB=SB2=284225≈1,12.

    Vì SA ≈ 1,33 > SB ≈ 1,12 nên nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh trường B có điểm trung bình đồng đều hơn.

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1 trang 84 Toán 12 Tập 1:Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Hương trong 20 ngày được thống kê lại ở bảng sau...

    Bài 2 trang 84 Toán 12 Tập 1: Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn Chi được thống kê lại ở bảng sau...

    Bài 3 trang 85 Toán 12 Tập 1: Dũng là học sinh rất giỏi chơi rubik, bạn có thể giải nhiều loại khối rubik khác nhau. Trong một lần tập luyện giải khối rubik 3 × 3,...

    Bài 4 trang 85 Toán 12 Tập 1: Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) bác đã lái xe mỗi ngày trong một tháng ở bảng sau...

    Bài 5 trang 85 Toán 12 Tập 1: Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau...

    Bài 6 trang 86 Toán 12 Tập 1: Thời gian hoàn thành một bài viết chính tả của một số học sinh lớp 4 hai trường X và Y được ghi lại ở bảng sau...

    Bài 7 trang 86 Toán 12 Tập 1: Bảng sau thống kê lại tổng số giờ nắng trong tháng 6 của các năm từ 2002 đến 2021 tại hai trạm quan trắc đặt ở Nha Trang và Quy Nhơn...

    Bài 8 trang 86 Toán 12 Tập 1: Biểu đồ sau mô tả kết quả điều tra về điểm trung bình năm học của học sinh hai trường A và B...

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài tập cuối chương 2 trang 65

    Bài 1: Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm

    Bài 2: Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

    Bài 1: Vẽ đồ thị hàm số bằng phần mềm Geogebra

    Bài 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng máy tính cầm tay

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 426 17/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: