Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 60 Tập 1 Cánh diều

    Với giải bài tập Toán lớp 10 trang 60 Tập 1 trong Bài tập cuối chương 3 sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 60 Tập 1.

    1 183 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 60 Tập 1

    Bài 1 trang 60 Toán lớp 10 Tập 1: Tìm tập xác định của mỗi hàm số sau:

    a) y=1x2−x

    b) y=x2−4x+3

    c) y=1x−1

    Lời giải:

    a) Biểu thức 1x2−x xác định khi x2 – x ≠ 0 ⇔ x(x – 1) ≠ 0 ⇔x≠0x≠1.

    Vậy tập xác định của hàm số là D = {x ∈ℝ| x ≠ 0, x ≠ 1} = ℝ\0;  1.

    b) Biểu thức x2−4x+3 xác định khi x2 – 4x + 3 ≥ 0 (1).

    Xét tam thức bậc hai x2 – 4x + 3 có hệ số a = 1 > 0, b = – 4, c = 3 và ∆ = (– 4)2 – 4 . 1 . 3 = 4 > 0.

    Suy ra tam thức có hai nghiệm phân biệt x1 = 1, x2 = 3

    Khi đó ta có bảng xét dấu:

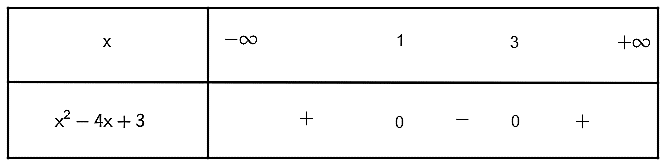
    Giải Toán 10 Bài tập cuối chương 3 - Cánh diều (ảnh 1)

    Suy ra x2 – 4x + 3 ≥ 0 khi và khi chỉ khi x ≤ 1 và x ≥ 3.

    Vậy tập xác định của hàm số đã cho là D = (– ∞; 1] ∪ [3; + ∞).

    c) Biểu thức 1x−1 xác định khi x−1≥0x−1≠0⇔ x – 1 > 0 ⇔ x > 1.

    Vậy tập xác định của hàm số đã cho là D = (1; + ∞).

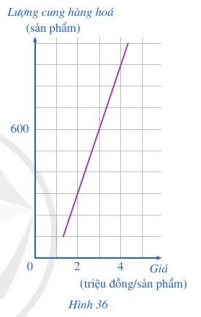
    Bài 2 trang 60 Toán lớp 10 Tập 1: Đồ thị ở Hình 36 cho thấy sự phụ thuộc của lượng hàng hóa được sản xuất (cung) (đơn vị: sản phẩm) bởi giá bán (đơn vị: triệu đồng/sản phẩm) đối với một loại hàng hóa.

    Đồ thị ở Hình 36 cho thấy sự phụ thuộc của lượng hàng hóa được sản xuất

    a) Xác định lượng hàng hóa được sản xuất khi mức giá bán 1 sản phẩm là 2 triệu đồng; 4 triệu đồng.

    b) Biết nhu cầu thị trường đang cần 600 sản phẩm. Hỏi với mức giá bán là bao nhiêu thì thị trường cân bằng (thị trường cân bằng khi sản lượng cung bằng sản lượng cầu)? 

    Lời giải:

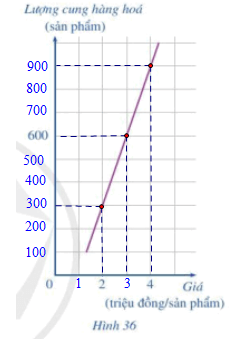
    Hoàn thiện các giá trị trên hai trục ta được đồ thị sau:

    Đồ thị ở Hình 36 cho thấy sự phụ thuộc của lượng hàng hóa được sản xuất

    a) Dựa vào đồ thị trên, ta có:

    Khi mức giá bán 1 sản phẩm là 2 triệu đồng thì lượng hàng hóa được sản xuất tương ứng là 300 sản phẩm.

    Khi mức giá bán 1 sản phẩm là 4 triệu đồng thì lượng hàng hóa được sản xuất tương ứng là 900 sản phẩm.

    b) Để thị trường cân bằng thì sản lượng cung bằng sản lượng cầu mà nhu cầu thị trường đang cần 600 sản phẩm nên mức giá bán là 3 triệu đồng.

    Bài 3 trang 60 Toán lớp 10 Tập 1: Một nhà cung cấp dịch vụ Internet đưa ra hai gói khuyến mại cho người dùng như sau:

    Gói A: Giá cước 190 000 đồng/tháng.

    Nếu trả tiền cước ngay 6 tháng thì sẽ được tặng thêm 1 tháng. 

    Nếu trả tiền cước ngay 12 tháng thì sẽ được tặng thêm 2 tháng. 

    Gói B: Giá cước 189 000 đồng/tháng.

    Nếu trả tiền cước ngay 7 tháng thì số tiền phải trả cho 7 tháng đó là 1 134 000 đồng. 

    Nếu trả tiền cước ngay 15 tháng thì số tiền phải trả cho 15 tháng đó là 2 268 000 đồng. 

    Giả sử số tháng sử dụng Internet là x (x nguyên dương). 

    a) Hãy lập các hàm số thể hiện số tiền phải trả ít nhất theo mỗi gói A, B nếu thời gian dùng không quá 15 tháng. 

    b) Nếu gia đình bạn Minh dùng 15 tháng thì nên chọn gói nào? 

    Lời giải:

    a) Giả sử số tháng sử dụng Internet là x (x nguyên dương, x ≤ 15).

    Gọi y (đồng, y > 0) là số tiền phải trả khi dùng Internet.

    Theo gói A, ta có:

    + Nếu x ≤ 6: y = 190 000.x

    + Nếu 6 < x ≤ 13: y = 190 000 . (x – 1)

    + Nếu 13 < x ≤ 15: y = 190 000 . (x – 2)

    Vậy ta có hàm số thể hiện số tiền ít nhất phải trả theo gói A là:

    y=190  000 .x                  khi  x ≤6190  000 .x−1     khi  6<x≤13190  000.x−2    khi  13<x≤15.

    Theo gói B, ta có:

    + Nếu x < 7: y = 189 000 . x

     + Nếu x = 7: y = 1 134 000

    + Nếu 7 < x < 13: y = 1 134 000 + (x – 7) . 189 000

    + Nếu 13 ≤ x ≤ 15: y = 2 268 000

    Vậy ta có hàm số thể hiện số tiền ít nhất phải trả theo gói B là:

    y=189  000.x        khi  x <71  134  000         khi  x =71  134  000 +x−7.189  000  khi  7 <x <132  268  000       khi  13 ≤x≤15.

    b) Gia đình Minh dùng 15 tháng nên x = 15

    Theo gói A:

     Với x = 15 tháng thì số tiền cước trả ít nhất là:

    190 000.(15 – 2) = 2 470 000 (đồng)

    Do đó với 15 tháng sử dụng Internet theo gói cước A thì gia đình bạn Minh phải trả 2 470 000 đồng.

    Theo gói B:

    Với x = 15 tháng thì số tiền cước phải trả ít nhất là: 2 268 000 (đồng)

    Do đó nếu sử dụng gói cước B thì gia đình bạn Minh phải trả số tiền ít nhất là 2 268 000 đồng.

    Vì 2 268 000 < 2 470 000 nên dùng gói cước B giá thấp hơn.

    Vậy gia đình bạn Minh nếu dùng 15 tháng thì nên chọn gói B để số tiết kiệm chi phí nhất.

    Bài 4 trang 60, 61 Toán lớp 10 Tập 1: Quan sát đồ thị hàm số bậc hai y = ax2 + bx + c ở Hình 37a và Hình 37b rồi nêu:

    a) Dấu của hệ số a;

    b) Tọa độ đỉnh và trục đối xứng;

    c) Khoảng đồng biến;

    d) Khoảng nghịch biến;

    e) Khoảng giá trị x mà y > 0;

    g) Khoảng giá trị x mà y ≤ 0. 

    Quan sát đồ thị hàm số bậc hai y = ax^2 + bx + c ở Hình 37a và Hình 37b

    Lời giải:

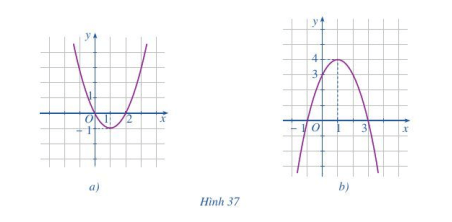
    * Hình 37a: Quan sát đồ thị ta thấy:

    a) Bề lõm của đồ thị hướng lên trên nên hệ số a > 0 hay hệ số a mang dấu “+”.

    b) Tọa độ đỉnh I(1; – 1), trục đối xứng x = 1.

    c) Trên khoảng (1; + ∞) đồ thị hàm số đi lên nên hàm số đồng biến trên khoảng (1; + ∞).

    d) Trên khoảng (– ∞; 1) đồ thị hàm số đi xuống nên hàm số nghịch biến trên khoảng (– ∞; 1).

    e) Trên các khoảng (– ∞; 0) và (2; + ∞) phần Parabol nằm phía trên trục hoành nên hàm số y > 0 với x ∈ (– ∞; 0) ∪ (2; + ∞).

    g) Trên khoảng (0; 2) phần parabol  nằm phía dưới trục hoành nên hàm số y < 0 với x ∈ (0; 2) và f(x) = 0 tại x = 0 hoặc x = 2. Do đó khoảng giá trị của x mà y ≤ 0 là đoạn [0; 2].

    * Hình 37b: Quan sát đồ thị ta thấy,

    a) Bề lõm của đồ thị hướng xuống dưới nên a < 0 hay hệ số a mang dấu “–”.

    b) Tọa độ đỉnh I(1; 4), trục đối xứng x = 1.

    c) Trong khoảng (– ∞; 1) phần parabol đi lên nên hàm số đồng biến trên khoảng (– ∞; 1).

    d) Trong khoảng (1; +∞) phần parabol đi xuống nên hàm số nghịch biến trên khoảng (1; +∞).

    e) Trong khoảng (– 1; 3) phần parabol nằm phía trên trục hoành nên y > 0 khi  x ∈ (– 1; 3).

    g) Trong khoảng (– ∞; – 1) và (3; + ∞) phần parabol nằm phía dưới trục hoành nên để y ≤ 0 khi x ∈ (– ∞; – 1] ∪ [3; + ∞).

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Giải Toán 10 trang 60 Tập 1

    Giải Toán 10 trang 61 Tập 1

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác

    Bài 2: Giải tam giác

    Bài 3: Khái niệm vectơ

    Bài 4: Tổng và hiệu của hai vectơ

    Bài 5: Tích của một số với một vectơ

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 183 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: