Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 100 Tập 1 Cánh diều

    Với giải bài tập Toán lớp 10 trang 100 Tập 1 trong Bài tập cuối chương 4 sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 100 Tập 1.

    1 210 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 100 Tập 1

    Bài 6 trang 100 Toán lớp 10 Tập 1: Để đo khoảng cách giữa hai vị trí M, N ở hai phía ốc đảo, người ta chọn vị trí O bên ngoài ốc đảo sao cho: O không thuộc đường thẳng MN; các khoảng cách OM, ON và góc MON là đo được (Hình 73). Sau khi đo, ta có OM = 200 m, ON = 500 m, MON^=135°.

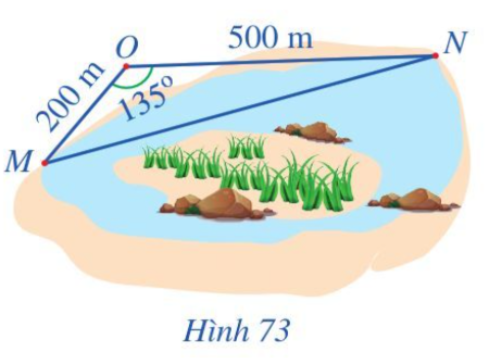
    Khoảng cách giữa hai vị trí M, N là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    Lời giải:

    Ba vị trí O, M, N tạo thành ba đỉnh của tam giác OMN.

    Áp dụng định lí côsin vào tam giác OMN có:

    MN2 = OM2 + ON2 - 2.OM.ON.cos O^

    ⇒ MN2 = 2002 + 5002 - 2.200.500.cos 135o

    ⇒ MN2 ≈ 431 421 m

    ⇒ MN ≈ 657 m.

    Vậy khoảng cách giữa hai điểm M và N khoảng 657 m.

    Bài 7 trang 100 Toán lớp 10 Tập 1: Chứng minh:

    a) Nếu ABCD là hình bình hành thì AB→+AD→+CE→=AE→ với E là điểm bất kì;

    b) Nếu I là trung điểm của đoạn thẳng AB thì MA→+MB→+2IN→=2MN→ với M, N là hai điểm bất kì;

    c) Nếu G là trọng tâm của tam giác ABC thì MA→+MB→+MC→−3MN→=3NG→ với M, N là hai điểm bất kì.

    Lời giải:

    a)

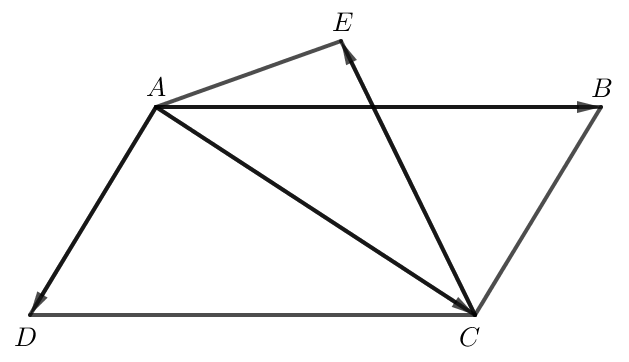
    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    Áp dụng quy tắc hình bình hành ta có AB→+AD→=AC→.

    Do đó AB→+AD→+CE→=AC→+CE→=AE→.

    Vậy AB→+AD→+CE→=AE→.

    b)

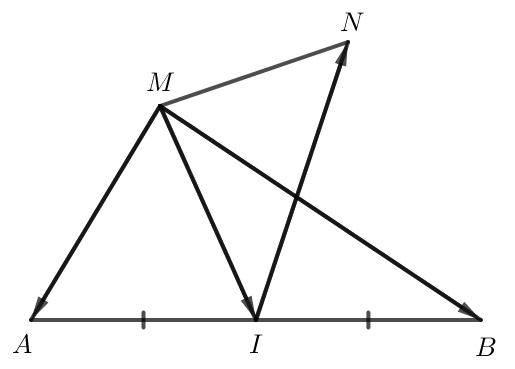
    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    Do I là trung điểm của AB nên MA→+MB→=2MI→.

    Do đó MA→+MB→+2IN→=2MI→+2IN→=2MI→+IN→=2MN→.

    Vậy MA→+MB→+2IN→=2MN→.

    c)

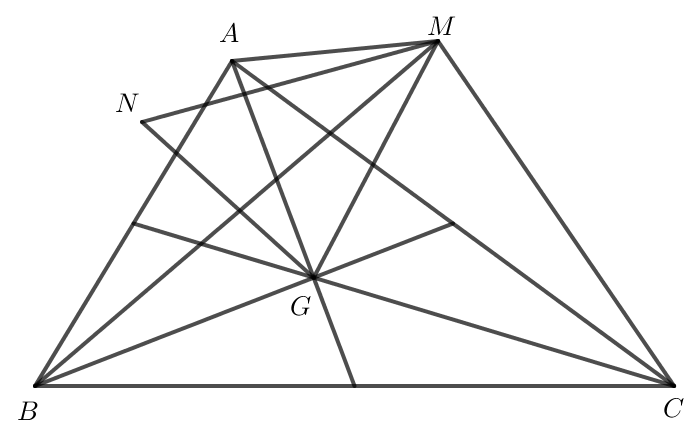
    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    Do G là trọng tâm của tam giác ABC nên MA→+MB→+MC→=3MG→.

    Do đó MA→+MB→+MC→−3MN→=3MG→−3MN→=3MG→−MN→=3NG→.

    Vậy MA→+MB→+MC→−3MN→=3NG→.

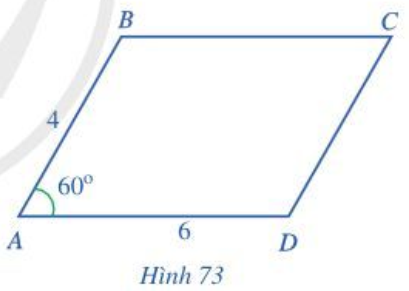
    Bài 8 trang 100 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có AB = 4, AD = 6, BAD^=60° (Hình 74).

    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    a) Biểu thị các vectơ BD→,  AC→ theo AB→,  AD→.

    b) Tính các tích vô hướng AB→ . AD→,  AB→ . AC→,  BD→ . AC→.

    c) Tính độ dài các đường chéo BD, AC.

    Lời giải:

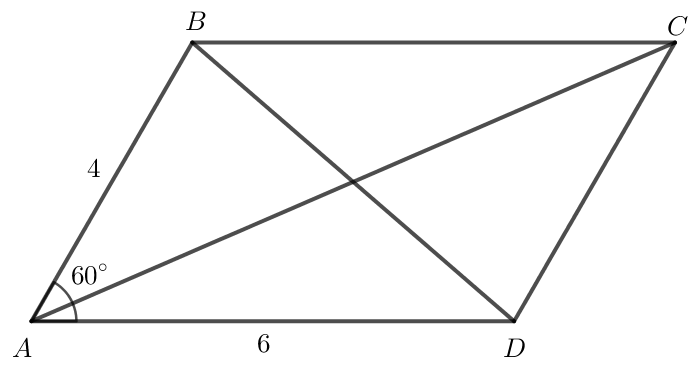
    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    a) Ta có BD→=AD→−AB→.

    Áp dụng quy tắc hình bình hành ta có AB→+AD→=AC→.

    b) Ta có AB→ . AD→=AB→.AD→.cosAB→ , AD→

    = 4 . 6 . cos BAD^ = 24 . cos 60o = 12.

     AB→ . AC→= AB→ . AB→+AD→=AB→2+AB→ . AD→ = 42 + 12  = 28.

    BD→ . AC→=AD→−AB→.AB→+AD→=AD→.AB→+AD→2−AB→2−AB→.AD→ 

    = 62 - 42 = 20.

    c) Áp dụng định lí côsin vào tam giác ABD có:

    BD2 = AB2 + AD2 - 2.AB.AD.cos BAD^

    ⇒ BD2 = 42 + 62 - 2.4.6.cos 60o

    ⇒ BD2 = 28

    ⇒ BD = 27

    Do ABCD là hình bình hành nên BAD^+ADC^=180°.

    Do đó ADC^=180°−BAD^=180°−60°=120°.

    Áp dụng định lí côsin vào tam giác ADC có:

    CD2 = AD2 + DC2 - 2.AD.DC.cos ADC^

    ⇒ CD2 = 62 + 42 - 2.6.4.cos 120o

    ⇒ CD2 = 76

    ⇒ CD = 219

    Vậy BD = 27; CD = 219.

    Bài 9 trang 100 Toán lớp 10 Tập 1: Hai lực F1→,  F2→ cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc F1→,  F2→=α làm cho vật di chuyển theo hướng từ O đến C (Hình 75). Lập công thức tính cường độ của hợp lực F→ làm cho vật di chuyển theo hướng từ O đến C (giả sử chỉ có đúng hai lực F1→,  F2→ làm cho vật di chuyển).

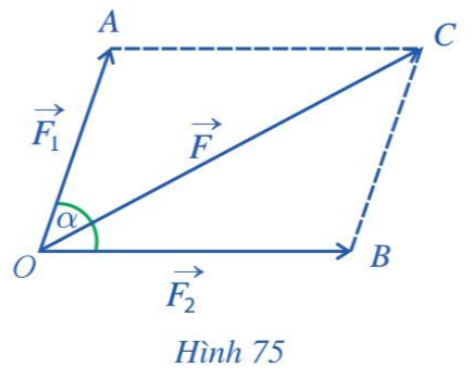
    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    Lời giải:

    Do AOBC là hình bình hành nên AOB^+OBC^=180°.

    Do đó OBC^=180°−α.

    Ta có F1→.F2→=F1→.F2→.cosF1→,F2→=F1→.F2→.cosα.

    Áp dụng định lí côsin vào tam giác OBC có:

    OC2 = OB2 + BC2 - 2.OB.OC.cos OBC^

    ⇒F→2=F2→2+F1→2−2.F2→.F1→.cos180°−α

    ⇒F→2=F2→2+F1→2−2.F2→.F1→.cosα.cos180°−α

    ⇒F→=F2→2+F1→2−2.F2→.F1→.cosα.cos180°−α.

    Vậy công thức tính cường độ của hợp lực F→ là ⇒F→=F2→2+F1→2−2.F2→.F1→.cosα.cos180°−α

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Giải Toán 10 trang 99 Tập 1

    Giải Toán 10 trang 100 Tập 1

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Chủ đề 1: Đo góc

    Bài 1: Mệnh đề toán học

    Bài 2: Tập hợp. Các phép toán trên tập hợp

    Bài tập cuối chương 1

    Bài 1: Bất phương trình bậc nhất hai ẩn

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 210 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: