Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 99 Tập 1 Cánh diều

    Với giải bài tập Toán lớp 10 trang 99 Tập 1 trong Bài tập cuối chương 4 sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 99 Tập 1.

    1 208 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 99 Tập 1

    Bài 1 trang 99 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 3, AC = 4, BAC^=120°.  Tính (làm tròn kết quả đến hàng đơn vị):

    a) Độ dài cạnh BC và độ lớn góc B;

    b) Bán kính đường tròn ngoại tiếp;

    c) Diện tích của tam giác;

    d) Độ dài đường cao xuất phát từ A;

    e) AB→ . AC→, AM→ .BC→ với M là trung điểm của BC.

    Lời giải:

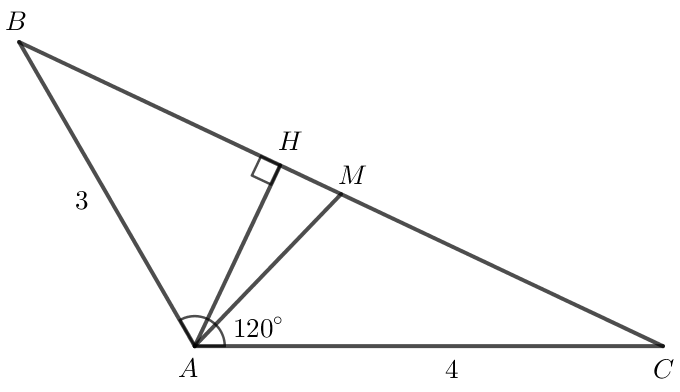
    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    a) Áp dụng định lí côsin vào tam giác ABC có:

    BC2 = AB2 + AC2 - 2.AB.AC.cos A^

    ⇒ BC2 = 32 + 42 - 2.3.4. cos 120o

    ⇒ BC2 = 37

    ⇒ BC ≈ 6

    Áp dụng định lí sin vào tam giác ABC có:

    BCsinA=ACsinB

    ⇒sinB=AC.sinABC=4.sin120°6=13

    ⇒ B^ ≈ 35o

    b) Áp dụng định lí sin vào tam giác ABC có:

    BCsinA=2R

    ⇒ 2R = 43

    ⇒ R ≈ 3.

    c) Nửa chu vi của tam giác ABC là: 3+4+62 = 6,5.

    Diện tích của tam giác ABC là:

    6,5.6,5−3.6,5−4.6,5−6 ≈ 5. (đvdt)

    Vậy diện tích tam giác ABC là 5 (đvdt).

    d) Gọi H là chân đường cao kẻ từ A đến BC.

    Khi đó diện tích tam giác ABC là: SABC = 12AH.BC = 12AH.6 = 3AH.

    Mà theo ý c) ta có diện tích tam giác ABC là 5

    ⇒ 3AH = 5

    ⇒ AH = 53 ≈ 2.

    Vậy độ dài đường cao kẻ từ A là 2.

    d) Ta có AB→.AC→=AB→.AC→.cosAB→,AC→

    = 3 . 4 . cos 120o = -6.

    Do M là trung điểm của BC nên AM→=12AB→+12AC→.

    Khi đó AM→.BC→=12AB→+12AC→.BC→

    =12AB→+12AC→.AC→−AB→

    =12AB→.AC→−12AB→2+12AC→2−12AC→.AB→

    =12AC→2−12AB→2

    =12.42−12.32

    =12.42−12.32

    =72≈4

    Vậy AB→.AC→=-6. AM→. BC→≈4

    Bài 2 trang 99 Toán lớp 10 Tập 1: Không dùng máy tính cầm tay, hãy tính giá trị của các biểu thức sau:

    A = (sin 20° + sin 70°)2 + (cos 20° + cos 110°)2,

    B = tan 20° + cot 20° + tan 110° + cot 110°.

    Lời giải:

    a) A = (sin 20° + sin 70°)2 + (cos 20° + cos 110°)2

    A = [sin(90o - 70o) + sin 70o]2 + [cos(90o - 70o) + cos(180o - 70o)]

    A = (cos 70o + sin 70o)2 + (sin 70o - cos 70o)2

    A = cos2 70o + 2.cos 70o.sin 70o + sin2 70o + sin2 70o - 2.cos 70o.sin 70o + cos2 70o

    A = 2(cos2 70o + sin2 70o)

    A = 2.1

    A = 2

    Vậy A = 2.

    b) B = tan 20° + cot 20° + tan 110° + cot 110°

    = tan(90° – 70°) + cot(90° – 70°) + tan(180° – 70°) + cot(180° – 70°)

    = cot 70° + tan 70° + (– tan 70°) + (– cot 70°)

    = (cot 70° – cot 70°) + (tan 70° – tan 70°)

    = 0

    Vậy B = 0.

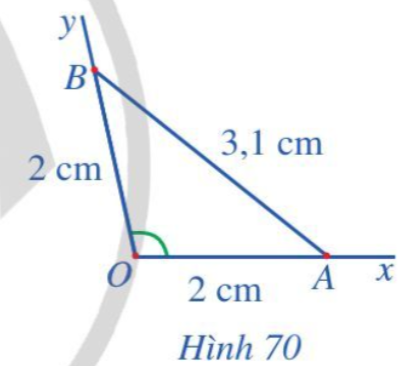
    Bài 3 trang 99 Toán lớp 10 Tập 1: Không dùng thước đo góc, làm thế nào để biết số đo góc đó.

    Bạn Hoài vẽ góc xOy và đố bạn Đông làm thế nào để có thể biết được số đo góc của góc này khi không có thước đo góc. Bạn Đông làm như sau (Hình 70):

    - Chọn các điểm A, B lần lượt thuộc các tia Ox và Oy sao cho OA = OB = 2 cm;

    - Đo độ dài đoạn thẳng AB được AB = 3,1 cm.

    Từ các dữ kiện trên bạn Đông tính được cosxOy^, từ đó suy ra độ lớn góc xOy.

    Em hãy cho biết số đo góc xOy mà bạn Đông tính được bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị).

    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    Lời giải:

    Áp dụng định lí côsin vào tam giác OAB có:

    AB2 = OA2 + OB2 - 2.OA.OB.cos O^

    ⇒cosO^=OA2+OB2−AB22.OA.OB

    ⇒cosO^=22+22−3,122.2.2

    ⇒cosO^=−161800

    ⇒O^ ≈ 102o.

    Vậy bạn Đông tính được xOy^ bằng 102o.

    Bài 4 trang 99 Toán lớp 10 Tập 1: Có hai trạm quan sát A và B ven hồ và một trạm quan sát C ở giữa hồ. Để tính khoảng cách từ A và từ B đến C, người ta làm như sau (Hình 71):

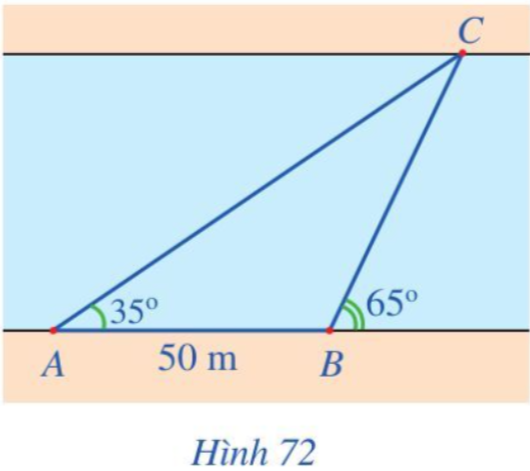
    - Đo góc BAC được 60°, đo góc ABC được 45°;

    - Đo khoảng cách AB được 1 200 m.

    Khoảng cách từ trạm C đến các trạm A và B bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    Lời giải:

    Ba vị trí A, B, C tạo thành ba đỉnh của tam giác ABC.

    Trong tam giác ABC có C^=180°−A^−B^=180°−60°−45°=75°.

    Áp dụng định lí sin vào tam giác ABC có:

    ABsinC=BCsinA=CAsinB

    Do đó BC=AB.sinAsinC=1200.sin60°sin75° ≈ 1 076 m;

    CA=AB.sinBsinC=1200.sin45°sin75° ≈ 878 m.

    Vậy khoảng cách từ trạm C đến trạm A và trạm B lần lượt khoảng 878 m và 1 076 m.

    Bài 5 trang 99 Toán lớp 10 Tập 1: Một người đứng ở bờ sông, muốn đo độ rộng của khúc sông chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ song song với nhau).

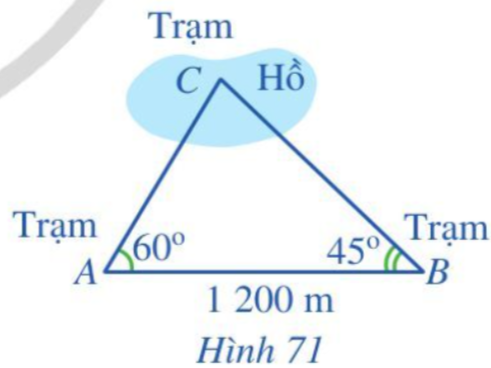
    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    Từ vị trí đang đứng A, người đó đo được góc nghiêng α = 35° so với bờ sông tới một vị trí C quan sát được ở phía bờ bên kia. Sau đó di chuyển dọc bờ sông đến vị trí B cách A một khoảng d = 50 m và tiếp tục đo được góc nghiêng β = 65° so với bờ bên kia tới vị trí C đã chọn (Hình 72). Hỏi độ rộng của khúc sông chảy qua vị trí người đó đang đứng là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

    Lời giải:

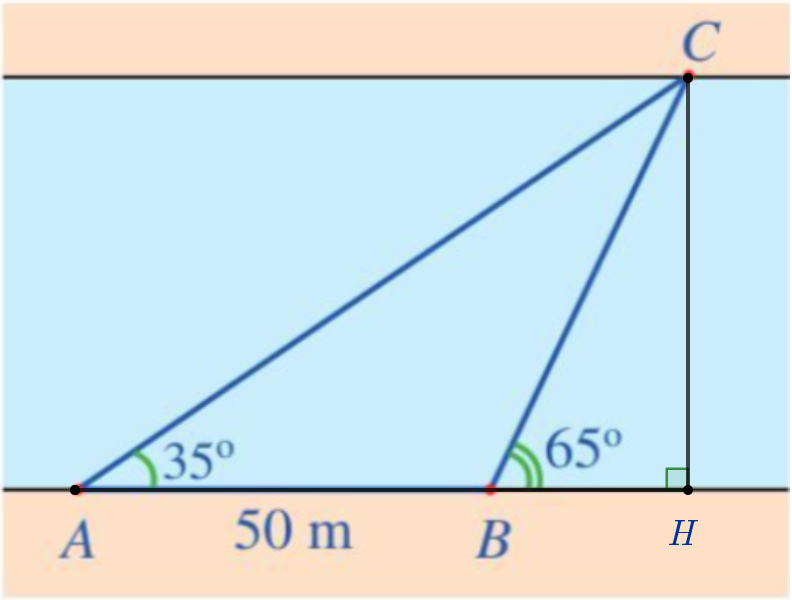
    Giải Toán 10 Bài tập cuối chương 4 - Cánh diều (ảnh 1)

    Gọi H là chân đường cao kẻ từ C đến AB.

    Khi đó độ rộng của khúc sông là CH.

    Ta có CBH^ là góc ngoài tại đỉnh B của tam giác ABC nên CBH^=BAC^+BCA^.

    Do đó BCA^=CBH^−BAC^=65°−35°=30°.

    Áp dụng định lí sin vào tam giác ABC có:

    ABsinC=BCsinA

    ⇒BC=AB.sinAsinC=50.sin35°sin30° ≈ 57,4 m.

    Tam giác CBH vuông tại B nên:

    sinCBH^=CHCB

    ⇒ CH = CB . sin CBH^ = 57,4 . sin 65o

    ⇒ CH ≈ 52 m

    Vậy độ rộng của khúc sông khoảng 52 m.

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Giải Toán 10 trang 99 Tập 1

    Giải Toán 10 trang 100 Tập 1

    Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: 

    Chủ đề 1: Đo góc

    Bài 1: Mệnh đề toán học

    Bài 2: Tập hợp. Các phép toán trên tập hợp

    Bài tập cuối chương 1

    Bài 1: Bất phương trình bậc nhất hai ẩn

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 208 16/02/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: