Giải SBT Toán 6 Bài 3 (Chân trời sáng tạo): So sánh phân số

Mục lục Giải SBT Toán 6 Bài 3: So sánh phân số

Bài 1 trang 16 SBT Toán 6: So sánh hai phân số:

a) $\frac{-15}{1001}$ và $\frac{-12}{1001}$;

b) $\frac{34}{-77}$ và $\frac{43}{-77}$;

c) $\frac{77}{-36}$ và $\frac{-97}{45}$.

Lời giải:

Để so sánh hai phân số bằng cách đưa về cùng mẫu số thì ta thực hiện theo hai bước sau:

Bước 1: Viết hai phân số về dạng hai phân số có cùng một mẫu số dương.

Bước 2: So sánh tử số, phân số nào có tử nhỏ hơn thì phân số đó nhỏ hơn, phân số nào có tử lớn hơn thì phân số đó lớn hơn.

a) Hai phân số $\frac{-15}{1001}$ và $\frac{-12}{1001}$ có cùng một mẫu số dương nên ta so sánh tử số của hai phân số đó.

Vì −15 < −12 nên $\frac{-15}{1001}<\frac{-12}{1001}$.

Vậy $\frac{-15}{1001}<\frac{-12}{1001}$.

b) Đưa hai phân số về cùng một mẫu số dương: $\frac{34}{-77}=\frac{-34}{77}$ và $\frac{43}{-77}=\frac{-43}{77}$.

Vì −34 > −43 nên $\frac{-34}{77}>\frac{-43}{77}$.

Vậy $\frac{34}{-77}>\frac{43}{-77}$.

c) Đưa hai phân số về cùng một mẫu số dương bằng cách quy đồng mẫu số hai phân số:

Mẫu số chung: 180.

Ta thực hiện:

$\frac{77}{-36}=\frac{77.(-5)}{-36.(-5)}=\frac{-385}{180}$

và $\frac{-97}{45}=\frac{-97.4}{45.4}=\frac{-388}{180}$.

Vì −385 > −388 nên $\frac{-385}{180}>\frac{-388}{180}$ hay $\frac{77}{-36}>\frac{-97}{45}.$

Vậy $\frac{77}{-36}>\frac{-97}{45}.$

Bài 2 trang 16 SBT Toán 6: So sánh:

a) $\frac{501}{-101}$ và −5;

b) −12 và $\frac{-145}{12}$.

Lời giải:

Để so sánh một số nguyên và một phân số, ta có thể làm theo hai cách sau:

Cách 1: Đưa số nguyên về dạng phân số có cùng mẫu dương với phân số và phân số có mẫu số dương, rồi so sánh tử số của hai phân số.

Cách 2: Đưa số nguyên về dạng phân số có mẫu số là 1, tử số là số nguyên đó, sau đó tiến hành quy đồng mẫu số hai phân số (đưa hai phân số về cùng một mẫu số dương).

a) Cách 1: Ta có: $\frac{501}{-101}=\frac{-501}{101}$ và −5 $=\frac{-505}{101}$.

Vì −501 > −505 nên $\frac{-501}{101}>\frac{-505}{101}$.

Vậy $\frac{501}{-101}>-5$.

Cách 2: Ta có: $-5=\frac{-5}{1}$.

Quy đồng mẫu số hai phân số $\frac{501}{-101}$ và $\frac{-5}{1}$, ta được:

$\frac{501}{-101}=\frac{-501}{101}$ và $\frac{-5}{1}=\frac{-5.101}{1.101}=\frac{-505}{101}$.

Vì −501 > −505 nên $\frac{-501}{101}>\frac{-505}{101}$.

Vậy $\frac{501}{-101}>-5$.

b) −12 và $\frac{-145}{12}$

Cách 1: Ta có: −12 $=\frac{-144}{12}$.

Vì −144 > −145 nên $\frac{-144}{12}>\frac{-145}{12}$ hay $-12>\frac{-145}{12}$.

Vậy $-12>\frac{-145}{12}$.

Cách 2: Ta có: $-5=\frac{-5}{1}$.

Quy đồng mẫu số hai phân số $\frac{501}{-101}$ và $\frac{-5}{1}$, ta được:

$\frac{501}{-101}=\frac{-501}{101}$ và $\frac{-5}{1}=\frac{-5.101}{1.101}=\frac{-505}{101}$.

Vì −501 > −505 nên $\frac{-501}{101}>\frac{-505}{101}$ hay $\frac{501}{-101}>-5$

Vậy $\frac{501}{-101}>-5$.

Bài 3 trang 16 SBT Toán 6: Sắp xếp các số theo thứ tự

a) tăng dần: $-4;\frac{10}{3};\frac{9}{-2}$ và $\frac{-22}{-7}$.

b) giảm dần: $\frac{25}{-6};\frac{-47}{-12};4$ và $\frac{-31}{8}$.

Lời giải:

Để sắp xếp các phân số theo thứ tự tăng dần hoặc giảm dần, ta làm như sau:

Bước 1: Đưa các phân số vào hai nhóm: nhóm các phân số dương và nhóm các phân số âm.

+ Phân số dương là phân số có tử số và mẫu số là các số nguyên cùng dấu.

+ Phân số âm là phân số có tử số và mẫu số là các số nguyên trái dấu.

Bước 2: So sánh các phân số dương với nhau, các phân số âm với nhau (bằng cách đưa về cùng mẫu số dương rồi so sánh tử số).

Bước 3: Sắp xếp các phân số trên theo thứ tự từ tăng dần hoặc giảm dần (phân số âm luôn bé hơn phân số dương).

a) Ta có $-4=\frac{-4}{1}$.

+ Các phân số dương: $\frac{10}{3};\frac{-22}{-7}.$

+ Các phân số âm: $\frac{-4}{1};\frac{9}{-2}$.

Ta so sánh các phân số dương với nhau, các phân số âm với nhau:

+ So sánh $\frac{10}{3}$ và $\frac{-22}{-7}$

Mẫu số chung: 21.

Ta thực hiện:

$\frac{10}{3}=\frac{10.7}{3.7}=\frac{70}{21}$;

$\frac{-22}{-7}=\frac{(-22).(-3)}{(-7).(-3)}=\frac{66}{21}$.

Vì 70 > 66 nên $\frac{70}{21}>\frac{66}{21}$ hay $\frac{10}{3}>\frac{-22}{-7}.$

+ So sánh $\frac{-4}{1}$ và $\frac{9}{-2}$

Mẫu số chung: 2.

Ta thực hiện:

$\frac{-4}{1}=\frac{-4.2}{1.2}=\frac{-8}{2}$;

$\frac{9}{-2}=\frac{-9}{2}$.

Vì −8 > −9 nên $\frac{-8}{2}>\frac{-9}{2}$ hay $\frac{-4}{1}>\frac{-9}{2}$

Từ đó, suy ra $\frac{-9}{2}<\frac{-4}{1}<\frac{-22}{-7}<\frac{10}{3}.$

Vậy ta sắp xếp được theo thứ tự tăng dần như sau: $\frac{-9}{2};-4;\frac{-22}{-7};\frac{10}{3}.$

b) Ta có $4=\frac{4}{1}$.

+ Các phân số dương: $\frac{4}{1};\frac{-47}{-12}.$

+ Các phân số âm: $\frac{25}{-6};\frac{-31}{8}.$

Ta so sánh các phân số dương với nhau, các phân số âm với nhau:

+ So sánh $\frac{4}{1}$ và $\frac{-47}{-12}.$

Mẫu số chung: 12.

Ta thực hiện:

$\frac{4}{1}=\frac{4.12}{1.12}=\frac{48}{12}$ ;

$\frac{-47}{-12}=\frac{47}{12}$.

Vì 48 > 47 nên $\frac{48}{12}>\frac{47}{12}$ hay $\frac{4}{1}>\frac{-47}{-12}.$

+ So sánh $\frac{25}{-6}$ và $\frac{-31}{8}.$

Mẫu số chung: 24.

Ta thực hiện:

$\frac{25}{-6}=\frac{25.(-4)}{(-6).(-4)}=\frac{-100}{24}$ ;

$\frac{-31}{8}=\frac{-31.3}{8.3}=\frac{-93}{24}$.

Vì −100 < −93 nên $\frac{-100}{24}<\frac{-93}{24}$ hay $\frac{25}{-6}<\frac{-31}{8}$.

Từ đó, suy ra $\frac{4}{1}>\frac{-47}{-12}>\frac{-31}{8}>\frac{25}{-6}.$

Vậy ta sắp xếp được theo thứ tự giảm dần như sau: $4;\frac{-47}{-12};\frac{-31}{8};\frac{25}{-6}.$

Bài 4 trang 16 SBT Toán 6: Khẳng định sau đúng hay sai? Vì sao?

a) $\frac{-8}{15}<\frac{1}{-2};$

b) $\frac{-4}{3}>\frac{5}{-4}$.

Lời giải:

Đưa hai phân số về cùng mẫu dương rồi so sánh tử số, sau đó kiểm tra khẳng định đó đúng hay sai.

a) Mẫu số chung: 30.

Ta thực hiện:

$$\begin{gathered} \frac{-8}{15}=\frac{-8.2}{15.2}=\frac{-16}{30}; \\ \frac{1}{-2}=\frac{1.(-15)}{(-2)(-15)}=\frac{-15}{30} \end{gathered}$$

Vì −16 < −15 nên $\frac{-16}{30}<\frac{-15}{30}$ hay $\frac{-8}{15}<\frac{1}{-2}.$

Vậy khẳng định $\frac{-8}{15}<\frac{1}{-2}$ đúng.

b) Mẫu số chung: 12.

Ta thực hiện:

$$\begin{gathered} \frac{-4}{3}=\frac{-4.4}{3.4}=\frac{-16}{12}; \\ \frac{5}{-4}=\frac{5.(-3)}{(-4).(-3)}=\frac{-15}{12}. \end{gathered}$$

Vì −16 < −15 nên $\frac{-16}{12}<\frac{-15}{12}$ hay $\frac{-4}{3}<\frac{5}{-4}$.

Vậy khẳng định $\frac{-4}{3}>\frac{5}{-4}$ sai.

Bài 5 trang 16 SBT Toán 6: Tìm số nguyên x thỏa mãn:

a) $\frac{-3}{7}<\frac{x}{7}<\frac{2}{7};$

b) $\frac{4}{-3}<\frac{x}{-3}<\frac{1}{-3}$.

Lời giải:

Đưa các phân số về cùng mẫu dương để so sánh tử số, sau đó tìm các số nguyên x thỏa mãn.

a) Ba phân số $\frac{-3}{7};\frac{x}{7};\frac{2}{7}$ có cùng mẫu dương nên:
Để $\frac{-3}{7}<\frac{x}{7}<\frac{2}{7}$ thì −3 < x < 2.

Các số nguyên x thoả mãn lớn hơn −3 nhỏ hơn 2 là: −2; −1; 0; 1.

Vậy số nguyên x thỏa mãn $\frac{-3}{7}<\frac{x}{7}<\frac{2}{7}$ là −2; −1; 0; 1.

b) $\frac{4}{-3}<\frac{x}{-3}<\frac{1}{3}$

Ta có:

$\frac{4}{-3}=\frac{-4}{3};\frac{x}{-3}=\frac{-x}{3}$

Viết lại như sau:

$\frac{-4}{3}<\frac{-x}{3}<\frac{1}{3}$.

Phân số $\frac{-x}{3}$ có cùng mẫu số dương với hai phân số $\frac{4}{-3};\frac{1}{3}$.

Do đó để $\frac{-4}{3}<\frac{-\mathrm{x}}{3}<\frac{1}{3}$ thì −4 < −x < 1 suy ra 4 > x > −1.

Các số nguyên x thỏa mãn – 1 < x < 4 là: 0; 1; 2; 3.

Vậy số nguyên x thỏa mãn $\frac{4}{-3}<\frac{\mathrm{x}}{-3}<\frac{1}{3}$ là 0; 1; 2; 3.

Bài 6 trang 16 SBT Toán 6: Một lớp học có nhiều học sinh yêu thích thể thao. Trong ngày hội thể thao của trường, lớp đã có $\frac{1}{2}$ số học sinh đăng kí thi đấu bóng đá, $\frac{2}{5}$ số học sinh đăng kí thi đấu bóng chuyền, $\frac{11}{20}$ số học sinh đăng kí thi đấu kéo co và $\frac{3}{10}$ số học sinh đăng kí thi đấu cầu lông. Hãy cho biết môn thi đấu nào được học sinh đăng kí nhiều nhất và môn thi đấu nào được học sinh đăng kí ít nhất (một học sinh có thể thi đấu nhiều môn).

Lời giải:

Bài toán đưa về sắp xếp các phân số $\frac{1}{2};\frac{2}{5};\frac{11}{20};\frac{3}{10}$ theo thứ tự tăng dần hoặc giảm dần. Sau đó tìm môn thi đấu được học sinh đăng kí nhiều nhất và ít nhất.

Quy đồng mẫu số các phân số $\frac{1}{2};\frac{2}{5};\frac{11}{20};\frac{3}{10}$ , ta được:

$$\begin{gathered} \frac{1}{2}=\frac{1.10}{2.10}=\frac{10}{20}; \\ \frac{2}{5}=\frac{2.4}{5.4}=\frac{8}{20}; \\ \frac{3}{10}=\frac{3.2}{10.2}=\frac{6}{20}\text{\hspace{0.17em};} \end{gathered}$$

giữ nguyên phân số $\frac{11}{20}$.

Vì 6 < 8 < 10 < 11 nên $\frac{6}{20}<\frac{8}{20}<\frac{10}{20}<\frac{11}{20}$ hay $\frac{3}{10}<\frac{2}{5}<\frac{1}{2}<\frac{11}{20}$.

Vậy môn thể thao được kí nhiều nhất tương ứng với $\frac{11}{20}$ số học sinh đăng kí thi đấu là kéo co; môn thể thao được kí ít nhất tương ứng với $\frac{3}{10}$ số học sinh đăng kí thi đấu là cầu lông.

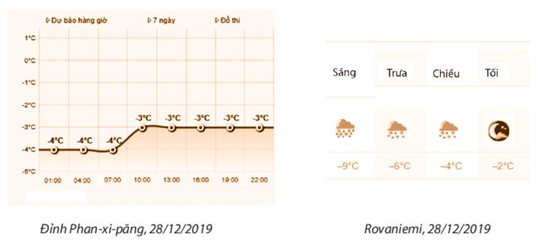
Bài 7 trang 16, 17 SBT Toán 6: Quan sát thông tin trong cùng thời gian về nhiệt độ ở đỉnh Phan-xi-păng (Lào Cai, Việt Nam) và nhiệt độ ở Rovaniemi (Lapland, Phần Lan) trong hình sau và cho biết:

a) Số đo nhiệt độ trung bình trong ngày 28/12/2019 ở đỉnh Phan-xi-păng và ở Rovaniemi là hai phân số nào?

b) So sánh hai phân số ở câu a) và cho biết ý nghĩa thực tiễn của kết quả so sánh.

Lời giải:

a) Từ thông tin có trong hình, ta thấy nhiệt độ trung bình trong ngày 28/12/2019 ở đỉnh Phan-xi-păng là trung bình cộng của nhiệt độ tại 8 thời điểm, còn nhiệt độ trung bình tại Rovaniemi là trung bình cộng tại 4 thời điểm.

Trung bình cộng của nhiệt độ tại 8 thời điểm ở Phan-xi-păng là:

[(−4) + (−4) + (−4) + (−3) +(−3) + (−3) + (−3) + (−3)] : 8

= [(−4) . 3 + (−3) . 5] : 8 = $\frac{-27}{8}$ (^oC).

Trung bình cộng nhiệt độ tại 4 thời điểm ở Rovaniemi là:

[(−9) + (−6) + (−4) + (−2)] : 4 = $\frac{-21}{4}$ (^oC).

Vậy phân số biểu thị nhiệt độ trung bình ở đỉnh Phan-xi-păng và Rovaniemi lần lượt là $\frac{-27}{8}$ và $\frac{-21}{4}$.

b) Ta có $\frac{-21}{4}=\frac{-21.2}{4.2}=\frac{-42}{8}$ .

Vì -42 < -27 nên $\frac{-42}{8}<\frac{-27}{8}$nên nhiệt độ trung bình ngày 28/12/2019 tại Rovaniemi thấp hơn ở đỉnh Phan-xi-păng.

Ý nghĩa thực tiễn: Ngày 28/12/2019, ở Rovaniemi lạnh hơn ở đỉnh Phan-xi-păng.

Bài 8 trang 17 SBT Toán 6:

a) Số nguyên n có điều kiện gì thì phân số $\frac{\mathrm{n}}{-5}$ là phân số dương?

b) Số nguyên m có điều kiện gì thì phân số $\frac{-2}{-\mathrm{m}}$ là phân số âm?

Lời giải:

Phân số dương là phân số lớn hơn 0 (hay phân số có tử số và mẫu số cùng dấu).

Phân số âm là phân số nhỏ hơn 0 (hay phân số có tử số và mẫu số trái dấu).

a) Cách 1:

Ta có: $\frac{\mathrm{n}}{-5}=\frac{-\mathrm{n}}{5}$ và $0=\frac{0}{5}$;

Để $\frac{\mathrm{n}}{-5}$ là phân số dương thì $\frac{\mathrm{n}}{-5}>0$ hay $\frac{-\mathrm{n}}{5}>\frac{0}{5}$.

Khi đó −n > 0 suy ra n < 0.

Vậy n là số nguyên âm thì phân số $\frac{\mathrm{n}}{-5}$ là phân số dương.

Cách 2: Để phân số $\frac{\mathrm{n}}{-5}$ là phân số dương thì n và −5 là hai số nguyên cùng dấu.

Mà số −5 mang dấu trừ (−) nên n mang trừ (−).

Vậy n là số nguyên âm thì phân số $\frac{\mathrm{n}}{-5}$ là phân số dương.

b) Cách 1: Ta có: $\frac{-2}{-\mathrm{m}}=\frac{2}{\mathrm{m}}$

Để $\frac{-2}{-\mathrm{m}}$ là phân số âm thì $\frac{-2}{-\mathrm{m}}<0$ hay $\frac{2}{\mathrm{m}}<0$

Vì 2 > 0 nên $\frac{2}{\mathrm{m}}<0$ khi m < 0.

Vậy m là số nguyên âm thì phân số $\frac{-2}{-\mathrm{m}}$ là phân số âm.

Cách 2: Để phân số $\frac{-2}{-\mathrm{m}}$ là phân số âm thì −2 và −m là hai số nguyên trái dấu.

Mà số −2 mang dấu trừ (−) nên −m mang cộng (+) hay m mang dấu trừ (−).

Vậy m là số nguyên âm thì phân số $\frac{-2}{-\mathrm{m}}$ là phân số âm.

Xem thêm lời giải sách bài tập Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Phép cộng và phép trừ phân số

Bài 5: Phép nhân và phép chia phân số

Bài 6: Giá trị của một phân số

Bài 7: Hỗn số

Bài tập cuối chương 5