Nội dung bài viết

    Xem thêm

    Giải SBT Toán 6 Bài 6 (Chân trời sáng tạo): Chia hết và chia có dư. Tính chất chia hết của một tổng

    Lời giải sách bài tập Toán lớp 6 Bài 6: Chia hết và chia có dư. Tính chất chia hết của một tổng sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong sách bài tập Toán 6.

    1 1,226 15/03/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Mục lục Giải SBT Toán 6 Bài 6: Chia hết và chia có dư. Tính chất chia hết của một tổng

    Bài 1 trang 19 SBT Toán 6 Tập 1: Chọn câu sai:

    a) 11.44 + 16 chia hết cho 4 nên chia hết cho 2;

    b) 24.8 – 17 chia hết cho 3;

    c) 136.3 – 2.34 chia hết cho 9;

    d) Tích của ba số tự nhiên liên tiếp chia hết cho 2, cho 3.

    Lời giải

    a) Phát biểu a) là đúng vì 11.44 + 16 chia hết cho 4 mà 4 lại chia hết cho 2 nên 11.44 + 16 chia hết cho 2.

    b) Vì 24 chia hết cho 3 nên 24.8 chia hết cho 3

    Mà 17 không chia hết cho 3

    Nên theo tính chất chia hết của một hiệu thì 24.8 – 17 không chia hết cho 3.

    Do đó phát biểu b) sai.

    c) Ta có: 2.34 = 2.32.32 = 2.9.9 chia hết cho 9;

    Mà 136.3 không chia hết cho 9

    Nên theo tính chất chia hết của một hiệu thì 136.3 – 2.34 không chia hết cho 9.

    Do đó phát biểu c) là sai.

    d) Gọi ba số tự nhiên liên tiếp là n, n + 1, n + 2 với n là số tự nhiên.

    +) Quan hệ chia hết của n(n + 1)(n + 2) với 2

    - Nếu n là số chẵn thì n chia hết cho 2. Suy ra n(n + 1)(n + 2) chia hết cho 2.

    - Nếu n là số lẻ thì n + 1 là số chẵn nên n + 1 chia hết cho 2. Suy ra n(n + 1)(n + 2) chia hết cho 2.

    Do đó n(n + 1)(n + 2) chia hết cho 2 với mọi số tự nhiên n (1).

    +) Quan hệ chia hết của n(n + 1)(n + 2) với 3

    - Nếu n chia hết cho 3 thì n(n + 1)(n + 2) chia hết cho 3.

    - Nếu n chia cho 3 dư 1 thì n = 3k + 1 với k là số tự nhiên. Khi đó n + 2 = 3k + 3 = 3(k + 1) chia hết cho 3. Suy ra n(n + 1)(n + 2) chia hết cho 3.

    - Nếu n chia cho 3 dư 2 thì n = 3k + 2 với k là số tự nhiên. Khi đó n + 1 = 3k + 3 = 3(k + 1) chia hết cho 3. Suy ra n(n + 1)(n + 2) chia hết cho 3.

    Do đó n(n + 1)(n + 2) chia hết cho 3 với mọi số tự nhiên n (2).

    Từ (1) và (2) suy ra n(n + 1)(n + 2) chia hết cho 2 và 3 với mọi số tự nhiên n hay tích của ba số tự nhiên liên tiếp chia hết cho 2, cho 3.

    Suy ra phát biểu d) là đúng.

    Vậy phát biểu sai là b) và c).

    Bài 2 trang 19 SBT Toán 6 Tập 1: a) Tìm số tự nhiên a nhỏ hơn 10 để P = 15.16.17 + a vừa chia hết cho 3 vừa chia hết cho 10.

    b) Tìm số tự nhiên a lớn hơn 90 và nhỏ hơn 100 để 125 – a chia hết 5

    Lời giải

    a) Ta có 15 = 5.3 nên 15 chia hết cho 3. Suy ra 15.16.17 chia hết cho 3.

    Để P = 15.16.17 + a chia hết cho 3 thì a phải chia hết cho 3

    Mà a∈0;1;2;3;4;5;6;7;8;9

    ⇒a∈0;3;6;9 (1)

    Ta lại có 15.16.17 = 3.5.2.8.17 = 3.10.8.17 chia hết cho 10.

    Để P = 15.16.17 + a chia hết cho 10 thì a phải chia hết cho 10

    Mà a∈0;1;2;3;4;5;6;7;8;9

    ⇒a=0 (2)

    Từ (1) và (2) suy ra a = 0.

    Vậy với a = 0 để P = 15.16.17 + a vừa chia hết cho 3 vừa chia hết cho 10.

    b) Vì 125 có chữ số tận cùng là 5 nên 125 chia hết cho 5

    Để 125 – a chia hết 5 thì a chia hết cho 5

    Mà 90 < a < 100 nên a = 95

    Vậy a = 95.

    Bài 3 trang 19 SBT Toán 6 Tập 1: Cho B = 121 – 110 + 99 – 88 + … + 11 + 1.

    Không thực hiện phép tính, hãy cho biết B có chia hết cho 11 hay không.

    Lời giải

    Xét biểu thức B, ta có:

    121 = 11.11 chia hết cho 11

    110 = 11.10 chia hết cho 11

    99 = 11.9 chia hết cho 11

    88 = 11.8 chia hết cho 11

    …

    11 chia hết cho 11

    Do đó 121 - 110 + 99 - 88 + … + 11 chia hết cho 11

    Mà 1 không chia hết cho 11

    ⇒ biểu thức B có 1 số hạng không chia hết cho 11, các số hạng khác đều chia hết cho 11

    Vậy B không chia hết cho 11.

    Bài 4 trang 19 SBT Toán 6 Tập 1: Khi chia số tự nhiên M cho 12 ta được số dư là 10. Hỏi M có chia hết cho 2, cho 3, cho 4 hay không?

    Lời giải

    Vì M chia cho 12 dư 10, nên ta viết M = 12.q + 10.

    ⇒ M = 2.6.q + 2.5 = 2.(6q +5) chia hết cho 2

    Ta có:

    M = 3.4.q + 3.3 + 1 = 3.(4q + 3) + 1

    ⇒ M chia 3 dư 1.

    Do đó M không chia hết cho 3.

    M = 4.3.q + 4.2 + 2 = 4 (3q + 2) + 2

    ⇒ M chia 4 dư 2.

    Do đó M không chia hết cho 4.

    Vậy M chia hết cho 2 nhưng không chia hết cho 3 và cho 4

    Bài 5 trang 19 SBT Toán 6 Tập 1: Viết kết quả phép chia dưới dạng a = b.q + r, với 0≤r<b.

    a) 92 727:6 315;

    b) 589 142:1 093;

    c) 68 842: 6 329.

    Lời giải

    a)

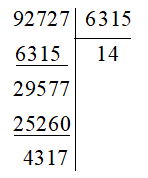
    Viết kết quả phép chia dưới dạng a = b.q + r, với 0 <= r < b (ảnh 1)

    Suy ra 92 727:6 315 = 14 dư 4317 nên ta viết được: 92 727 = 6 315.14 + 4 317.

    Vậy 92 727 = 6 315.14 + 4 317.

    b) 589 142:1 093

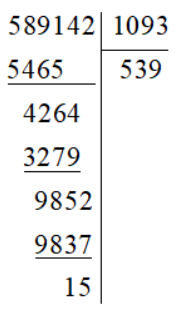
    Viết kết quả phép chia dưới dạng a = b.q + r, với 0 <= r < b (ảnh 1)

    Suy ra 589 142:1 093 = 539 dư 15 nên ta viết được: 589 142 = 1 093.539 + 15.

    Vậy 589 142 = 1 093.539 + 15.

    c)

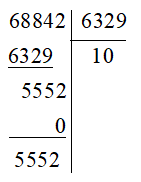
    Viết kết quả phép chia dưới dạng a = b.q + r, với 0 <= r < b (ảnh 1)

    Suy ra 68 842: 6 329 = 10 dư 5552 nên ta viết được: 68 842 = 10.6 329 + 5552.

    Vậy 68 842 = 10.6 329 + 5552.

    Xem thêm lời giải sách bài tập Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 7: Dấu hiệu chia hết cho 2, cho 5

    Bài 8: Dấu hiệu chia hết cho 3, cho 9

    Bài 9: Ước và bội

    Bài 10: Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố

    Bài 12: Ước chung. Ước chung lớn nhất

    Tham khảo các loạt bài Toán 6 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,226 15/03/2024
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: