Giải SBT Toán 6 (Chân trời sáng tạo) Bài tập cuối chương 9

Mục lục Giải SBT Toán 6 Bài tập cuối chương 9

Bài 1 trang 127 SBT Toán 6 Tập 2: Tổ 3 có 4 bạn An, Bình, Chính, Dương. Hãy liệt kê tất cả các khả năng có thể xảy ra của mỗi phép thử sau:

a) Chọn hai bạn thuộc tổ 3 đi trực nhật.

b) Chọn một bạn làm tổ trưởng, một bạn làm tổ phó tổ 3.

Lời giải:

a) Tất cả các khả năng có thể xảy ra của phép thử chọn ra hai bạn đi trực nhật là là An và Bình, An và Chính, An và Dương, Bình và Chính, Bình và Dương, Chính và Dương.

b) Ký hiệu tên các bạn An, Bình, Chính, Dương lần lượt là là A, B, C, D. Tất cả các khả năng có thể xảy ra của phép thử chọn ra một bạn tổ trưởng một bạn tổ phó là:

Bài 2 trang 127 SBT Toán 6 Tập 2: Trong hộp có 1 quả bóng xanh, 1 quả bóng đỏ và 1 quả bóng trắng. Chọn ra từ hộp 1 quả bóng. Hãy đánh giá xem các sự kiện sau là chắc chắn, không thể hay có thể xảy ra.

a) Bóng chọn ra có màu xanh.

b) Bóng chọn ra không có màu xanh.

c) Bóng chọn ra có màu vàng.

d) Bóng chọn ra không có màu tím.

Lời giải:

a) Chọn 1 quả bóng trong 3 quả bóng từ hộp thì quả bóng được chọn có thể là quả bóng màu xanh, màu đỏ hoặc màu trắng.

Vậy sự kiện “Bóng chọn ra có màu xanh’ có thể xảy ra.

b) Chọn 1 quả bóng trong 3 quả bóng từ hộp thì quả bóng được chọn có thể là quả bóng màu xanh, màu đỏ hoặc màu trắng.

Do đó có thể xảy ra trường hợp quả bóng chọn ra không có màu xanh.

Vậy sự kiện “Bóng chọn ra không có màu xanh” có thể xảy ra.

c) Sự kiện “Bóng chọn ra có màu vàng” không thể xảy ra. Vì trong số 3 quả bóng trong hộp không có quả bóng màu vàng.

d) Sự kiện “Bóng chọn ra không có màu tím” chắc chắn xảy ra. Vì trong số 3 quả bóng trong hộp không có quả bóng màu tím.

Bài 3 trang 127 SBT Toán 6 Tập 2: Trong hộp có 1 quả bóng xanh, 2 quả bóng đỏ và 3 quả bóng vàng. Thủy lấy ra 4 quả bóng từ hộp. Hỏi các sự kiện sau là chắc chắn, không thể hay có thể xảy ra?

a) Bốn bóng lấy ra có cùng màu.

b) Có ít nhất một bóng đỏ trong 4 bóng lấy ra.

c) Có ít nhất một bóng vàng trong 4 bóng lấy ra.

Lời giải:

a) Vì số lượng bóng cùng màu nhiều nhất là 3 quả (bóng vàng), nên không thể lấy ra được 4 quả cùng màu từ trong hộp.

Vậy sự kiện “4 bóng lấy ra có cùng màu” không thể xảy ra.

b) Nếu lấy ra 1 bóng xanh, 3 bóng vàng thì trong 4 quả bóng lấy ra không có quả bóng nào màu đỏ.

Mặt khác, nếu lấy ra 1 bóng xanh, 2 bóng vàng, 1 bóng đỏ thì trong 4 quả bóng lấy ra có 1 bóng đỏ.

Vậy sự kiện “Có ít nhất một bóng đỏ trong 4 bóng lấy ra” có thể xảy ra.

c) Vì tổng số bóng xanh và đỏ trong hộp là 3 quả, mà số quả lấy là 4 quả, nên chắc chắn sẽ có ít nhất là 1 quả bóng vàng trong 5 quả được lấy ra.

Vậy sự kiện “Có ít nhất một bóng vàng trong 4 bóng lấy ra” chắc chắn xảy ra.

Bài 4 trang 127 SBT Toán 6 Tập 2: Cảnh sát giao thông ghi lại số vụ va chạm giao thông trên một đoạn đường trong 30 ngày của tháng 6. Kết quả cho ở bảng sau:

Tính xác suất thực nghiệm của sự kiện:

a) Một ngày không có vụ va chạm giao thông nào.

b) Một ngày có nhiều hơn 1 vụ va chạm giao thông.

Lời giải:

a) Số ngày không có vụ vi phạm giao thông nào trong 30 ngày là: 16.

Vậy xác suất thực nghiệm của sự kiện “Một ngày không có vụ va chạm giao thông nào” là: $\frac{16}{30}=\frac{8}{15}.$

b) Số ngày có nhiều hơn 1 vụ va chạm giao thông là tổng số các ngày có 2 vụ, 3 vụ và 4 vụ va chạm giao thông.

Số ngày có 2 vụ va chạm giao thông là: 6.

Số ngày có 3 vụ va chạm giao thông là: 1.

Số ngày có 4 vụ va chạm giao thông là: 1.

Số ngày có nhiều hơn 1 vụ va chạm giao thông là: 6 + 1 + 1 = 8.

Vậy xác suất thực nghiệm của sự kiện “Một ngày có nhiều hơn 1 vụ va chạm giao thông” là: $\frac{8}{30}=\frac{4}{15}.$

Bài 5 trang 127, 128 SBT Toán 6 Tập 2: Gieo một con xúc xắc 6 mặt 100 lần ta được kết quả như sau:

Hãy tính xác suất thực nghiệm của sự kiện:

a) Gieo được mặt có 3 chấm.

b) Gieo được mặt có số chẵn chấm.

Lời giải:

a) Số lần xuất hiện mặt 3 chấm của con xúc xắc 6 mặt trong 100 lần gieo là: 19.

Vậy xác suất thực nghiệm của sự kiện “Gieo được mặt có 3 chấm” là: $\frac{19}{100}=\mathrm{0,19.}$

b) Số mặt có chẵn chấm là các mặt có 2 chấm, 4 chấm và 6 chấm.

Số lần xuất hiện mặt 2 chấm là: 14.

Số lần xuất hiện mặt 4 chấm là: 15.

Số lần xuất hiện mặt 6 chấm là: 19.

Do đó, số lần xuất hiện mặt có chẵn chấm của con xúc xắc 6 mặt trong 100 lần gieo là: 14 + 15 + 19 = 48.

Vậy xác suất thực nghiệm của sự kiện “Gieo được mặt có số chẵn chấm” là: $\frac{48}{100}=\mathrm{0,48.}$

Bài 6 trang 128 SBT Toán 6 Tập 2: Gieo đồng thời hai con xúc xắc 6 mặt 100 lần và xem có bao nhiêu mặt 6 chấm xuất hiện trong mỗi lần gieo. Kết quả thu được như sau:

Hãy tính xác suất thực nghiệm để:

a) Cả hai con xúc xắc đều xuất hiện mặt 6 chấm.

b) Có ít nhất một mặt 6 chấm xuất hiện.

Lời giải:

a) Số lần cả hai con xúc xắc đều xuất hiện mặt 6 chấm là 3.

Vậy xác suất thực nghiệm của sự kiện “Cả hai con xúc xắc đều xuất hiện mặt 6 chấm” là: $\frac{3}{100}=\mathrm{0,03.}$

b) Con xúc xắc có ít nhất một mặt 6 chấm xuất hiện, nghĩa là con xúc xắc có thể có một mặt hoặc hai mặt 6 chấm xuất hiện.

Số lần con xúc xắc có một mặt 6 chấm xuất hiện là 27.

Số lần con xúc xắc có hai mặt 6 chấm xuất hiện là 3.

Do đó số lần con xúc xắc có ít nhất 1 mặt 6 chấm xuất hiện trong 100 lần gieo là: 27 + 3 = 30.

Vậy xác suất thực nghiệm của sự kiện “Có ít nhất một mặt 6 chấm xuất hiện” là: $\frac{30}{100}=\mathrm{0,3.}$

Bài 7 trang 128 SBT Toán 6 Tập 2: Trong hộp có một số viên bi màu xanh, đỏ và vàng có kích thước giống nhau. Lấy ngẫu nhiên một viên bi từ hộp, xem màu rồi trả lại lại. Lặp lại hoạt động đó 50 lần ta được kết quả như sau:

a) Tính xác suất thực hiện của sự kiện “lấy được viên bi xanh”.

b) Em hãy dự đoán xem trong hộp loại bi nào có nhiều hơn.

Lời giải:

a) Số lần lấy được bi xanh trong 50 lần lấy bi từ hộp là 32.

Vậy xác suất thực nghiệm của sự kiện “lấy được viên bi xanh” trong 50 lần lấy là: $\frac{32}{50}=\mathrm{0,64.}$

b) Ta thấy: số lần lấy được viên bi xanh nhiều hơn so với số lần lấy được viên bi đỏ và viên bi vàng.

Vậy có thể dự đoán là trong hộp đó số viên bi xanh nhiều hơn số viên bi đỏ và số viên bi vàng.

Bài 8 trang 128 SBT Toán 6 Tập 2: Một nhà hàng thu phiếu phản hồi về độ hài lòng của một số khách hàng được lựa chọn ngẫu nhiên trong tháng 1. Kết quả thu được như sau:

a) Hãy tính xác suất thực nghiệm của sự kiện “khách hàng không hài lòng”.

b) Nhà hàng tiếp tục khảo sát trên trong tháng 2. Kết quả thu được như sau:

Hãy tính xác suất thực nghiệm của sự kiện “khách hàng không hài lòng” sau 2 tháng.

Độ hài lòng của khách hàng sau 2 tháng là tăng hay giảm?

Lời giải:

a) Số khách hàng không hài lòng trong tháng 1 là 5.

Tổng số phiếu phản hồi của khách hàng trong tháng 1 là: 5 + 15 + 10 = 30.

Vậy xác suất thực nghiệm của sự kiện “khách hàng không hài lòng” trong 30 phiếu đánh giá là: $\frac{5}{30}=\frac{1}{6}.$

b) Số khách hàng không hài lòng trong tháng 2 là 3.

Tổng số phiếu phản hồi của khách hàng trong tháng 2 là: 3 + 10 + 17 = 30.

Tổng số phiếu phản hồi của khách hàng sau 2 tháng là: 30 + 30 =60

Vậy xác suất thực nghiệm của sự kiện “khách hàng không hài lòng” sau 2 tháng là: $\frac{8}{60}=\frac{2}{15}.$

Vì $\frac{1}{6}>\frac{2}{15}$ nên độ không hài lòng của khách hàng giảm, tức là độ hài lòng của khách hàng có tăng lên.

Bài 9 trang 129 SBT Toán 6 Tập 2: Kết quả điều tra về môn học được yêu thích nhất của các bạn lớp 6A được thể hiện trong bảng sau đây:

a) Số bạn tham gia trả lời trong cuộc điều tra là bao nhiêu?

b) Đơn vị và dấu hiệu điều tra ở đây là gì? Dấu hiệu điều tra nhận những giá trị nào?

c) Lập bảng và biểu đồ cột thống kê số lượng các bạn yêu thích mỗi môn học.

d) Tính xác suất thực nghiệm của sự kiện bạn được phỏng vấn yêu thích môn Mỹ thuật nhất dựa trên số liệu điều tra trên.

Lời giải:

a) Số bạn tham gia cuộc điều tra là 35 bạn.

b) Đơn vị điều tra là học sinh.

Dấu hiệu điều tra là môn học yêu thích nhất của mỗi học sinh.

Dấu hiệu điều tra nhận các giá trị là: Toán, Ngữ văn, Tiếng Anh, Mỹ Thuật, Âm nhạc.

c) Bảng thống kê số bạn yêu mỗi môn học:

Biểu đồ cột thống kê số lượng các bạn yêu thích mỗi môn học:

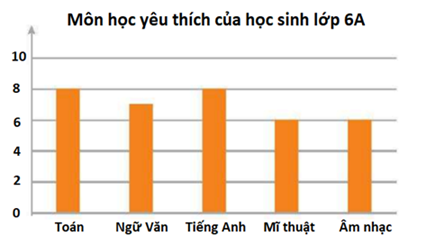
d) Số bạn yêu thích môn Mĩ thuật trong 35 bạn là 6.

Xác suất thực nghiệm của sự kiện bạn được phỏng vấn yêu thích môn Mỹ thuật là: $\frac{6}{35}.$

Xem thêm lời giải sách bài tập Toán lớp 6 sách Chân trời sáng tạo hay, chi tiết khác:

Bài 6: Góc

Bài 7: Số đo góc. Các góc đặc biệt

Bài tập cuối chương 8

Bài 1: Phép thử nghiệm - Sự kiện

Bài 2: Xác suất thực nghiệm