Nội dung bài viết

    Xem thêm

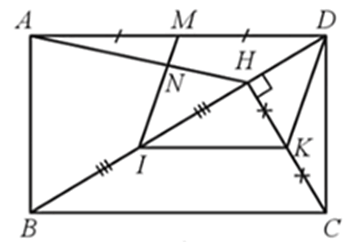
    Cho hình chữ nhật ABCD. Kẻ CH vuông góc với BD (H thuộc BD). Gọi I, K, M lần lượt là

    Lời giải Bài 18 trang 66 SBT Toán 8 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8.

    1 1,147 14/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 3: Đường trung bình của tam giác

    Bài 18 trang 66 SBT Toán 8 Tập 2: Cho hình chữ nhật ABCD. Kẻ CH vuông góc với BD (H ∈ BD). Gọi I, K, M lần lượt là trung điềm của BH, CH, AD. Chứng minh:

    a) Tứ giác IKDM là hình bình hành;

    b) Gọi N là giao điểm của IM và AH. Hỏi IN có thể là đường trung bình của tam giác HAB không? Vì sao?

    Lời giải:

    Cho hình chữ nhật ABCD. Kẻ CH vuông góc với BD (H ∈ BD). Gọi I, K, M lần lượt

    a) Xét ∆HBC có I, K lần lượt là trung điểm của BH, CH nên IK là đường trung bình của ∆HBC

    Suy ra IK // BC và IK=BC2.

    Do ABCD là hình chữ nhật nên AD // BC, AD = BC, mà M ∈ AD nên MD // BC

    Do đó, IK // MD (1)

    Vì IK=BC2 và MD=BC2 (do M là trung điểm của AD, AD = BC) nên IK = MD (2)

    Từ (1) và (2) suy ra tứ giác IKDM là hình bình hành.

    b) Nếu IN là đường trung bình của tam giác HAB thì IN // AB. Suy ra IM // AB.

    Xét ∆ABD có M là trung điểm của AD và IM // AB nên I là trung điểm của BD (3).

    Mặt khác, theo giả thiết, I là trung điểm của HB (4).

    Từ (3) và (4) suy ra vô lí.

    Vậy IN không thể là đường trung bình của tam giác HAB.

    Xem thêm lời giải SBT Toán lớp 8 bộ sách Cánh diều hay, chi tiết khác:

    Bài 14 trang 65 SBT Toán 8 Tập 2: Chọn phát biểu đúng trong các phát biểu sau:...

    Bài 15 trang 65 SBT Toán 8 Tập 2: Hình 21 cho biết cạnh của tam giác đều ABC bằng 6 cm;...

    Bài 16 trang 65 SBT Toán 8 Tập 2: Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC...

    Bài 17 trang 65 SBT Toán 8 Tập 2: Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân ABC...

    Bài 18 trang 66 SBT Toán 8 Tập 2: Cho hình chữ nhật ABCD. Kẻ CH vuông góc với BD (H ∈ BD)....

    Bài 19* trang 66 SBT Toán 8 Tập 2: Cho tứ giác ABCD có AD = BC. Đường thẳng đi qua trung điểm M và N...

    Bài 20* trang 66 SBT Toán 8 Tập 2: Cho tứ giác ABCD có M, N lần lượt là trung điểm của AD, BC....

    Xem thêm lời giải SBT Toán lớp 8 bộ sách Cánh diều hay, chi tiết khác:

    Bài 4: Tính chất đường phân giác của tam giác

    Bài 5: Tam giác đồng dạng

    Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

    Bài 7: Trường hợp đồng dạng thứ hai của tam giác

    Bài 8: Trường hợp đồng dạng thứ ba của tam giác

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,147 14/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: