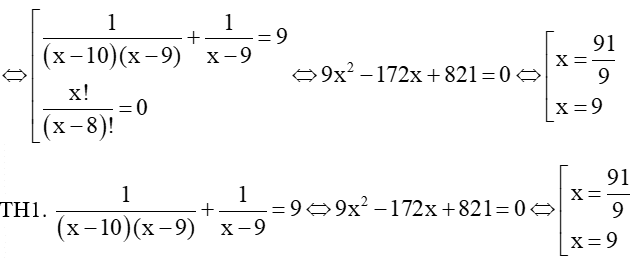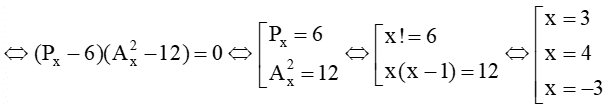TOP 30 câu Trắc nghiệm Ôn tập chương 5 (Cánh diều 2024) có đáp án - Toán 10

Đáp án đúng là: B

Ta có (a + b)⁵ = a⁵ + 5a⁴b +10a³b² + 10a²b³ + 5ab⁴ + b⁵

Do đó: (5 – 2x)⁵ = 5⁵ + 5.5⁴.(– 2x) + 10.5³.(– 2x) ² + 10.5².(– 2x)³ + 5.5.(– 2x)⁴ + (– 2x)⁵

= 3 125 – 6 250x + 5 000x² – 2 000x³ + 400x⁴ – 32x⁵

= – 32x⁵ + 400x⁴ – 2 000x³ + 5 000x² – 6 250x + 3 125

Hệ số của x⁵ trong khai triển là – 32.

Đáp án đúng là: A

Vì chọn 3 quả cầu có đủ 3 màu nên mỗi màu ta chọn một quả

Quả cầu đỏ có 7 cách chọn

Quả cầu vàng có 5 cách chọn

Quả cầu trắng có 3 cách chọn

Vậy có 7.5.3 = 105 cách.

Đáp án đúng là: B

Gọi số tự nhiên có 4 chữ số cần tìm là: $\overline{abcd}$ (a ≠ 0), khi đó:

a có 4 cách chọn (vì a có thể chọn tuỳ ý một trong 4 số 5; 6; 7; 8)

b có 4 cách chọn (vì b ≠ a nên b không được chọn lại số mà a đã chọn vậy b có 4 số để chọn)

c có 3 cách chọn (vì c ≠ a, c ≠ b nên c không được chọn lại số mà a, b đã chọn vậy c còn 3 số để chọn)

d có 2 cách chọn (vì d ≠ a, d ≠ b, d ≠ c nên d không được chọn lại số mà a, b, c đã chọn vậy c còn 2 số để chọn)

Vậy có: 4.4.3.2 = 96 số

Đáp án đúng là: C

Gọi số tự nhiên có 3 chữ số cần tìm là: $\overline{abc}$ (a ≠ 0) khi đó:

c có 3 cách chọn (vì $\overline{abc}$ là số lẻ nên c có thể chọn 1 trong 3 số 3; 5; 7)

a có 6 cách chọn (vì a có thể chọn tuỳ ý một trong 6 số 2; 3; 4; 5; 6; 7)

b có 7 cách chọn (vì b có thể chọn tuỳ ý một trong 7 số 0; 2; 3; 4; 5; 6; 7)

Vậy có: 3.6.7 = 126 số.

Đáp án đúng là: D

Gọi số tự nhiên cần tìm có dạng $\overline{abc}$ (a ≠ 0) Khi đó:

a có 4 cách chọn (vì a là số chẵn và a ≠ 0 nên a chỉ được chọn một trong 4 số 2; 4; 6; 8)

b có 5 cách chọn (vì b là số chẵn nên b chỉ được chọn một trong 5 số 0; 2; 4; 6; 8)

c có 5 cách chọn (vì c là số chẵn nên c chỉ được chọn một trong 5 số 0; 2; 4; 6; 8)

Vậy ta có: 4.5.5 = 100 số

Đáp án đúng là: C

Điều kiện n ≥ 2; n $\in$ℕ.

Ta có $A_n^2+2C_n^n=22$$\iff \frac{n!}{\left(n-2\right)!}+2=22$

$\iff$ n(n – 1) = 20

$\iff$n = 5 hoặc n = – 4

Kết hợp với điều kiện n = 5 thoả mãn

Ta có (a + b)⁵ = a⁵ + 5a⁴b +10a³b² + 10a²b³ + 5ab⁴ + b⁵

Thay a = 3x; b = – 4 vào công thức ta có:

(3x – 4)⁵ = (3x)⁵ + 5(3x)⁴.(– 4) +10.(3x)³(– 4)² + 10.(3x)²(– 4)³ + 5(3x)(– 4)⁴ + (– 4)⁵

= 243x⁵ – 1620x⁴ + 4 320x³ – 5 760x² + 3 840x – 1 024

Vậy hệ số của x³ là 4 320.

Đáp án đúng là: B

Điều kiện n ≥ 3; n $\in$ ℕ

Ta có $A_n^3+5A_n^2=2\left(n+15\right)$ $\iff \frac{n!}{\left(n-3\right)!}+5.\frac{n!}{\left(n-2\right)!}=2\left(n+15\right)$.

$\iff$ n(n – 1)(n – 2) + 5n(n – 1) = 2(n + 15)

$\iff$ n³ + 2n² – 5n – 30 = 0

$\iff$ (n – 3)(n² + 5n + 10) = 0

$\iff$ n = 3 (vì n² + 5n + 10 > 0 với mọi n)

Vậy có 1 giá tri của n thoả mãn điều kiện.

Đáp án đúng là: C

Gọi số có ba chữ số cần tìm là $\overline{abcd}$, với a ≠ 0

a có 6 cách chọn (vì a ≠ 0 nên a có thể chọn một trong 6 số 1; 2; 3; 4; 5; 6)

b có 7 cách chọn (vì b có thể chọn tuỳ ý một trong 7 số 0; 1; 2; 3; 4; 5; 6)

c có 7 cách chọn (vì c có thể chọn tuỳ ý một trong 7 số 0; 1; 2; 3; 4; 5; 6)

d có 4 cách chọn (vì $\overline{abcd}$ là số chẵn nên d phải là số chẵn vậy d chỉ được chọn một trong 4 số 0; 2; 4; 6)

Vậy số các số cần tìm là 6.7.7.4 = 1176 (số).

Đáp án đúng là: A

Gọi số tự nhiên chẵn có 4 chữ số cần tìm là: $\overline{abcd}$ (a ≠ 0) khi đó:

d có 3 cách chọn (vì số tự nhiên chẵn nên d có thể chọn một trong 3 số 2; 4; 6)

a có 5 cách chọn (vì a có thể chọn tuỳ ý một trong 5 số 2; 3; 4; 5; 6)

b có 5 cách chọn (vì b có thể chọn tuỳ ý một trong 5 số 2; 3; 4; 5; 6)

c có 5 cách chọn (vì c có thể chọn tuỳ ý một trong 5 số 2; 3; 4; 5; 6)

Vậy có: 3.5.5.5 = 375 số.

Đáp án đúng là: B

Điều kiện: x ≥ 10; x $\in$ ℕ

Ta có $A_x^{10}+A_x^9=9A_x^8\iff \frac{x!}{\left(x-10\right)!}+\frac{x!}{\left(x-9\right)!}=9.\frac{x!}{\left(x-8\right)!}$

$\iff \frac{x!}{\left(x-8\right)!}\left(\frac{1}{\left(x-10\right)(x-9)}+\frac{1}{x-9}\right)=9.\frac{x!}{\left(x-8\right)!}$

Kết hợp với điều kiện ta được x = 9 thoả mãn.

TH2. $\frac{x!}{\left(x-8\right)!}=0$

Vì x ≥ 10 nên $\frac{x!}{\left(x-8\right)!}\ne 0$

Vậy x = 9.

Đáp án đúng là: D

Mỗi cách xếp 20 thí sinh vào 20 vị trí của một phòng thi là một hoán vị của 20 phần tử, vậy số cách xếp là 20! cách.

Đáp án đúng là: B

Ta có (a + b)⁵ = a⁵ + 5a⁴b +10a³b² + 10a²b³ + 5ab⁴ + b⁵

Do đó: (2x + 3)⁵ = (2x)⁵ + 5(2x)⁴.3 +10(2x)³.3² + 10(2x)².3³ + 5.(2x).3⁴ + 3⁵

= 32x⁵ + 240x⁴ + 720x³ + 1 080x² + 810x + 243

Vậy trong khai triển số hạng chứa x⁴ là 240x⁴.

Đáp án đúng là: A

Điều kiện n ≥ 2; n $\in$ℕ

Ta có $A_n^2=210$$\iff \frac{n!}{\left(n-2\right)!}=210$

$\iff$ n(n – 1) = 210$\iff$ n² – n – 210 = 0

$\iff$ n = 15 hoặc n = –14

Kết hợp với điều kiện n = 15 thoả mãn.

Đáp án đúng là: C

Ta có $3A_n^2-A_{2n}^2+42=0$ $\iff 3.\frac{n!}{\left(n-2\right)!}-\frac{\left(2n\right)!}{\left(2n-2\right)!}+42=0$

$\iff$ 3n(n – 1) – 2n(2n – 1) + 42 = 0

$\iff$ - n² – n + 42 = 0

$\iff$ n = 6 hoặc n = – 7

Kết hợp với điều kiện n = 6 thoả mãn.

Đáp án đúng là: B

Điều kiện: x ≥ 2; x $\in$ ℕ

Phương trình $P_x{A}_x^2+72=6(A_x^2+2P_x)$$\iff A_x^2\left(P_x-6\right)-12(P_x-6)=0$

Kết hợp với điều kiện x = 3; x = 4 thoả mãn. Vậy có 2 giá trị của x.

Đáp án đúng là: B

Ta có: (a + b)⁴ = a⁴ + 4a³b + 5a²b² + 4ab³ + b⁴.

Do đó (1 + 2x)⁴ = 1⁴ + 4.1³.(2x) + 5.1².(2x)² + 4.1.(2x)³ + (2x)⁴

= 1 + 8x + 20x² + 24x³ + 16x⁴

Suy ra hệ số của x³ là 24 và hệ số của x² là 20. Khi đó ta có tổng hai hệ số bằng 24 + 20 = 44.

Đáp án đúng là: B

Khai triển nhị thức

(x + y)⁴ = $C_4^0$(x)⁴(y)⁰ + $C_4^1$(x)³(y)¹ + $C_4^2$(x)²(y)² + $C_4^3$(x)(y)³ + $C_4^4$(x)⁰(y)⁴

= x⁴ + 4x³y + 6x²y² + 6xy³ + y⁴.

Đáp án đúng là: C

Giả sử các tiết mục được biểu diễn đánh số thứ tự từ 1 đến 8. Vì số lượng tiết mục hát và múa bằng nhau nên có hai trường hợp:

Trường hợp 1: Tiết mục hát diễn ra đầu tiên

Khi đó, các tiết mục hát có số thứ tự là số lẻ, còn các tiết mục múa có số thứ tự là số chẵn. Như vậy, thứ tự của các tiết mục múa và hát được cố định, chỉ thay đổi thứ tự giữa các tiết mục múa, hoặc giữa các tiết mục hát.

Chọn 4 tiết mục hát từ 6 tiết mục hát và xếp thứ tự có:

$A_6^4=360$ (cách)

Chọn 4 tiết mục múa từ 5 tiết mục múa và xếp thứ tự có:

$A_5^4=120$ (cách)

Khi đó, số cách chọn và xếp thứ tự các tiết mục văn nghệ trong trường hợp tiết mục hát diễn ra đầu tiên là:

360.120 = 43 200

Trường hợp 2: Tiết mục múa diễn ra đầu tiên

Tương tự, số cách chọn và xếp thứ tự các tiết mục văn nghệ trong trường hợp tiết mục múa diễn ra đầu tiên là:

120.360 = 43 200

Vậy số cách chọn và xếp thứ tự các tiết mục văn nghệ sao cho các tiết mục hát và múa xen kẽ nhau là:

43 200 + 43 200 = 86 400.

Đáp án đúng là: D

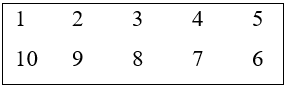
Ta đánh số liên tiếp 12 chỗ ngồi bằng các số từ 1 đến 6 thuộc một dãy và từ 7 đến 12 thuộc một dãy như sau:

Để xếp vị trí ta có các cách chọn như sau:

Vậy có: 460800 cách xếp.

Đáp án đúng là: D

Gọi số vận động viên nam là n.

Số ván các vận động viên nam chơi với nhau là $2.C_n^2=n\left(n-1\right)$.

Số ván các vận động viên nam chơi với các vận động viên nữ là $\mathrm{2.2.}n=4n$

Vậy ta có n(n – 1) – 4n = 84

$\iff$ n² – 5n – 84 = 0

$\iff$n = 12 hoặc n = – 7.

Kết hợp với điều kiện n = 12 thoả mãn

Vậy số ván các vận động viên chơi là $2C_{14}^2=182$.

Đáp án đúng là: D

Số cách xếp 3 cổ động viên mặc áo vàng là: 3! cách

Số cách xếp 4 cổ động viên mặc áo đỏ là: 4! cách

Số cách xếp 5 cổ động viên mặc áo xanh là: 5! cách

Hoán đổi vị trí của 3 nhóm cổ động viên có 3! cách

Vậy số cách xếp thỏa yêu cầu đề bài bằng 3!.3!.4!.5! = 103680 cách.

Đáp án đúng là: C

Đa giác có n cạnh $\left(n\in \mathbb{N},n\ge 3\right)$.

Số đường chéo trong đa giác là: $C_n^2-n$.

Vì số đường chéo gấp đôi số cạnh nên ta có

$C_n^2-n=2n\iff \frac{n!}{\left(n-2\right)!.2!}=3n$

⇒ n(n – 1) = 6n

⇒ n = 7 hoặc n = 0

Kết hợp với điều kiện n = 7 thoả mãn.

Đáp án đúng là: D

Điều kiện: 0 ≤ n ≤ 5; n $\in$ℕ.

$\frac{5}{C_5^n}-\frac{2}{C_6^n}=\frac{14}{C_7^n}$$\iff \frac{5}{\frac{5!}{\left(5-n\right)!n!}}-\frac{2}{\frac{6!}{\left(6-n\right)!n!}}=\frac{14}{\frac{7!}{\left(7-n\right)!n!}}$

$\iff \frac{5.\left(5-n\right)!n!}{5!}-\frac{2.\left(6-n\right)!n!}{6!}=\frac{14.\left(7-n\right)!n!}{7!}$

$\iff$ 5.6.7 – 2.7.(6 – n) = 14.(6 – n)(7 – n)

$\iff$14n² – 196n + 462 = 0

$\iff$n = 11 hoặc n = 3

Kết hợp với điều kiện n = 3 thoả mãn.

Đáp án đúng là: B

Ta có: (2x – 3)³ = (2x)³ + 2.(2x)².(– 3) + 2.(2x).(– 3)² + (– 3)³ = 8x³ – 24x² + 36x – 27.

Hệ số của x² là k = – 24.

Vậy k là một số nguyên âm.

Đáp án đúng là: D

Số đường chéo là $C_n^2-n$.

+ Đa giác đã cho có 135 đường chéo nên $C_n^2-n=135$.

$\iff$ $\frac{n!}{\left(n-2\right)!2!}-n=135$

$\iff$n(n – 1) – 2n = 270

$\iff$n² – 3n – 270 = 0

$\iff$n = 18 hoặc n = – 15

Kết hợp với điều kiện n = 18 thoả mãn.

Đáp án đúng là: D

Vì trong 2n điểm đã cho không có 3 điểm nào thẳng hàng nên cứ 3 điểm tạo thành một mặt phẳng, thế thì ta có $C_{2n}^3$ mặt phẳng.

Tuy nhiên vì trong 2n điểm đó có đúng n điểm cùng nằm trên mặt phẳng nên n điểm này có duy nhất 1 mặt phẳng.

Vậy số mặt phẳng có được là $\left(C_{2n}^3-C_n^3+1\right)$.

Theo đề bài ta có: $C_{2n}^3-C_n^3+1=505$ $\iff \frac{\left(2n\right)!}{3!\left(2n-3\right)!}-\frac{n!}{3!\left(n-3\right)!}=504$

$\iff$2n(2n – 1)(2n – 2) – n(n – 1)(n – 2) = 3024

$\iff$7n³ – 9n² + 2n – 3024 = 0

$\iff$ n = 8 (thỏa mãn điều kiện)

Vậy n = 8.

Đáp án đúng là D

Ta có $A_n^k=\frac{n!}{(n-k)!}=n\left(n-1\right)\mathrm{...}\left(n-k+1\right)$. Do đó A đúng và D sai.

Ta lại có: P_n = n! = n(n – 1)(n – 2)...2.1.

Đáp án đúng là:A

Ta có (a + b)⁵ = a⁵ + 5a⁴b +10a³b² + 10a²b³ + 5ab⁴ + b⁵

Do đó: (x + 2y)⁵ = x⁵ + 5.x⁴.(2y) + 10.x³.(2y)² + 10.x².(2y)³ + 5.x.(2y)⁴ + (2y)⁵

= x⁵ + 10x⁴.y + 40x³.y² + 80x².y³ + 80x.y⁴ + 32y⁵

Số hạng cần tìm chứa x²y⁵ nên ta có 80x²y³

Đáp án đúng là: D

Ta có khai triển

(2a + 1)⁵ = $C_5^0$(2a)⁵(1)⁰ + $C_5^1$(2a)⁴(1)¹ + $C_5^2$(2a)³(1)² + $C_5^3$(2a)²(1)³ + $C_5^4$(2a)(1)⁴ + $C_5^5$(2a)⁰(1)⁵ = 32a⁵ + 80a⁴ + 80a³ + 40a² + 10a + 1

Vậy 3 số hạng đầu của khai triển là 32a⁵ + 80a⁴ + 80a³

Đáp án đúng là: B

Gọi số tự nhiên có ba chữ số khác nhau là $\overline{abc}$ (a ≠ 0). Do số cần lập là số chẵn và phải có mặt chữ số 2 nên ta có các trường hợp.

Trường hợp 1: a = 2 khi đó số có dạng $\overline{2bc}$.

Chọn c có 2 cách (vì c ≠ 2 và $\overline{abc}$ là số chẵn nên c chọn được một trong các số 0; 8)

Chọn b có 4 cách (vì b ≠ 2 và b ≠ c nên b được chọn một trong các số 0; 1; 3; 5; 8 nhưng bỏ đi số mà c đã chọn)

Theo quy tắc nhân có 4.2 = 8 số.

Trường hợp 2: b = 2 và c = 0 khi đó số có dạng $\overline{a20}$.

Chọn a có 4 cách (vì a ≠ 2, a ≠ 0 nên a được chọn một trong các số 1; 3; 5; 8)

Theo quy tắc nhân có 1.1.4 = 4 số.

Trường hợp 3: b = 2 và c = 8 khi đó số có dạng $\overline{a28}$.

Chọn a có 3 cách (vì a ≠ 2 và a ≠ 0 nên a được chọn một trong các số 1; 3; 5)

Theo quy tắc nhân có 1.1.3 = 3 số.

Trường hợp 4: c = 2 khi đó số có dạng $\overline{ab2}$.

Chọn a có 4 cách (vì a ≠ 2 và a ≠ 0 nên a chọn được một trong các số 1; 3; 5; 8)

Chọn b có 4 cách (vì b ≠ 2 và b ≠ a nên b được chọn một trong các số 0; 1; 3; 5; 8 nhưng bỏ đi số mà a đã chọn)

Theo quy tắc nhân có 1.4.4 = 16 số.

Theo quy tắc cộng có 8 + 4 + 3 + 6 = 21 (số).