TOP 15 câu Trắc nghiệm Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác (Cánh diều 2024) có đáp án - Toán 10

Bộ 15 câu hỏi trắc nghiệm Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác có đáp án đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 1.

1 403 04/01/2024

Mua tài liệu

Trang trước

Trang sau

Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 10 Cánh diều bản word (cả năm) có đáp án chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Trắc nghiệm Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác - Cánh diều

Câu 1. Tam giác ABC có $A B = 2, A C = 1$ và $\hat{A} = 60 °$ . Tính độ dài cạnh BC.

A. BC = 1;

B. BC = 2;

C. BC = $\sqrt{2}$ ;

D. BC = $\sqrt{3}$

Hiển thị đáp án

Đáp án đúng là: D

Theo định lí hàm cosin, ta có:

$B C^{2} = A B^{2} + A C^{2} - 2 A B . A C . \cos \hat{A} = 2^{2} + 1^{2} - 2.2.1. \cos 60 ° = 3 \Rightarrow B C = \sqrt{3}$

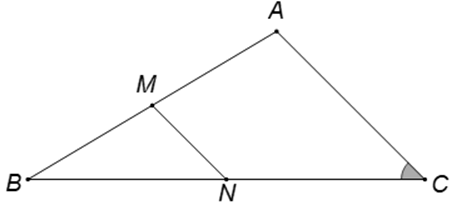
Câu 2. Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh

AB = 9 và $\hat{A C B} = 60 °$ . Tính độ dài cạnh cạnh BC.

A. $B C = 3 + 3 \sqrt{6};$

B. $B C = 3 \sqrt{6} - 3;$

C. $B C = 3 \sqrt{7};$

D. $B C = \frac{3 + 3 \sqrt{33}}{2} .$

Hiển thị đáp án

Đáp án đúng là: A

15 Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Gọi M, N lần lượt là trung điểm của AB, BC.

$\Rightarrow$ MN là đường trung bình của $Δ A B C$ .

$\Rightarrow M N = \frac{1}{2} A C$ . Mà MN = 3, suy ra AC = 6.

Theo định lí hàm cosin, ta có:

$A B^{2} = A C^{2} + B C^{2} - 2. A C . B C . \cos \hat{A C B}$

$\Leftrightarrow 9^{2} = 6^{2} + B C^{2} - 2.6. B C . \cos 60 °$

$\Leftrightarrow$ $B C^{2}$ - 6.BC - 45 = 0

$\Leftrightarrow$ BC = 3 + 3 $\sqrt{6}$

Câu 3. Tam giác ABC có $A B = \sqrt{2}, A C = \sqrt{3}$ và $\hat{C} = 45 °$ . Tính độ dài cạnh BC.

A. $B C = \sqrt{5};$

B. $B C = \frac{\sqrt{6} + \sqrt{2}}{2};$

C. $B C = \frac{\sqrt{6} - \sqrt{2}}{2};$

D. $B C = \sqrt{6} .$

Hiển thị đáp án

Đáp án đúng là: B

Theo định lí hàm cosin, ta có:

$A B^{2} = A C^{2} + B C^{2} - 2. A C . B C . \cos \hat{C}$

$\Rightarrow {(\sqrt{2})}^{2} = {(\sqrt{3})}^{2} + B C^{2} - 2. \sqrt{3} . B C . \cos 45 °$

$\Rightarrow$ $B C^{2}$ - $\sqrt{6}$ .BC + 1 = 0

$\Rightarrow B C = \frac{\sqrt{6} + \sqrt{2}}{2}$ .

Câu 4. Tam giác ABC có $A B = 5, B C = 7, C A = 8$ . Số đo góc $\hat{A}$ bằng:

A. $30 °;$

B. $45 °;$

C. $60 °;$

D. $90 ° .$

Hiển thị đáp án

Đáp án đúng là: C

Theo định lí hàm cosin, ta có: $\cos \hat{A} = \frac{A B^{2} + A C^{2} - B C^{2}}{2 A B . A C} = \frac{5^{2} + 8^{2} - 7^{2}}{2.5.8} = \frac{1}{2}$

Do đó, $\hat{A} = 60 °$ .

Câu 5. Tam giác ABC có $\hat{B} = 60 °, \hat{C} = 45 °$ và AB = 5. Tính độ dài cạnh AC.

A. $A C = \frac{5 \sqrt{6}}{2};$

B. $A C = 5 \sqrt{3};$

C. $A C = 5 \sqrt{2};$

D. AC = 10

Hiển thị đáp án

Đáp án đúng là: A

Theo định lí hàm sin, ta có:

$\frac{A B}{\sin \hat{C}} = \frac{A C}{\sin \hat{B}} \Leftrightarrow \frac{5}{\sin 45 °} = \frac{A C}{\sin 60 °} \Rightarrow A C = \frac{5 \sqrt{6}}{2}$ .

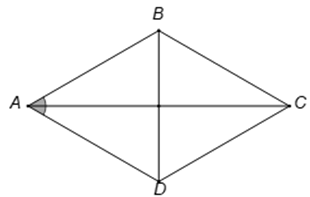
Câu 6. Cho hình thoi ABCD cạnh bằng 1cm và có $\hat{B A D} = 60 °$ . Tính độ dài AC.

A. $A C = \sqrt{3};$

B. $A C = \sqrt{2};$

C. $A C = 2 \sqrt{3};$

D. AC = 2.

Hiển thị đáp án

Đáp án đúng là: A

15 Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Do ABCD là hình thoi, có $\hat{B A D} = 60 ° \Rightarrow \hat{A B C} = 120 °$ .

Theo định lí hàm cosin, ta có:

$A C^{2} = A B^{2} + B C^{2} - 2. A B . B C . \cos \hat{A B C}$

$\Rightarrow 1^{2} + 1^{2} - 2.1.1. \cos 120 ° = 3 \Rightarrow A C = \sqrt{3}$

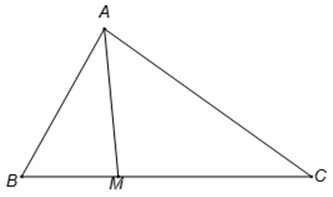
Câu 7. Tam giác ABC có $A B = 4, B C = 6, A C = 2 \sqrt{7}$ . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM..

A. $A M = 4 \sqrt{2};$

B. $A M = 3;$

C. $A M = 2 \sqrt{3};$

D. $A M = 3 \sqrt{2} .$

Hiển thị đáp án

Đáp án đúng là: C

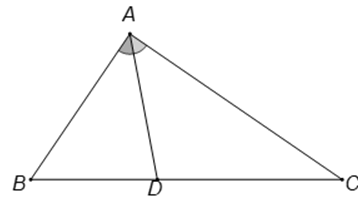
15 Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Theo định lí hàm cosin, ta có : $\cos B = \frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C} = \frac{4^{2} + 6^{2} - {(2 \sqrt{7})}^{2}}{2.4.6} = \frac{1}{2}$

Do $M C = 2 M B \Rightarrow B M = \frac{1}{3} B C = 2$ .Theo định lí hàm cosin, ta có:

$A M^{2} = A B^{2} + B M^{2} - 2. A B . B M . \cos \hat{B}$

$\Rightarrow 4^{2} + 2^{2} - 2.4.2. \frac{1}{2} = 12 \Rightarrow A M = 2 \sqrt{3}$

Câu 8. Tam giác ABC có $A B = \frac{\sqrt{6} - \sqrt{2}}{2}, B C = \sqrt{3}, C A = \sqrt{2}$ . Gọi D là chân đường phân giác trong góc $\hat{A}$ . Khi đó góc $\hat{A D B}$ bằng bao nhiêu độ?

A. $45 °;$

B. $60 °;$

C. $75 °;$

D. $90 ° .$

Hiển thị đáp án

Đáp án đúng là: C

15 Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Theo định lí hàm cosin, ta có:

$\cos \hat{B A C} = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} = - \frac{1}{2}$

$\Rightarrow \hat{B A C} = 120 ° \Rightarrow \hat{B A D} = 60 °$

$\cos \hat{A B C} = \frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C} = \frac{\sqrt{2}}{2} \Rightarrow \hat{A B C} = 45 °$

Trong $Δ A B D$ có $\hat{B A D} = 60 °, \hat{A B D} = 45 ° \Rightarrow \hat{A D B} = 75 °$ .

Câu 9. Tam giác ABC có $A B = 3, A C = 6$ và $\hat{A} = 60 °$ . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

A. R = 3

B. $R = 3 \sqrt{3}$ ;

C. $R = \sqrt{3};$

D. R = 6.

Hiển thị đáp án

Đáp án đúng là: A

Áp dụng định lí Cosin, ta có: $B C^{2} = A B^{2} + A C^{2} - 2 A B . A C . \cos \hat{B A C}$

$= 3^{2} + 6^{2} - 2.3.6. c o s 60^{0} = 27 \Leftrightarrow B C^{2} = 27 \Leftrightarrow B C^{2} + A B^{2} = A C^{2} .$

Suy ra tam giác ABC vuông tại B do đó bán kính $R = \frac{A C}{2} = 3.$

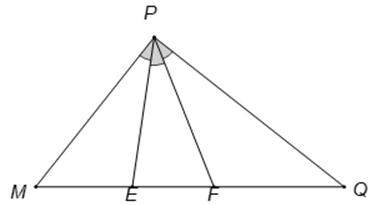
Câu 10. Tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc $\hat{M P E}, \hat{E P F}, \hat{F P Q}$ bằng nhau. Đặt $M P = q, P Q = m, P E = x, P F = y$ . Trong các hệ thức sau, hệ thức nào đúng?

A. $M E = E F = F Q;$

B. $M E^{2} = q^{2} + x^{2} - x q;$

C. $M F^{2} = q^{2} + y^{2} - y q;$

D. $M Q^{2} = q^{2} + m^{2} - 2 q m .$

Hiển thị đáp án

Đáp án đúng là: C

15 Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Ta có: $\hat{M P E} = \hat{E P F} = \hat{F P Q} = \frac{\hat{M P Q}}{3} = 30 ° \Rightarrow \hat{M P F} = \hat{E P Q} = 60 °$ .

Theo định lí hàm cosin, ta có:

$M E^{2} = M P^{2} + P E^{2} - 2. M P . P E . \cos \hat{M P E}$

$\Rightarrow q^{2} + x^{2} - 2 q x . \cos 30 ° = q^{2} + x^{2} - q x \sqrt{3}$

$M F^{2} = M P^{2} + P F^{2} - 2 M P . P F . \cos \hat{M P F}$

$\Rightarrow q^{2} + y^{2} - 2 q y . \cos 60 ° = q^{2} + y^{2} - q y$

$M Q^{2} = M P^{2} + P Q^{2} = q^{2} + m^{2}$

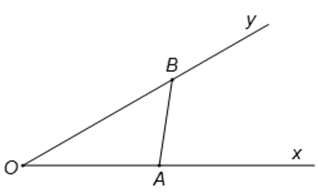
Câu 11. Cho góc $\hat{x O y} = 30 °$ . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:

A. $\frac{3}{2};$

B. $\sqrt{3};$

C. $2 \sqrt{2};$

D. 2.

Hiển thị đáp án

Đáp án đúng là: D

Theo định lí hàm sin, ta có:

$\frac{O B}{\sin \hat{O A B}} = \frac{A B}{\sin \hat{A O B}} \Leftrightarrow O B = \frac{A B}{\sin \hat{A O B}} . \sin \hat{O A B}$

$\Leftrightarrow \frac{1}{\sin 30 °} . \sin \hat{O A B} = 2 \sin \hat{O A B}$

Do đó, độ dài OB lớn nhất khi và chỉ khi

$\sin \hat{O A B} = 1 \Leftrightarrow \hat{O A B} = 90 °$

Khi đó OB = 2.

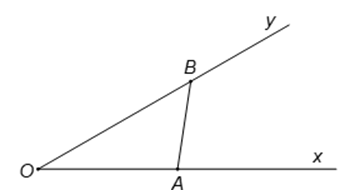
Câu 12. Cho góc $\hat{x O y} = 30 °$ . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy

sao cho AB = 1. Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng:

A. $\frac{3}{2};$

B. $\sqrt{3};$

C. $2 \sqrt{2};$

D. 2.

Hiển thị đáp án

Đáp án đúng là: B

15 Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác (có đáp án) | Cánh diều Trắc nghiệm Toán 10

Theo định lí hàm sin, ta có:

$\frac{O B}{\sin \hat{O A B}} = \frac{A B}{\sin \hat{A O B}} \Leftrightarrow O B = \frac{A B}{\sin \hat{A O B}} . \sin \hat{O A B}$

$\Leftrightarrow \frac{1}{\sin 30 °} . \sin \hat{O A B} = 2 \sin \hat{O A B}$

Do đó, độ dài OB lớn nhất khi và chỉ khi: < $\sin \hat{O A B} = 1 \Leftrightarrow \hat{O A B} = 90 °$ .

Khi đó OB = 2.Tam giác OAB vuông tại $A \Rightarrow O A = \sqrt{O B^{2} - A B^{2}} = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$ .

Câu 13.Tam giác ABC có $A B = c, B C = a, C A = b$ . Các cạnh a, b, c liên hệ với nhau bởi đẳng thức $b (b^{2} - a^{2}) = c (a^{2} - c^{2})$ . Khi đó góc $\hat{B A C}$ bằng bao nhiêu độ?

A. $30 °;$

B. $45 °;$

C. $60 °;$

D. $90 ° .$

Hiển thị đáp án

Đáp án đúng là: C

Theo định lí hàm cosin, ta có: $\cos \hat{B A C} = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} = \frac{c^{2} + b^{2} - a^{2}}{2 b c}$

Mà $b (b^{2} - a^{2}) = c (a^{2} - c^{2})$ $\Leftrightarrow b^{3} - a^{2} b = a^{2} c - c^{3}$

$\Leftrightarrow - a^{2} (b + c) + (b^{3} + c^{3}) = 0$

$\Leftrightarrow (b + c) (b^{2} + c^{2} - a^{2} - b c) = 0$

$\Leftrightarrow b^{2} + c^{2} - a^{2} - b c = 0$ (do $b > 0, c > 0$ )

$\Leftrightarrow b^{2} + c^{2} - a^{2} = b c$

Khi đó, $\cos \hat{B A C} = \frac{b^{2} + c^{2} - a^{2}}{2 b c} = \frac{1}{2} \Rightarrow \hat{B A C} = 60 °$ .

Câu 14.Tam giác ABC vuông tại A, có $A B = c, A C = b$ . Gọi m là độ dài đoạn phân giác trong góc $\hat{B A C}$ . Tính m theo b và c.

A. $m = \frac{\sqrt{2} b c}{b + c};$

B. $m = \frac{2 (b + c)}{b c};$

C. $m = \frac{2 b c}{b + c};$

D. $m = \frac{\sqrt{2} (b + c)}{b c} .$

Hiển thị đáp án

Đáp án đúng là: A

Ta có: $B C = \sqrt{A B^{2} + A C^{2}} = \sqrt{b^{2} + c^{2}}$ .

Do AD là phân giác trong của $\hat{B A C}$

$\Rightarrow B D = \frac{A B}{A C} . D C = \frac{c}{b} . D C = \frac{c}{b + c} . B C = \frac{c \sqrt{b^{2} + c^{2}}}{b + c}$ .

Theo định lí hàm cosin, ta có:

$B D^{2} = A B^{2} + A D^{2} - 2. A B . A D . \cos \hat{A B D}$

$\Leftrightarrow \frac{c^{2} (b^{2} + c^{2})}{{(b + c)}^{2}} = c^{2} + A D^{2} - 2 c . A D . \cos 45 °$

$\Rightarrow A D^{2} - c \sqrt{2} . A D + (c^{2} - \frac{c^{2} (b^{2} + c^{2})}{{(b + c)}^{2}}) = 0$

$\Leftrightarrow A D^{2} - c \sqrt{2} . A D + \frac{2 b c^{3}}{{(b + c)}^{2}} = 0$

$\Rightarrow A D = \frac{\sqrt{2} b c}{b + c}$ hay $m = \frac{\sqrt{2} b c}{b + c}$ .

Câu 15. Tam giác ABC có BC = 10 và $\hat{A} = 30^{O}$ . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

A. R = 5;

B. R = 10;

C. $R = \frac{10}{\sqrt{3}};$

D. $R = 10 \sqrt{3} .$

Hiển thị đáp án

Đáp án đúng là: B

Áp dụng định lí sin, ta có: $\frac{B C}{\sin \hat{B A C}} = 2 R \Rightarrow R = \frac{B C}{2. \sin \hat{A}} = \frac{10}{2. \sin 30^{0}} = 10.$

Xem thêm bài tập trắc nghiệm Toán lớp 10 Cánh diều có đáp án hay khác:

Trắc nghiệm Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác

Trắc nghiệm Toán 10 Bài 3: Khái niệm vectơ

Trắc nghiệm Toán 10 Bài 4: Tổng và hiệu của hai vectơ

Trắc nghiệm Toán 10 Bài 5: Tích của một số với một vectơ

Trắc nghiệm Toán 10 Bài 6: Tích vô hướng của hai vectơ

1 403 04/01/2024

Mua tài liệu

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3